Less is More: Convergence Benefits of Fewer Data Weight Updates over Longer Horizon

Data mixing--the strategic reweighting of training domains--is a critical component in training robust machine learning models. This problem is naturally formulated as a bilevel optimization task, where the outer loop optimizes domain weights to minimize validation loss, and the inner loop optimizes model parameters to minimize the weighted training loss. Classical bilevel optimization relies on hypergradients, which theoretically require the inner optimization to reach convergence. However, due to computational constraints, state-of-the-art methods use a finite, often small, number of inner update steps before updating the weights. The theoretical implications of this approximation are not well understood. In this work, we rigorously analyze the convergence behavior of data mixing with a finite number of inner steps $T$. We prove that the "greedy" practical approach of using $T=1$ can fail even in a simple quadratic example. Under a fixed parameter update budget $N$ and assuming the per-domain losses are strongly convex, we show that the optimal $T$ scales as $Θ(\log N)$ (resp., $Θ({(N \log N)}^{1/2})$) for the data mixing problem with access to full (resp., stochastic) gradients. We complement our theoretical results with proof-of-concept experiments.

An Explainable Hybrid AI Framework for Enhanced Tuberculosis and Symptom Detection

Tuberculosis remains a critical global health issue, particularly in resource-limited and remote areas. Early detection is vital for treatment, yet the lack of skilled radiologists underscores the need for artificial intelligence (AI)-driven screening tools. Developing reliable AI models is challenging due to the necessity for large, high-quality datasets, which are costly to obtain. To tackle this, we propose a teacher--student framework which enhances both disease and symptom detection on chest X-rays by integrating two supervised heads and a self-supervised head. Our model achieves an accuracy of 98.85% for distinguishing between COVID-19, tuberculosis, and normal cases, and a macro-F1 score of 90.09% for multilabel symptom detection, significantly outperforming baselines. The explainability assessments also show the model bases its predictions on relevant anatomical features, demonstrating promise for deployment in clinical screening and triage settings.

Accelerating Retrieval-Augmented Generation

An evolving solution to address hallucination and enhance accuracy in large language models (LLMs) is Retrieval-Augmented Generation (RAG), which involves augmenting LLMs with information retrieved from an external knowledge source, such as the web. This paper profiles several RAG execution pipelines and demystifies the complex interplay between their retrieval and generation phases. We demonstrate that while exact retrieval schemes are expensive, they can reduce inference time compared to approximate retrieval variants because an exact retrieval model can send a smaller but more accurate list of documents to the generative model while maintaining the same end-to-end accuracy. This observation motivates the acceleration of the exact nearest neighbor search for RAG. In this work, we design Intelligent Knowledge Store (IKS), a type-2 CXL device that implements a scale-out near-memory acceleration architecture with a novel cache-coherent interface between the host CPU and near-memory accelerators. IKS offers 13.4-27.9x faster exact nearest neighbor search over a 512GB vector database compared with executing the search on Intel Sapphire Rapids CPUs. This higher search performance translates to 1.7-26.3x lower end-to-end inference time for representative RAG applications. IKS is inherently a memory expander; its internal DRAM can be disaggregated and used for other applications running on the server to prevent DRAM, which is the most expensive component in today's servers, from being stranded.

Empowering Tuberculosis Screening with Explainable Self-Supervised Deep Neural Networks

Tuberculosis persists as a global health crisis, especially in resource-limited populations and remote regions, with more than 10 million individuals newly infected annually. It stands as a stark symbol of inequity in public health. Tuberculosis impacts roughly a quarter of the global populace, with the majority of cases concentrated in eight countries, accounting for two-thirds of all tuberculosis infections. Although a severe ailment, tuberculosis is both curable and manageable. However, early detection and screening of at-risk populations are imperative. Chest x-ray stands as the predominant imaging technique utilized in tuberculosis screening efforts. However, x-ray screening necessitates skilled radiologists, a resource often scarce, particularly in remote regions with limited resources. Consequently, there is a pressing need for artificial intelligence (AI)-powered systems to support clinicians and healthcare providers in swift screening. However, training a reliable AI model necessitates large-scale high-quality data, which can be difficult and costly to acquire. Inspired by these challenges, in this work, we introduce an explainable self-supervised self-train learning network tailored for tuberculosis case screening. The network achieves an outstanding overall accuracy of 98.14% and demonstrates high recall and precision rates of 95.72% and 99.44%, respectively, in identifying tuberculosis cases, effectively capturing clinically significant features.

The Price is Right: Learning Market Equilibria from Samples

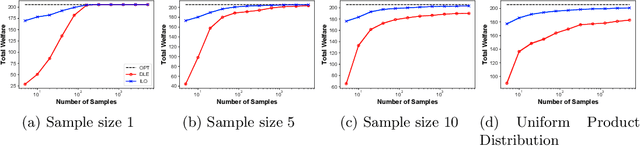
Equilibrium computation in markets usually considers settings where player valuation functions are known. We consider the setting where player valuations are unknown; using a PAC learning-theoretic framework, we analyze some classes of common valuation functions, and provide algorithms which output direct PAC equilibrium allocations, not estimates based on attempting to learn valuation functions. Since there exist trivial PAC market outcomes with an unbounded worst-case efficiency loss, we lower-bound the efficiency of our algorithms. While the efficiency loss under general distributions is rather high, we show that in some cases (e.g., unit-demand valuations), it is possible to find a PAC market equilibrium with significantly better utility.

Model Explanations with Differential Privacy

Black-box machine learning models are used in critical decision-making domains, giving rise to several calls for more algorithmic transparency. The drawback is that model explanations can leak information about the training data and the explanation data used to generate them, thus undermining data privacy. To address this issue, we propose differentially private algorithms to construct feature-based model explanations. We design an adaptive differentially private gradient descent algorithm, that finds the minimal privacy budget required to produce accurate explanations. It reduces the overall privacy loss on explanation data, by adaptively reusing past differentially private explanations. It also amplifies the privacy guarantees with respect to the training data. We evaluate the implications of differentially private models and our privacy mechanisms on the quality of model explanations.

High Dimensional Model Explanations: an Axiomatic Approach

Complex black-box machine learning models are regularly used in critical decision-making domains. This has given rise to several calls for algorithmic explainability. Many explanation algorithms proposed in literature assign importance to each feature individually. However, such explanations fail to capture the joint effects of sets of features. Indeed, few works so far formally analyze \coloremph{high dimensional model explanations}. In this paper, we propose a novel high dimension model explanation method that captures the joint effect of feature subsets. We propose a new axiomatization for a generalization of the Banzhaf index; our method can also be thought of as an approximation of a black-box model by a higher-order polynomial. In other words, this work justifies the use of the generalized Banzhaf index as a model explanation by showing that it uniquely satisfies a set of natural desiderata and that it is the optimal local approximation of a black-box model. Our empirical evaluation of our measure highlights how it manages to capture desirable behavior, whereas other measures that do not satisfy our axioms behave in an unpredictable manner.