The Price is Right: Learning Market Equilibria from Samples

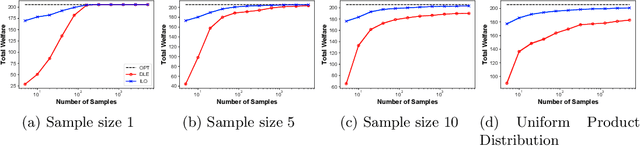
Equilibrium computation in markets usually considers settings where player valuation functions are known. We consider the setting where player valuations are unknown; using a PAC learning-theoretic framework, we analyze some classes of common valuation functions, and provide algorithms which output direct PAC equilibrium allocations, not estimates based on attempting to learn valuation functions. Since there exist trivial PAC market outcomes with an unbounded worst-case efficiency loss, we lower-bound the efficiency of our algorithms. While the efficiency loss under general distributions is rather high, we show that in some cases (e.g., unit-demand valuations), it is possible to find a PAC market equilibrium with significantly better utility.