Linear Projections of Teacher Embeddings for Few-Class Distillation

Knowledge Distillation (KD) has emerged as a promising approach for transferring knowledge from a larger, more complex teacher model to a smaller student model. Traditionally, KD involves training the student to mimic the teacher's output probabilities, while more advanced techniques have explored guiding the student to adopt the teacher's internal representations. Despite its widespread success, the performance of KD in binary classification and few-class problems has been less satisfactory. This is because the information about the teacher model's generalization patterns scales directly with the number of classes. Moreover, several sophisticated distillation methods may not be universally applicable or effective for data types beyond Computer Vision. Consequently, effective distillation techniques remain elusive for a range of key real-world applications, such as sentiment analysis, search query understanding, and advertisement-query relevance assessment. Taking these observations into account, we introduce a novel method for distilling knowledge from the teacher's model representations, which we term Learning Embedding Linear Projections (LELP). Inspired by recent findings about the structure of final-layer representations, LELP works by identifying informative linear subspaces in the teacher's embedding space, and splitting them into pseudo-subclasses. The student model is then trained to replicate these pseudo-classes. Our experimental evaluation on large-scale NLP benchmarks like Amazon Reviews and Sentiment140 demonstrate the LELP is consistently competitive with, and typically superior to, existing state-of-the-art distillation algorithms for binary and few-class problems, where most KD methods suffer.

Leveraging Low-Rank and Sparse Recurrent Connectivity for Robust Closed-Loop Control

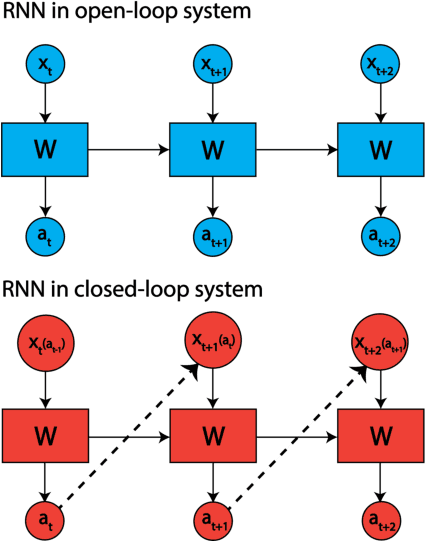
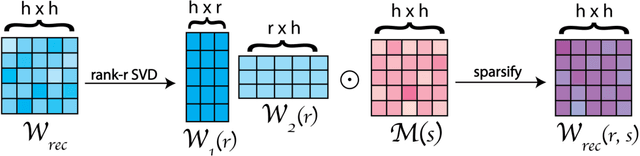
Developing autonomous agents that can interact with changing environments is an open challenge in machine learning. Robustness is particularly important in these settings as agents are often fit offline on expert demonstrations but deployed online where they must generalize to the closed feedback loop within the environment. In this work, we explore the application of recurrent neural networks to tasks of this nature and understand how a parameterization of their recurrent connectivity influences robustness in closed-loop settings. Specifically, we represent the recurrent connectivity as a function of rank and sparsity and show both theoretically and empirically that modulating these two variables has desirable effects on network dynamics. The proposed low-rank, sparse connectivity induces an interpretable prior on the network that proves to be most amenable for a class of models known as closed-form continuous-time neural networks (CfCs). We find that CfCs with fewer parameters can outperform their full-rank, fully-connected counterparts in the online setting under distribution shift. This yields memory-efficient and robust agents while opening a new perspective on how we can modulate network dynamics through connectivity.

On the Size and Approximation Error of Distilled Sets

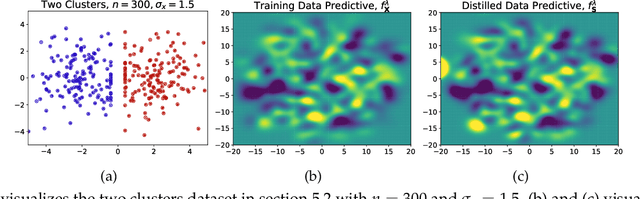
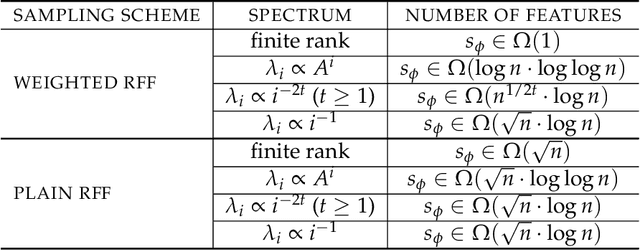
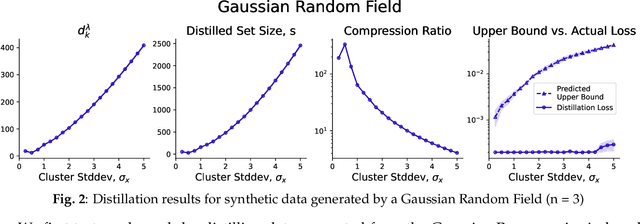
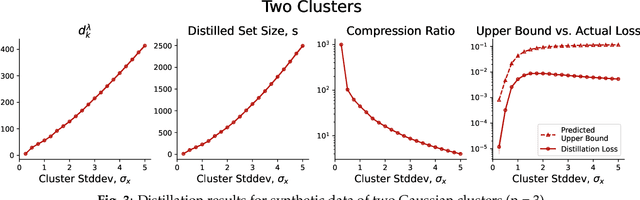
Dataset Distillation is the task of synthesizing small datasets from large ones while still retaining comparable predictive accuracy to the original uncompressed dataset. Despite significant empirical progress in recent years, there is little understanding of the theoretical limitations/guarantees of dataset distillation, specifically, what excess risk is achieved by distillation compared to the original dataset, and how large are distilled datasets? In this work, we take a theoretical view on kernel ridge regression (KRR) based methods of dataset distillation such as Kernel Inducing Points. By transforming ridge regression in random Fourier features (RFF) space, we provide the first proof of the existence of small (size) distilled datasets and their corresponding excess risk for shift-invariant kernels. We prove that a small set of instances exists in the original input space such that its solution in the RFF space coincides with the solution of the original data. We further show that a KRR solution can be generated using this distilled set of instances which gives an approximation towards the KRR solution optimized on the full input data. The size of this set is linear in the dimension of the RFF space of the input set or alternatively near linear in the number of effective degrees of freedom, which is a function of the kernel, number of datapoints, and the regularization parameter $\lambda$. The error bound of this distilled set is also a function of $\lambda$. We verify our bounds analytically and empirically.

Dataset Distillation with Convexified Implicit Gradients

We propose a new dataset distillation algorithm using reparameterization and convexification of implicit gradients (RCIG), that substantially improves the state-of-the-art. To this end, we first formulate dataset distillation as a bi-level optimization problem. Then, we show how implicit gradients can be effectively used to compute meta-gradient updates. We further equip the algorithm with a convexified approximation that corresponds to learning on top of a frozen finite-width neural tangent kernel. Finally, we improve bias in implicit gradients by parameterizing the neural network to enable analytical computation of final-layer parameters given the body parameters. RCIG establishes the new state-of-the-art on a diverse series of dataset distillation tasks. Notably, with one image per class, on resized ImageNet, RCIG sees on average a 108% improvement over the previous state-of-the-art distillation algorithm. Similarly, we observed a 66% gain over SOTA on Tiny-ImageNet and 37% on CIFAR-100.

Dataset Distillation Fixes Dataset Reconstruction Attacks

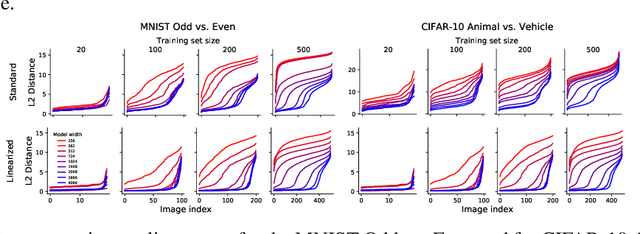
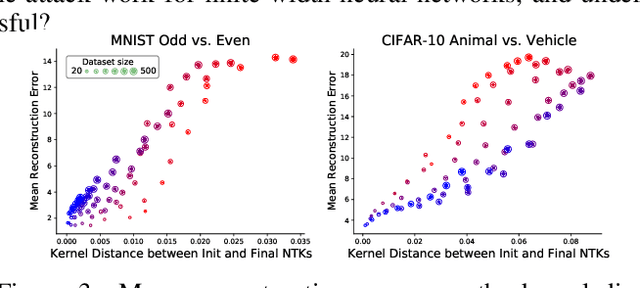
Modern deep learning requires large volumes of data, which could contain sensitive or private information which cannot be leaked. Recent work has shown for homogeneous neural networks a large portion of this training data could be reconstructed with only access to the trained network parameters. While the attack was shown to work empirically, there exists little formal understanding of its effectiveness regime, and ways to defend against it. In this work, we first build a stronger version of the dataset reconstruction attack and show how it can provably recover its entire training set in the infinite width regime. We then empirically study the characteristics of this attack on two-layer networks and reveal that its success heavily depends on deviations from the frozen infinite-width Neural Tangent Kernel limit. More importantly, we formally show for the first time that dataset reconstruction attacks are a variation of dataset distillation. This key theoretical result on the unification of dataset reconstruction and distillation not only sheds more light on the characteristics of the attack but enables us to design defense mechanisms against them via distillation algorithms.

Generalized Variational Continual Learning

Continual learning deals with training models on new tasks and datasets in an online fashion. One strand of research has used probabilistic regularization for continual learning, with two of the main approaches in this vein being Online Elastic Weight Consolidation (Online EWC) and Variational Continual Learning (VCL). VCL employs variational inference, which in other settings has been improved empirically by applying likelihood-tempering. We show that applying this modification to VCL recovers Online EWC as a limiting case, allowing for interpolation between the two approaches. We term the general algorithm Generalized VCL (GVCL). In order to mitigate the observed overpruning effect of VI, we take inspiration from a common multi-task architecture, neural networks with task-specific FiLM layers, and find that this addition leads to significant performance gains, specifically for variational methods. In the small-data regime, GVCL strongly outperforms existing baselines. In larger datasets, GVCL with FiLM layers outperforms or is competitive with existing baselines in terms of accuracy, whilst also providing significantly better calibration.