Dataset Distillation Fixes Dataset Reconstruction Attacks

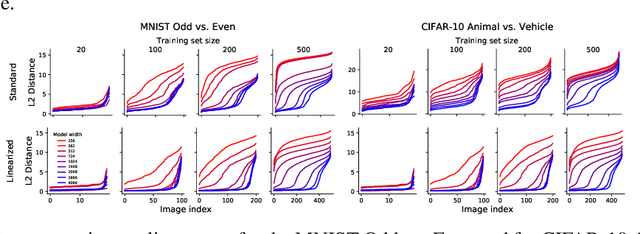
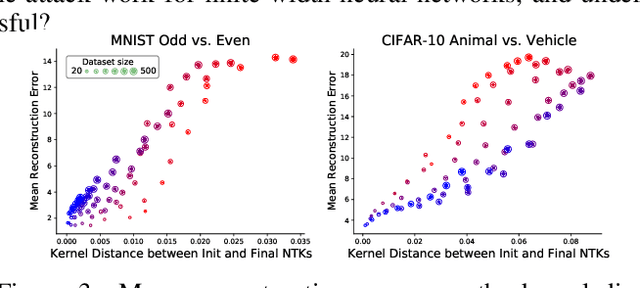
Modern deep learning requires large volumes of data, which could contain sensitive or private information which cannot be leaked. Recent work has shown for homogeneous neural networks a large portion of this training data could be reconstructed with only access to the trained network parameters. While the attack was shown to work empirically, there exists little formal understanding of its effectiveness regime, and ways to defend against it. In this work, we first build a stronger version of the dataset reconstruction attack and show how it can provably recover its entire training set in the infinite width regime. We then empirically study the characteristics of this attack on two-layer networks and reveal that its success heavily depends on deviations from the frozen infinite-width Neural Tangent Kernel limit. More importantly, we formally show for the first time that dataset reconstruction attacks are a variation of dataset distillation. This key theoretical result on the unification of dataset reconstruction and distillation not only sheds more light on the characteristics of the attack but enables us to design defense mechanisms against them via distillation algorithms.