Autonomous Field-of-View Adjustment Using Adaptive Kinematic Constrained Control with Robot-Held Microscopic Camera Feedback

Robotic systems for manipulation in millimeter scale often use a camera with high magnification for visual feedback of the target region. However, the limited field-of-view (FoV) of the microscopic camera necessitates camera motion to capture a broader workspace environment. In this work, we propose an autonomous robotic control method to constrain a robot-held camera within a designated FoV. Furthermore, we model the camera extrinsics as part of the kinematic model and use camera measurements coupled with a U-Net based tool tracking to adapt the complete robotic model during task execution. As a proof-of-concept demonstration, the proposed framework was evaluated in a bi-manual setup, where the microscopic camera was controlled to view a tool moving in a pre-defined trajectory. The proposed method allowed the camera to stay 99.5% of the time within the real FoV, compared to 48.1% without the proposed adaptive control.

Vitreoretinal Surgical Robotic System with Autonomous Orbital Manipulation using Vector-Field Inequalities

Vitreoretinal surgery pertains to the treatment of delicate tissues on the fundus of the eye using thin instruments. Surgeons frequently rotate the eye during surgery, which is called orbital manipulation, to observe regions around the fundus without moving the patient. In this paper, we propose the autonomous orbital manipulation of the eye in robot-assisted vitreoretinal surgery with our tele-operated surgical system. In a simulation study, we preliminarily investigated the increase in the manipulability of our system using orbital manipulation. Furthermore, we demonstrated the feasibility of our method in experiments with a physical robot and a realistic eye model, showing an increase in the view-able area of the fundus when compared to a conventional technique. Source code and minimal example available at https://github.com/mmmarinho/icra2023_orbitalmanipulation.

Adaptive Constrained Kinematic Control using Partial or Complete Task-Space Measurements

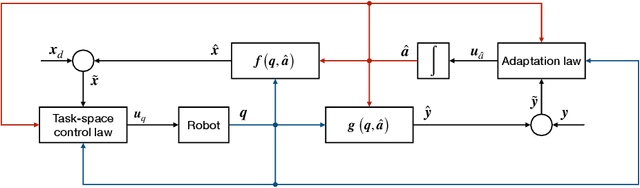
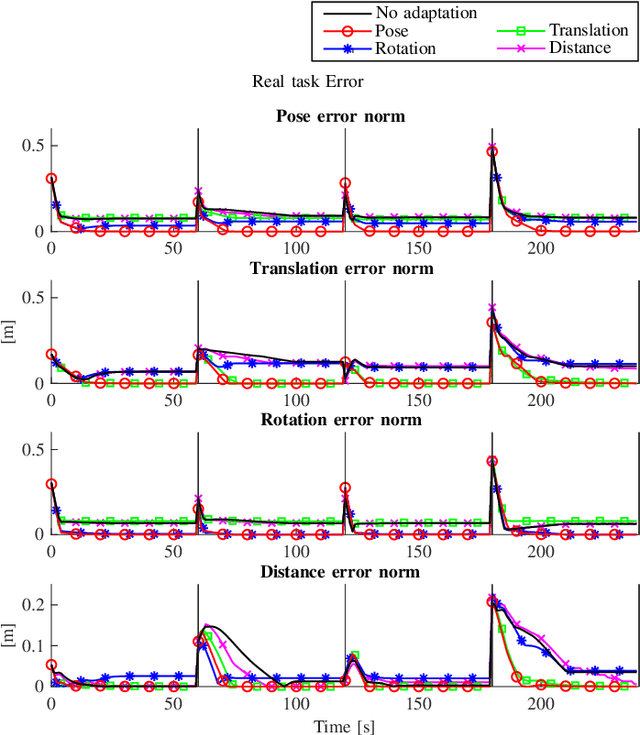
Recent advancements in constrained kinematic control make it an attractive strategy for controlling robots with arbitrary geometry in challenging tasks. Most current works assume that the robot kinematic model is precise enough for the task at hand. However, with increasing demands and safety requirements in robotic applications, there is a need for a controller that compensates online for kinematic inaccuracies. We propose an adaptive constrained kinematic control strategy based on quadratic programming, which uses partial or complete task-space measurements to compensate online for calibration errors. Our method is validated in experiments and simulations that show increased accuracy and safety compared to a state-of-the-art kinematic control strategy.

MBAPose: Mask and Bounding-Box Aware Pose Estimation of Surgical Instruments with Photorealistic Domain Randomization

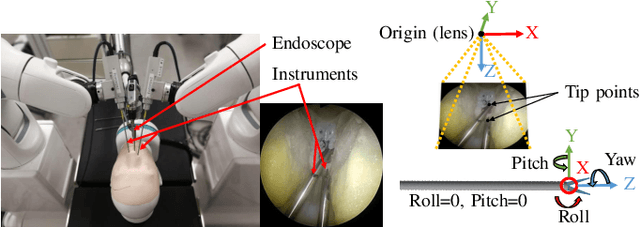
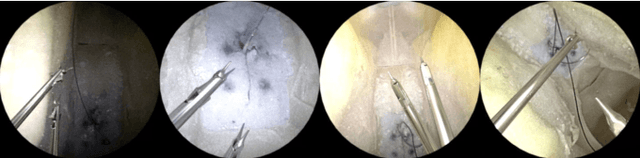
Surgical robots are controlled using a priori models based on robots' geometric parameters, which are calibrated before the surgical procedure. One of the challenges in using robots in real surgical settings is that parameters change over time, consequently deteriorating control accuracy. In this context, our group has been investigating online calibration strategies without added sensors. In one step toward that goal, we have developed an algorithm to estimate the pose of the instruments' shafts in endoscopic images. In this study, we build upon that earlier work and propose a new framework to more precisely estimate the pose of a rigid surgical instrument. Our strategy is based on a novel pose estimation model called MBAPose and the use of synthetic training data. Our experiments demonstrated an improvement of 21 % for translation error and 26 % for orientation error on synthetic test data with respect to our previous work. Results with real test data provide a baseline for further research.

DQ Robotics: a Library for Robot Modeling and Control Using Dual Quaternion Algebra

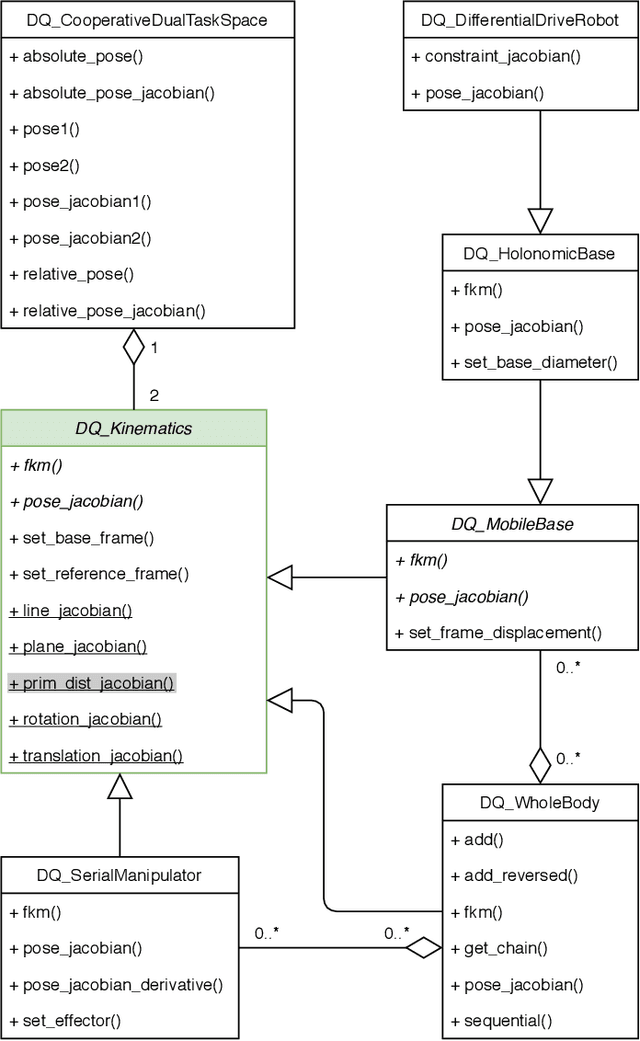
Dual quaternion algebra and its application to robotics have gained considerable interest in the last two decades. Dual quaternions have great geometric appeal and easily capture physical phenomena inside an algebraic framework that is useful for both robot modeling and control. Mathematical objects, such as points, lines, planes, infinite cylinders, spheres, coordinate systems, twists, and wrenches are all well defined as dual quaternions. Therefore, simple operators are used to represent those objects in different frames and operations such as inner products and cross products are used to extract useful geometric relationships between them. Nonetheless, the dual quaternion algebra is not widespread as it could be, mostly because efficient and easy-to-use computational tools are not abundant and usually are restricted to the particular algebra of quaternions. To bridge this gap between theory and implementation, this paper introduces DQ Robotics, a library for robot modeling and control using dual quaternion algebra that is easy to use and intuitive enough to be used for self-study and education while being computationally efficient for deployment on real applications.

Virtual Fixture Assistance for Suturing in Robot-Aided Pediatric Endoscopic Surgery

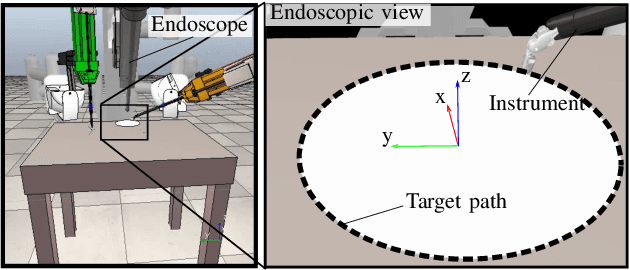
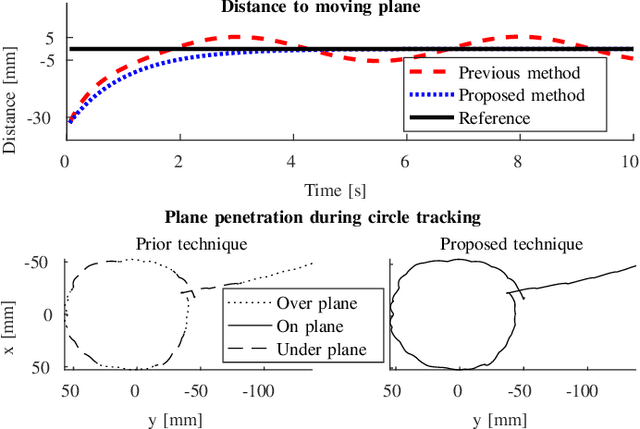
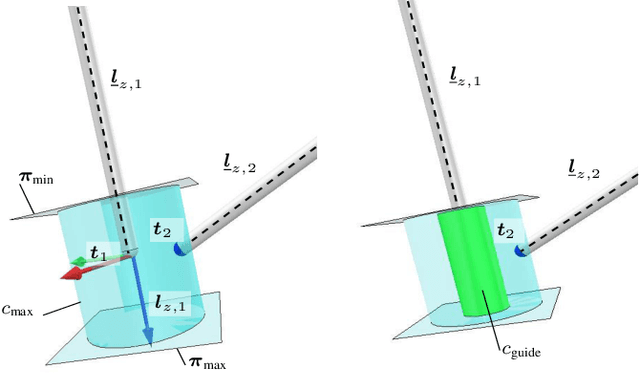
The limited workspace in pediatric endoscopic surgery makes surgical suturing one of the most difficult tasks. During suturing, surgeons have to prevent collisions between tools and also collisions with the surrounding tissues. Surgical robots have been shown to be effective in adult laparoscopy, but assistance for suturing in constrained workspaces has not been yet fully explored. In this letter, we propose guidance virtual fixtures to enhance the performance and the safety of suturing while generating the required task constraints using constrained optimization and Cartesian force feedback. We propose two guidance methods: looping virtual fixtures and a trajectory guidance cylinder, that are based on dynamic geometric elements. In simulations and experiments with a physical robot, we show that the proposed methods achieve a more precise and safer looping in robot-assisted pediatric endoscopy.