What classifiers know what they don't?

Being uncertain when facing the unknown is key to intelligent decision making. However, machine learning algorithms lack reliable estimates about their predictive uncertainty. This leads to wrong and overly-confident decisions when encountering classes unseen during training. Despite the importance of equipping classifiers with uncertainty estimates ready for the real world, prior work has focused on small datasets and little or no class discrepancy between training and testing data. To close this gap, we introduce UIMNET: a realistic, ImageNet-scale test-bed to evaluate predictive uncertainty estimates for deep image classifiers. Our benchmark provides implementations of eight state-of-the-art algorithms, six uncertainty measures, four in-domain metrics, three out-domain metrics, and a fully automated pipeline to train, calibrate, ensemble, select, and evaluate models. Our test-bed is open-source and all of our results are reproducible from a fixed commit in our repository. Adding new datasets, algorithms, measures, or metrics is a matter of a few lines of code-in so hoping that UIMNET becomes a stepping stone towards realistic, rigorous, and reproducible research in uncertainty estimation. Our results show that ensembles of ERM classifiers as well as single MIMO classifiers are the two best alternatives currently available to measure uncertainty about both in-domain and out-domain classes.

Learning about an exponential amount of conditional distributions

We introduce the Neural Conditioner (NC), a self-supervised machine able to learn about all the conditional distributions of a random vector $X$. The NC is a function $NC(x \cdot a, a, r)$ that leverages adversarial training to match each conditional distribution $P(X_r|X_a=x_a)$. After training, the NC generalizes to sample from conditional distributions never seen, including the joint distribution. The NC is also able to auto-encode examples, providing data representations useful for downstream classification tasks. In sum, the NC integrates different self-supervised tasks (each being the estimation of a conditional distribution) and levels of supervision (partially observed data) seamlessly into a single learning experience.

MINE: Mutual Information Neural Estimation

We argue that the estimation of mutual information between high dimensional continuous random variables can be achieved by gradient descent over neural networks. We present a Mutual Information Neural Estimator (MINE) that is linearly scalable in dimensionality as well as in sample size, trainable through back-prop, and strongly consistent. We present a handful of applications on which MINE can be used to minimize or maximize mutual information. We apply MINE to improve adversarially trained generative models. We also use MINE to implement Information Bottleneck, applying it to supervised classification; our results demonstrate substantial improvement in flexibility and performance in these settings.

Hierarchical Adversarially Learned Inference

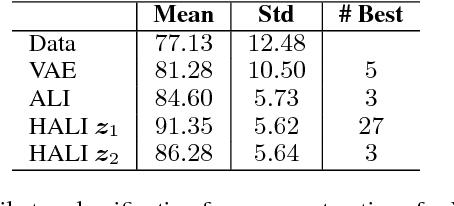
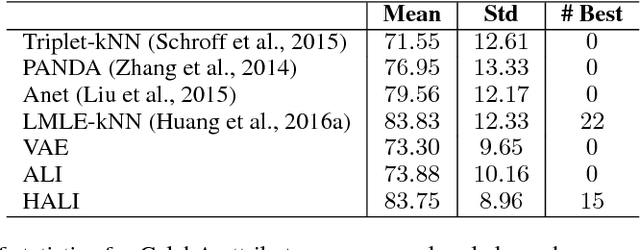
We propose a novel hierarchical generative model with a simple Markovian structure and a corresponding inference model. Both the generative and inference model are trained using the adversarial learning paradigm. We demonstrate that the hierarchical structure supports the learning of progressively more abstract representations as well as providing semantically meaningful reconstructions with different levels of fidelity. Furthermore, we show that minimizing the Jensen-Shanon divergence between the generative and inference network is enough to minimize the reconstruction error. The resulting semantically meaningful hierarchical latent structure discovery is exemplified on the CelebA dataset. There, we show that the features learned by our model in an unsupervised way outperform the best handcrafted features. Furthermore, the extracted features remain competitive when compared to several recent deep supervised approaches on an attribute prediction task on CelebA. Finally, we leverage the model's inference network to achieve state-of-the-art performance on a semi-supervised variant of the MNIST digit classification task.