Misha Dashevskiy
The CLRS Algorithmic Reasoning Benchmark
Jun 04, 2022



Abstract:Learning representations of algorithms is an emerging area of machine learning, seeking to bridge concepts from neural networks with classical algorithms. Several important works have investigated whether neural networks can effectively reason like algorithms, typically by learning to execute them. The common trend in the area, however, is to generate targeted kinds of algorithmic data to evaluate specific hypotheses, making results hard to transfer across publications, and increasing the barrier of entry. To consolidate progress and work towards unified evaluation, we propose the CLRS Algorithmic Reasoning Benchmark, covering classical algorithms from the Introduction to Algorithms textbook. Our benchmark spans a variety of algorithmic reasoning procedures, including sorting, searching, dynamic programming, graph algorithms, string algorithms and geometric algorithms. We perform extensive experiments to demonstrate how several popular algorithmic reasoning baselines perform on these tasks, and consequently, highlight links to several open challenges. Our library is readily available at https://github.com/deepmind/clrs.
Formalising Concepts as Grounded Abstractions
Jan 13, 2021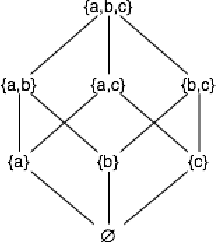
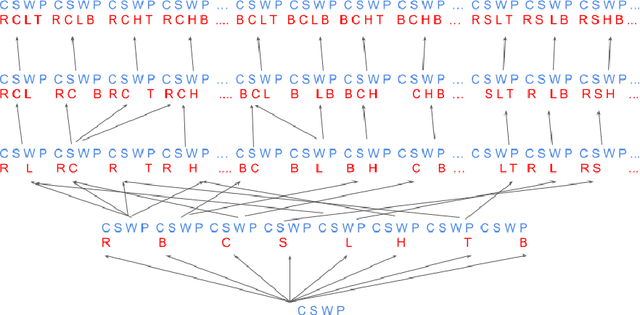
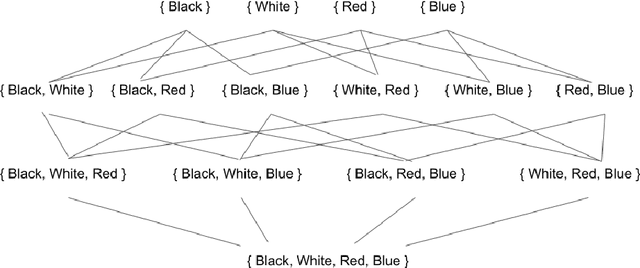
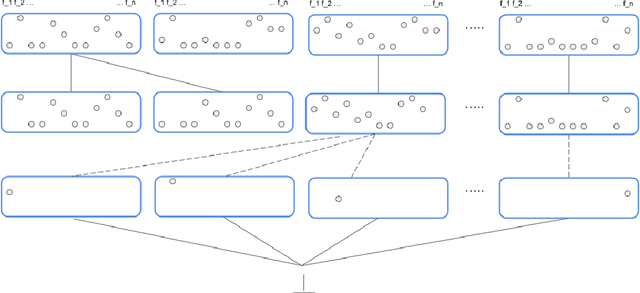
Abstract:The notion of concept has been studied for centuries, by philosophers, linguists, cognitive scientists, and researchers in artificial intelligence (Margolis & Laurence, 1999). There is a large literature on formal, mathematical models of concepts, including a whole sub-field of AI -- Formal Concept Analysis -- devoted to this topic (Ganter & Obiedkov, 2016). Recently, researchers in machine learning have begun to investigate how methods from representation learning can be used to induce concepts from raw perceptual data (Higgins, Sonnerat, et al., 2018). The goal of this report is to provide a formal account of concepts which is compatible with this latest work in deep learning. The main technical goal of this report is to show how techniques from representation learning can be married with a lattice-theoretic formulation of conceptual spaces. The mathematics of partial orders and lattices is a standard tool for modelling conceptual spaces (Ch.2, Mitchell (1997), Ganter and Obiedkov (2016)); however, there is no formal work that we are aware of which defines a conceptual lattice on top of a representation that is induced using unsupervised deep learning (Goodfellow et al., 2016). The advantages of partially-ordered lattice structures are that these provide natural mechanisms for use in concept discovery algorithms, through the meets and joins of the lattice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge