ReSCORE: Label-free Iterative Retriever Training for Multi-hop Question Answering with Relevance-Consistency Supervision

Multi-hop question answering (MHQA) involves reasoning across multiple documents to answer complex questions. Dense retrievers typically outperform sparse methods like BM25 by leveraging semantic embeddings; however, they require labeled query-document pairs for fine-tuning. This poses a significant challenge in MHQA due to the high variability of queries (reformulated) questions throughout the reasoning steps. To overcome this limitation, we introduce Retriever Supervision with Consistency and Relevance (ReSCORE), a novel method for training dense retrievers for MHQA without labeled documents. ReSCORE leverages large language models to capture each documents relevance to the question and consistency with the correct answer and use them to train a retriever within an iterative question-answering framework. Experiments on three MHQA benchmarks demonstrate the effectiveness of ReSCORE, with significant improvements in retrieval, and in turn, the state-of-the-art MHQA performance. Our implementation is available at: https://leeds1219.github.io/ReSCORE.

Model Merging is Secretly Certifiable: Non-Vacuous Generalisation Bounds for Low-Shot Learning

Certifying the IID generalisation ability of deep networks is the first of many requirements for trusting AI in high-stakes applications from medicine to security. However, when instantiating generalisation bounds for deep networks it remains challenging to obtain non-vacuous guarantees, especially when applying contemporary large models on the small scale data prevalent in such high-stakes fields. In this paper, we draw a novel connection between a family of learning methods based on model fusion and generalisation certificates, and surprisingly show that with minor adjustment several existing learning strategies already provide non-trivial generalisation guarantees. Essentially, by focusing on data-driven learning of downstream tasks by fusion rather than fine-tuning, the certified generalisation gap becomes tiny and independent of the base network size, facilitating its certification. Our results show for the first time non-trivial generalisation guarantees for learning with as low as 100 examples, while using vision models such as VIT-B and language models such as mistral-7B. This observation is significant as it has immediate implications for facilitating the certification of existing systems as trustworthy, and opens up new directions for research at the intersection of practice and theory.

A Unified Framework for Diffusion Bridge Problems: Flow Matching and Schrödinger Matching into One

The bridge problem is to find an SDE (or sometimes an ODE) that bridges two given distributions. The application areas of the bridge problem are enormous, among which the recent generative modeling (e.g., conditional or unconditional image generation) is the most popular. Also the famous Schr\"{o}dinger bridge problem, a widely known problem for a century, is a special instance of the bridge problem. Two most popular algorithms to tackle the bridge problems in the deep learning era are: (conditional) flow matching and iterative fitting algorithms, where the former confined to ODE solutions, and the latter specifically for the Schr\"{o}dinger bridge problem. The main contribution of this article is in two folds: i) We provide concise reviews of these algorithms with technical details to some extent; ii) We propose a novel unified perspective and framework that subsumes these seemingly unrelated algorithms (and their variants) into one. In particular, we show that our unified framework can instantiate the Flow Matching (FM) algorithm, the (mini-batch) optimal transport FM algorithm, the (mini-batch) Schr\"{o}dinger bridge FM algorithm, and the deep Schr\"{o}dinger bridge matching (DSBM) algorithm as its special cases. We believe that this unified framework will be useful for viewing the bridge problems in a more general and flexible perspective, and in turn can help researchers and practitioners to develop new bridge algorithms in their fields.

Model Diffusion for Certifiable Few-shot Transfer Learning

In modern large-scale deep learning, a prevalent and effective workflow for solving low-data problems is adapting powerful pre-trained foundation models (FMs) to new tasks via parameter-efficient fine-tuning (PEFT). However, while empirically effective, the resulting solutions lack generalisation guarantees to certify their accuracy - which may be required for ethical or legal reasons prior to deployment in high-importance applications. In this paper we develop a novel transfer learning approach that is designed to facilitate non-vacuous learning theoretic generalisation guarantees for downstream tasks, even in the low-shot regime. Specifically, we first use upstream tasks to train a distribution over PEFT parameters. We then learn the downstream task by a sample-and-evaluate procedure -- sampling plausible PEFTs from the trained diffusion model and selecting the one with the highest likelihood on the downstream data. Crucially, this confines our model hypothesis to a finite set of PEFT samples. In contrast to learning in the typical continuous hypothesis spaces of neural network weights, this facilitates tighter risk certificates. We instantiate our bound and show non-trivial generalization guarantees compared to existing learning approaches which lead to vacuous bounds in the low-shot regime.

FedP$^2$EFT: Federated Learning to Personalize Parameter Efficient Fine-Tuning for Multilingual LLMs

Federated learning (FL) has enabled the training of multilingual large language models (LLMs) on diverse and decentralized multilingual data, especially on low-resource languages. To improve client-specific performance, personalization via the use of parameter-efficient fine-tuning (PEFT) modules such as LoRA is common. This involves a personalization strategy (PS), such as the design of the PEFT adapter structures (e.g., in which layers to add LoRAs and what ranks) and choice of hyperparameters (e.g., learning rates) for fine-tuning. Instead of manual PS configuration, we propose FedP$^2$EFT, a federated learning-to-personalize method for multilingual LLMs in cross-device FL settings. Unlike most existing PEFT structure selection methods, which are prone to overfitting low-data regimes, FedP$^2$EFT collaboratively learns the optimal personalized PEFT structure for each client via Bayesian sparse rank selection. Evaluations on both simulated and real-world multilingual FL benchmarks demonstrate that FedP$^2$EFT largely outperforms existing personalized fine-tuning methods, while complementing a range of existing FL methods.

A Bayesian Approach to Data Point Selection

Data point selection (DPS) is becoming a critical topic in deep learning due to the ease of acquiring uncurated training data compared to the difficulty of obtaining curated or processed data. Existing approaches to DPS are predominantly based on a bi-level optimisation (BLO) formulation, which is demanding in terms of memory and computation, and exhibits some theoretical defects regarding minibatches. Thus, we propose a novel Bayesian approach to DPS. We view the DPS problem as posterior inference in a novel Bayesian model where the posterior distributions of the instance-wise weights and the main neural network parameters are inferred under a reasonable prior and likelihood model. We employ stochastic gradient Langevin MCMC sampling to learn the main network and instance-wise weights jointly, ensuring convergence even with minibatches. Our update equation is comparable to the widely used SGD and much more efficient than existing BLO-based methods. Through controlled experiments in both the vision and language domains, we present the proof-of-concept. Additionally, we demonstrate that our method scales effectively to large language models and facilitates automated per-task optimization for instruction fine-tuning datasets.

A Stochastic Approach to Bi-Level Optimization for Hyperparameter Optimization and Meta Learning

We tackle the general differentiable meta learning problem that is ubiquitous in modern deep learning, including hyperparameter optimization, loss function learning, few-shot learning, invariance learning and more. These problems are often formalized as Bi-Level optimizations (BLO). We introduce a novel perspective by turning a given BLO problem into a stochastic optimization, where the inner loss function becomes a smooth probability distribution, and the outer loss becomes an expected loss over the inner distribution. To solve this stochastic optimization, we adopt Stochastic Gradient Langevin Dynamics (SGLD) MCMC to sample inner distribution, and propose a recurrent algorithm to compute the MC-estimated hypergradient. Our derivation is similar to forward-mode differentiation, but we introduce a new first-order approximation that makes it feasible for large models without needing to store huge Jacobian matrices. The main benefits are two-fold: i) Our stochastic formulation takes into account uncertainty, which makes the method robust to suboptimal inner optimization or non-unique multiple inner minima due to overparametrization; ii) Compared to existing methods that often exhibit unstable behavior and hyperparameter sensitivity in practice, our method leads to considerably more reliable solutions. We demonstrate that the new approach achieves promising results on diverse meta learning problems and easily scales to learning 87M hyperparameters in the case of Vision Transformers.

FedL2P: Federated Learning to Personalize

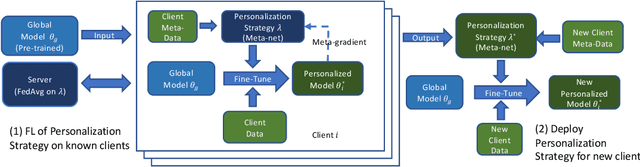
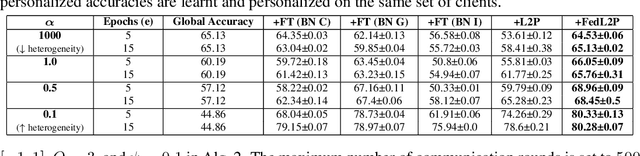
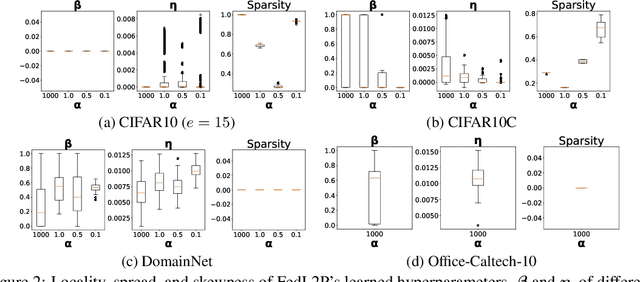
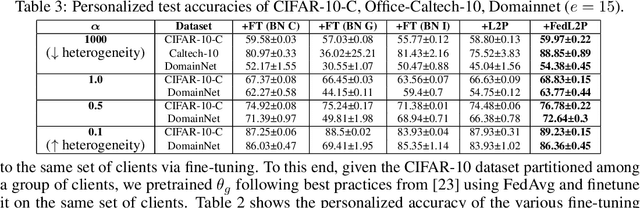
Federated learning (FL) research has made progress in developing algorithms for distributed learning of global models, as well as algorithms for local personalization of those common models to the specifics of each client's local data distribution. However, different FL problems may require different personalization strategies, and it may not even be possible to define an effective one-size-fits-all personalization strategy for all clients: depending on how similar each client's optimal predictor is to that of the global model, different personalization strategies may be preferred. In this paper, we consider the federated meta-learning problem of learning personalization strategies. Specifically, we consider meta-nets that induce the batch-norm and learning rate parameters for each client given local data statistics. By learning these meta-nets through FL, we allow the whole FL network to collaborate in learning a customized personalization strategy for each client. Empirical results show that this framework improves on a range of standard hand-crafted personalization baselines in both label and feature shift situations.

BayesDLL: Bayesian Deep Learning Library

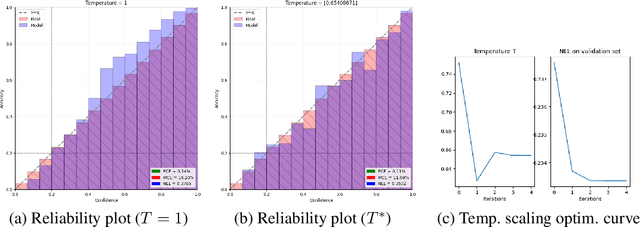
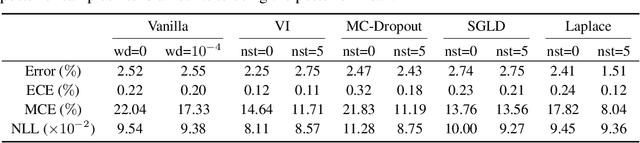
We release a new Bayesian neural network library for PyTorch for large-scale deep networks. Our library implements mainstream approximate Bayesian inference algorithms: variational inference, MC-dropout, stochastic-gradient MCMC, and Laplace approximation. The main differences from other existing Bayesian neural network libraries are as follows: 1) Our library can deal with very large-scale deep networks including Vision Transformers (ViTs). 2) We need virtually zero code modifications for users (e.g., the backbone network definition codes do not neet to be modified at all). 3) Our library also allows the pre-trained model weights to serve as a prior mean, which is very useful for performing Bayesian inference with the large-scale foundation models like ViTs that are hard to optimise from scratch with the downstream data alone. Our code is publicly available at: \url{https://github.com/SamsungLabs/BayesDLL}\footnote{A mirror repository is also available at: \url{https://github.com/minyoungkim21/BayesDLL}.}.

A Hierarchical Bayesian Model for Deep Few-Shot Meta Learning

We propose a novel hierarchical Bayesian model for learning with a large (possibly infinite) number of tasks/episodes, which suits well the few-shot meta learning problem. We consider episode-wise random variables to model episode-specific target generative processes, where these local random variables are governed by a higher-level global random variate. The global variable helps memorize the important information from historic episodes while controlling how much the model needs to be adapted to new episodes in a principled Bayesian manner. Within our model framework, the prediction on a novel episode/task can be seen as a Bayesian inference problem. However, a main obstacle in learning with a large/infinite number of local random variables in online nature, is that one is not allowed to store the posterior distribution of the current local random variable for frequent future updates, typical in conventional variational inference. We need to be able to treat each local variable as a one-time iterate in the optimization. We propose a Normal-Inverse-Wishart model, for which we show that this one-time iterate optimization becomes feasible due to the approximate closed-form solutions for the local posterior distributions. The resulting algorithm is more attractive than the MAML in that it is not required to maintain computational graphs for the whole gradient optimization steps per episode. Our approach is also different from existing Bayesian meta learning methods in that unlike dealing with a single random variable for the whole episodes, our approach has a hierarchical structure that allows one-time episodic optimization, desirable for principled Bayesian learning with many/infinite tasks. The code is available at \url{https://github.com/minyoungkim21/niwmeta}.