REVE: Regularizing Deep Learning with Variational Entropy Bound

Studies on generalization performance of machine learning algorithms under the scope of information theory suggest that compressed representations can guarantee good generalization, inspiring many compression-based regularization methods. In this paper, we introduce REVE, a new regularization scheme. Noting that compressing the representation can be sub-optimal, our first contribution is to identify a variable that is directly responsible for the final prediction. Our method aims at compressing the class conditioned entropy of this latter variable. Second, we introduce a variational upper bound on this conditional entropy term. Finally, we propose a scheme to instantiate a tractable loss that is integrated within the training procedure of the neural network and demonstrate its efficiency on different neural networks and datasets.

A Characterization of Mean Squared Error for Estimator with Bagging

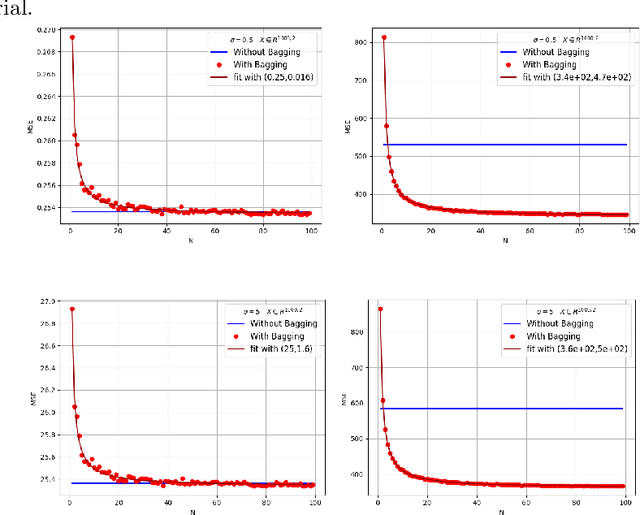
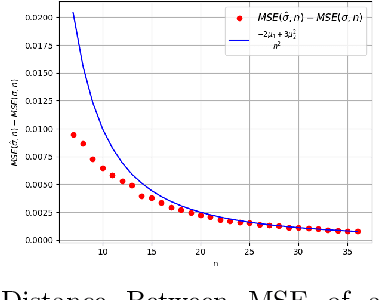
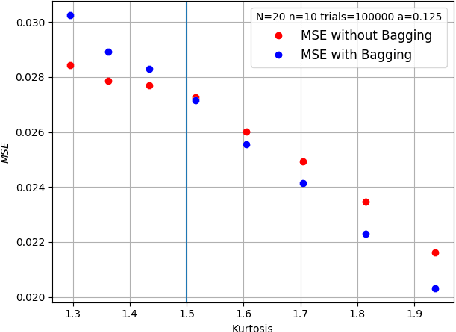
Bagging can significantly improve the generalization performance of unstable machine learning algorithms such as trees or neural networks. Though bagging is now widely used in practice and many empirical studies have explored its behavior, we still know little about the theoretical properties of bagged predictions. In this paper, we theoretically investigate how the bagging method can reduce the Mean Squared Error (MSE) when applied on a statistical estimator. First, we prove that for any estimator, increasing the number of bagged estimators $N$ in the average can only reduce the MSE. This intuitive result, observed empirically and discussed in the literature, has not yet been rigorously proved. Second, we focus on the standard estimator of variance called unbiased sample variance and we develop an exact analytical expression of the MSE for this estimator with bagging. This allows us to rigorously discuss the number of iterations $N$ and the batch size $m$ of the bagging method. From this expression, we state that only if the kurtosis of the distribution is greater than $\frac{3}{2}$, the MSE of the variance estimator can be reduced with bagging. This result is important because it demonstrates that for distribution with low kurtosis, bagging can only deteriorate the performance of a statistical prediction. Finally, we propose a novel general-purpose algorithm to estimate with high precision the variance of a sample.

SHADE: Information Based Regularization for Deep Learning

Regularization is a big issue for training deep neural networks. In this paper, we propose a new information-theory-based regularization scheme named SHADE for SHAnnon DEcay. The originality of the approach is to define a prior based on conditional entropy, which explicitly decouples the learning of invariant representations in the regularizer and the learning of correlations between inputs and labels in the data fitting term. Our second contribution is to derive a stochastic version of the regularizer compatible with deep learning, resulting in a tractable training scheme. We empirically validate the efficiency of our approach to improve classification performances compared to common regularization schemes on several standard architectures.

SHADE: Information-Based Regularization for Deep Learning

Regularization is a big issue for training deep neural networks. In this paper, we propose a new information-theory-based regularization scheme named SHADE for SHAnnon DEcay. The originality of the approach is to define a prior based on conditional entropy, which explicitly decouples the learning of invariant representations in the regularizer and the learning of correlations between inputs and labels in the data fitting term. Our second contribution is to derive a stochastic version of the regularizer compatible with deep learning, resulting in a tractable training scheme. We empirically validate the efficiency of our approach to improve classification performances compared to standard regularization schemes on several standard architectures.

GoSGD: Distributed Optimization for Deep Learning with Gossip Exchange

We address the issue of speeding up the training of convolutional neural networks by studying a distributed method adapted to stochastic gradient descent. Our parallel optimization setup uses several threads, each applying individual gradient descents on a local variable. We propose a new way of sharing information between different threads based on gossip algorithms that show good consensus convergence properties. Our method called GoSGD has the advantage to be fully asynchronous and decentralized.

Gossip training for deep learning

We address the issue of speeding up the training of convolutional networks. Here we study a distributed method adapted to stochastic gradient descent (SGD). The parallel optimization setup uses several threads, each applying individual gradient descents on a local variable. We propose a new way to share information between different threads inspired by gossip algorithms and showing good consensus convergence properties. Our method called GoSGD has the advantage to be fully asynchronous and decentralized. We compared our method to the recent EASGD in \cite{elastic} on CIFAR-10 show encouraging results.

Maxmin convolutional neural networks for image classification

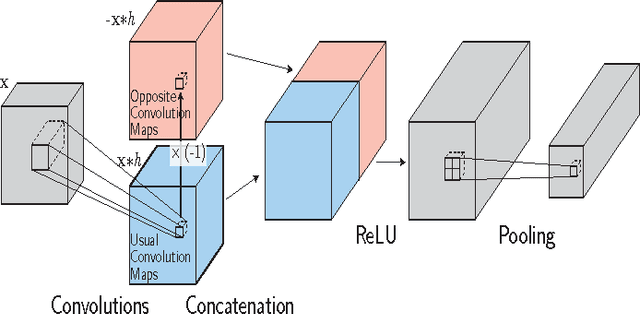
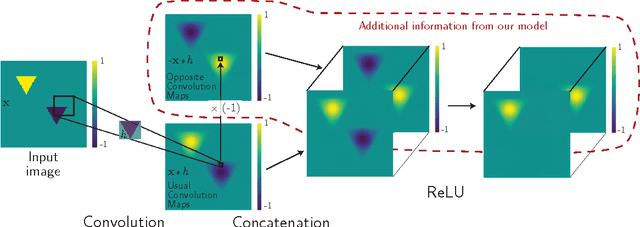
Convolutional neural networks (CNN) are widely used in computer vision, especially in image classification. However, the way in which information and invariance properties are encoded through in deep CNN architectures is still an open question. In this paper, we propose to modify the standard convo- lutional block of CNN in order to transfer more information layer after layer while keeping some invariance within the net- work. Our main idea is to exploit both positive and negative high scores obtained in the convolution maps. This behav- ior is obtained by modifying the traditional activation func- tion step before pooling. We are doubling the maps with spe- cific activations functions, called MaxMin strategy, in order to achieve our pipeline. Extensive experiments on two classical datasets, MNIST and CIFAR-10, show that our deep MaxMin convolutional net outperforms standard CNN.