Martin Mihelich
A Characterization of Mean Squared Error for Estimator with Bagging
Aug 07, 2019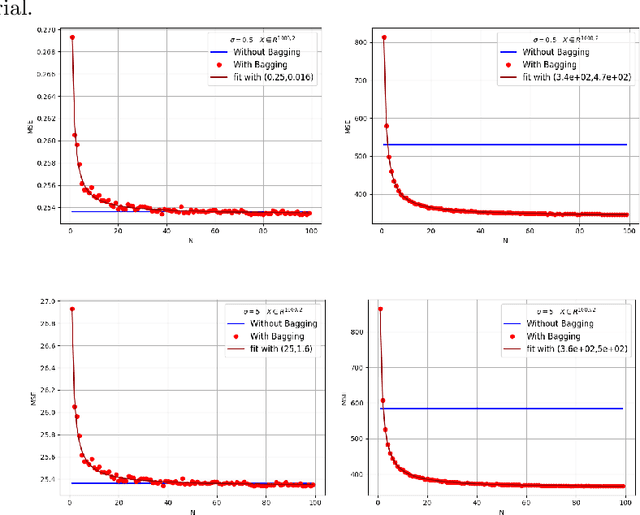
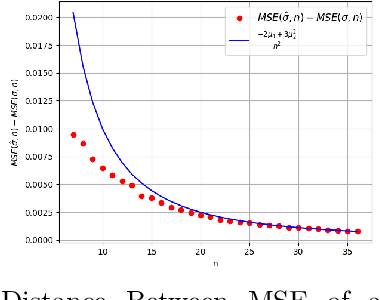
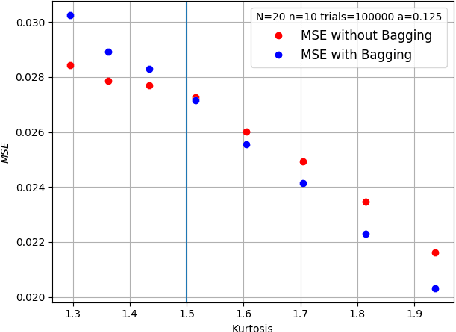
Abstract:Bagging can significantly improve the generalization performance of unstable machine learning algorithms such as trees or neural networks. Though bagging is now widely used in practice and many empirical studies have explored its behavior, we still know little about the theoretical properties of bagged predictions. In this paper, we theoretically investigate how the bagging method can reduce the Mean Squared Error (MSE) when applied on a statistical estimator. First, we prove that for any estimator, increasing the number of bagged estimators $N$ in the average can only reduce the MSE. This intuitive result, observed empirically and discussed in the literature, has not yet been rigorously proved. Second, we focus on the standard estimator of variance called unbiased sample variance and we develop an exact analytical expression of the MSE for this estimator with bagging. This allows us to rigorously discuss the number of iterations $N$ and the batch size $m$ of the bagging method. From this expression, we state that only if the kurtosis of the distribution is greater than $\frac{3}{2}$, the MSE of the variance estimator can be reduced with bagging. This result is important because it demonstrates that for distribution with low kurtosis, bagging can only deteriorate the performance of a statistical prediction. Finally, we propose a novel general-purpose algorithm to estimate with high precision the variance of a sample.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge