Sanity Check for External Clustering Validation Benchmarks using Internal Validation Measures

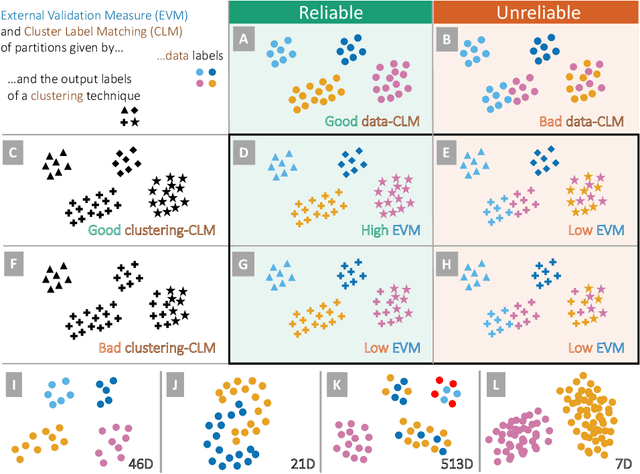
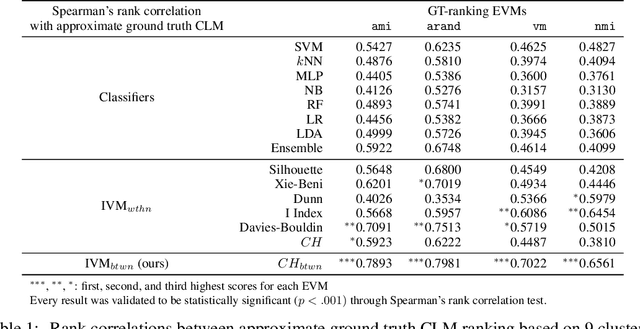
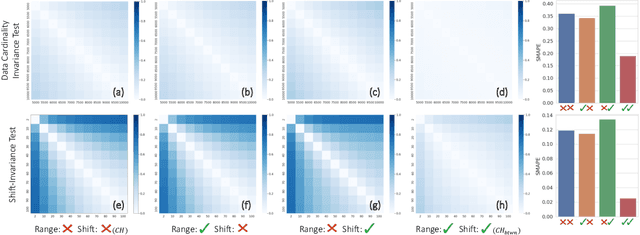
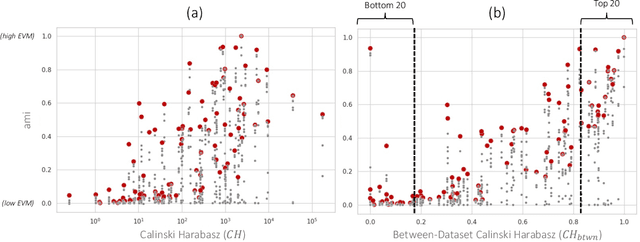
We address the lack of reliability in benchmarking clustering techniques based on labeled datasets. A standard scheme in external clustering validation is to use class labels as ground truth clusters, based on the assumption that each class forms a single, clearly separated cluster. However, as such cluster-label matching (CLM) assumption often breaks, the lack of conducting a sanity check for the CLM of benchmark datasets casts doubt on the validity of external validations. Still, evaluating the degree of CLM is challenging. For example, internal clustering validation measures can be used to quantify CLM within the same dataset to evaluate its different clusterings but are not designed to compare clusterings of different datasets. In this work, we propose a principled way to generate between-dataset internal measures that enable the comparison of CLM across datasets. We first determine four axioms for between-dataset internal measures, complementing Ackerman and Ben-David's within-dataset axioms. We then propose processes to generalize internal measures to fulfill these new axioms, and use them to extend the widely used Calinski-Harabasz index for between-dataset CLM evaluation. Through quantitative experiments, we (1) verify the validity and necessity of the generalization processes and (2) show that the proposed between-dataset Calinski-Harabasz index accurately evaluates CLM across datasets. Finally, we demonstrate the importance of evaluating CLM of benchmark datasets before conducting external validation.

ClassSPLOM -- A Scatterplot Matrix to Visualize Separation of Multiclass Multidimensional Data

In multiclass classification of multidimensional data, the user wants to build a model of the classes to predict the label of unseen data. The model is trained on the data and tested on unseen data with known labels to evaluate its quality. The results are visualized as a confusion matrix which shows how many data labels have been predicted correctly or confused with other classes. The multidimensional nature of the data prevents the direct visualization of the classes so we design ClassSPLOM to give more perceptual insights about the classification results. It uses the Scatterplot Matrix (SPLOM) metaphor to visualize a Linear Discriminant Analysis projection of the data for each pair of classes and a set of Receiving Operating Curves to evaluate their trustworthiness. We illustrate ClassSPLOM on a use case in Arabic dialects identification.

Distortion-Aware Brushing for Interactive Cluster Analysis in Multidimensional Projections

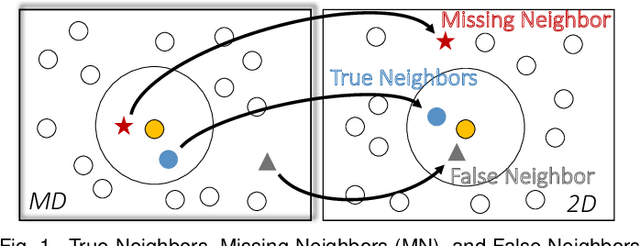
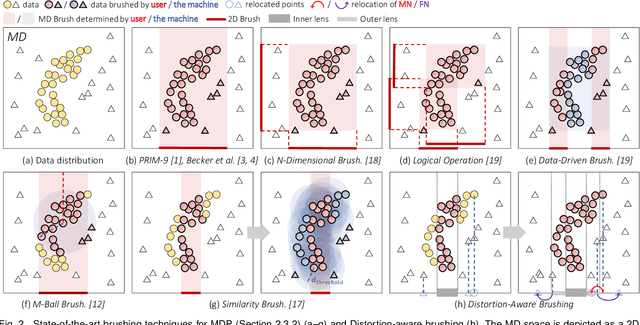
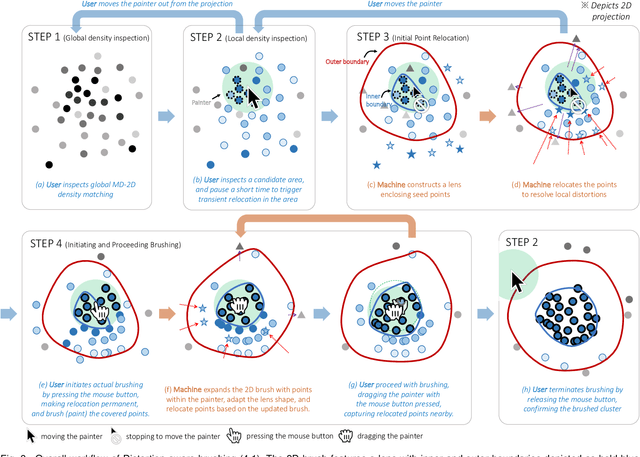
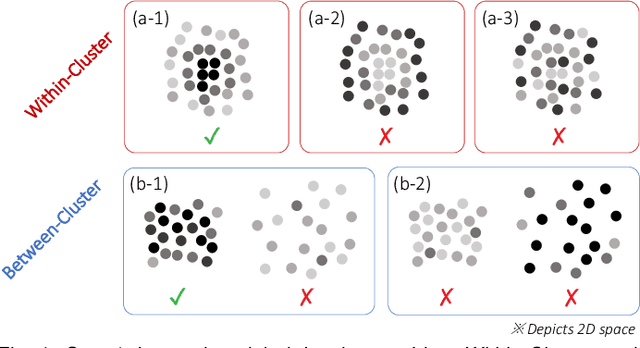
Brushing is an everyday interaction in 2D scatterplots, which allows users to select and filter data points within a continuous, enclosed region and conduct further analysis on the points. However, such conventional brushing cannot be directly applied to Multidimensional Projections (MDP), as they hardly escape from False and Missing Neighbors distortions that make the relative positions of the points unreliable. To alleviate this problem, we introduce Distortion-aware brushing, a novel brushing technique for MDP. While users perform brushing, Distortion-aware brushing resolves distortions around currently brushed points by dynamically relocating points in the projection; the points whose data are close to the brushed data in the multidimensional (MD) space go near the corresponding brushed points in the projection, and the opposites move away. Hence, users can overcome distortions and readily extract out clustered data in the MD space using the technique. We demonstrate the effectiveness and applicability of Distortion-aware brushing through usage scenarios with two datasets. Finally, by conducting user studies with 30 participants, we verified that Distortion-aware brushing significantly outperforms previous brushing techniques in precisely separating clusters in the MD space, and works robustly regardless of the types or the amount of distortions in MDP.

ClustRank: a Visual Quality Measure Trained on Perceptual Data for Sorting Scatterplots by Cluster Patterns

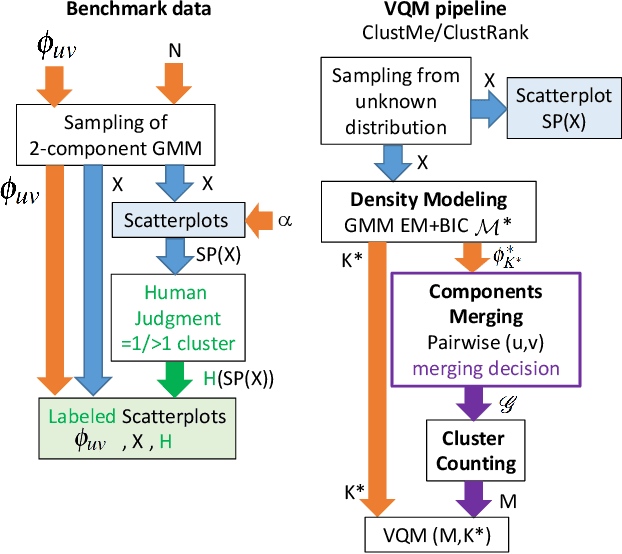
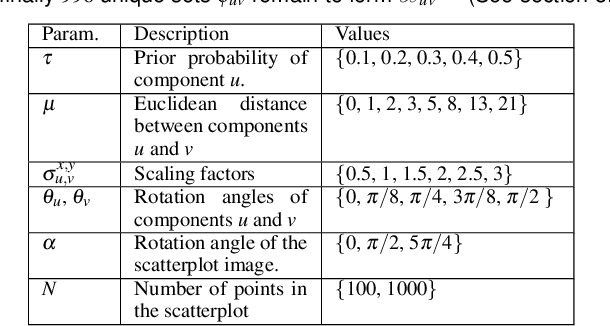
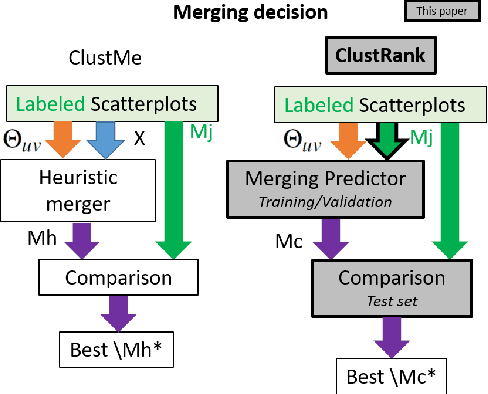
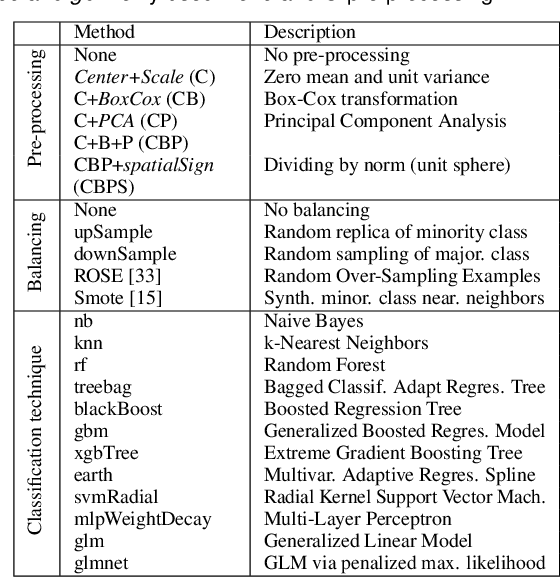
Visual quality measures (VQMs) are designed to support analysts by automatically detecting and quantifying patterns in visualizations. We propose a new data-driven technique called ClustRank that allows to rank scatterplots according to visible grouping patterns. Our model first encodes scatterplots in the parametric space of a Gaussian Mixture Model, and then uses a classifier trained on human judgment data to estimate the perceptual complexity of grouping patterns. The numbers of initial mixture components and final combined groups determine the rank of the scatterplot. ClustRank improves on existing VQM techniques by mimicking human judgments on two-Gaussian cluster patterns and gives more accuracy when ranking general cluster patterns in scatterplots. We demonstrate its benefit by analyzing kinship data for genome-wide association studies, a domain in which experts rely on the visual analysis of large sets of scatterplots. We make the three benchmark datasets and the ClustRank VQM available for practical use and further improvements.

Concerning the differentiability of the energy function in vector quantization algorithms

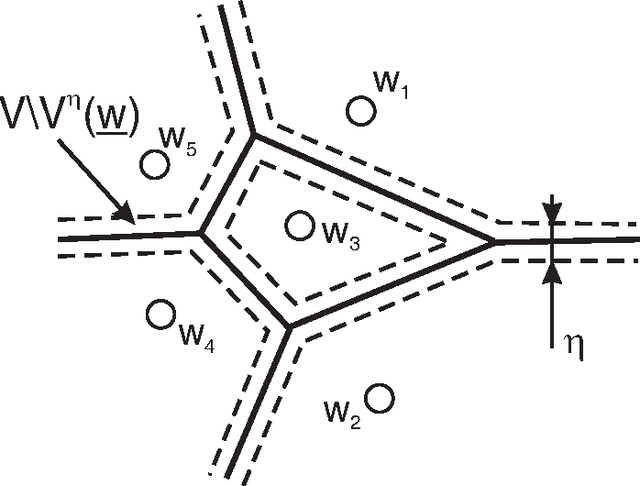
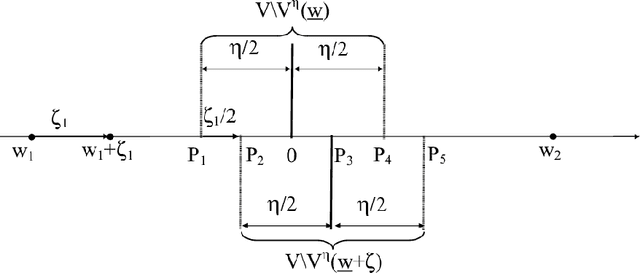
The adaptation rule for Vector Quantization algorithms, and consequently the convergence of the generated sequence, depends on the existence and properties of a function called the energy function, defined on a topological manifold. Our aim is to investigate the conditions of existence of such a function for a class of algorithms examplified by the initial ''K-means'' and Kohonen algorithms. The results presented here supplement previous studies and show that the energy function is not always a potential but at least the uniform limit of a series of potential functions which we call a pseudo-potential. Our work also shows that a large number of existing vector quantization algorithms developped by the Artificial Neural Networks community fall into this category. The framework we define opens the way to study the convergence of all the corresponding adaptation rules at once, and a theorem gives promising insights in that direction. We also demonstrate that the ''K-means'' energy function is a pseudo-potential but not a potential in general. Consequently, the energy function associated to the ''Neural-Gas'' is not a potential in general.