Mengyang Yu
Auto-Encoding Twin-Bottleneck Hashing
Mar 16, 2020



Abstract:Conventional unsupervised hashing methods usually take advantage of similarity graphs, which are either pre-computed in the high-dimensional space or obtained from random anchor points. On the one hand, existing methods uncouple the procedures of hash function learning and graph construction. On the other hand, graphs empirically built upon original data could introduce biased prior knowledge of data relevance, leading to sub-optimal retrieval performance. In this paper, we tackle the above problems by proposing an efficient and adaptive code-driven graph, which is updated by decoding in the context of an auto-encoder. Specifically, we introduce into our framework twin bottlenecks (i.e., latent variables) that exchange crucial information collaboratively. One bottleneck (i.e., binary codes) conveys the high-level intrinsic data structure captured by the code-driven graph to the other (i.e., continuous variables for low-level detail information), which in turn propagates the updated network feedback for the encoder to learn more discriminative binary codes. The auto-encoding learning objective literally rewards the code-driven graph to learn an optimal encoder. Moreover, the proposed model can be simply optimized by gradient descent without violating the binary constraints. Experiments on benchmarked datasets clearly show the superiority of our framework over the state-of-the-art hashing methods. Our source code can be found at https://github.com/ymcidence/TBH.
Fast Large-Scale Discrete Optimization Based on Principal Coordinate Descent
Sep 16, 2019



Abstract:Binary optimization, a representative subclass of discrete optimization, plays an important role in mathematical optimization and has various applications in computer vision and machine learning. Usually, binary optimization problems are NP-hard and difficult to solve due to the binary constraints, especially when the number of variables is very large. Existing methods often suffer from high computational costs or large accumulated quantization errors, or are only designed for specific tasks. In this paper, we propose a fast algorithm to find effective approximate solutions for general binary optimization problems. The proposed algorithm iteratively solves minimization problems related to the linear surrogates of loss functions, which leads to the updating of some binary variables most impacting the value of loss functions in each step. Our method supports a wide class of empirical objective functions with/without restrictions on the numbers of $1$s and $-1$s in the binary variables. Furthermore, the theoretical convergence of our algorithm is proven, and the explicit convergence rates are derived, for objective functions with Lipschitz continuous gradients, which are commonly adopted in practice. Extensive experiments on several binary optimization tasks and large-scale datasets demonstrate the superiority of the proposed algorithm over several state-of-the-art methods in terms of both effectiveness and efficiency.
STAR: A Structure and Texture Aware Retinex Model
Jun 30, 2019



Abstract:Retinex theory is developed mainly to decompose an image into the illumination and reflectance components by analyzing local image derivatives. In this theory, larger derivatives are attributed to the changes in piece-wise constant reflectance, while smaller derivatives are emerged in the smooth illumination. In this paper, we propose to utilize the exponentiated derivatives (with an exponent $\gamma$) of an observed image to generate a structure map when being amplified with $\gamma>1$ and a texture map when being shrank with $\gamma<1$. To this end, we design exponential filters for the local derivatives, and present their capability on extracting accurate structure and texture maps, influenced by the choices of exponents $\gamma$ on the local derivatives. The extracted structure and texture maps are employed to regularize the illumination and reflectance components in Retinex decomposition. A novel Structure and Texture Aware Retinex (STAR) model is further proposed for illumination and reflectance decomposition of a single image. We solve the STAR model in an alternating minimization manner. Each sub-problem is transformed into a vectorized least squares regression with closed-form solution. Comprehensive experiments demonstrate that, the proposed STAR model produce better quantitative and qualitative performance than previous competing methods, on illumination and reflectance estimation, low-light image enhancement, and color correction. The code will be publicly released.
Projection Bank: From High-dimensional Data to Medium-length Binary Codes
Sep 16, 2015



Abstract:Recently, very high-dimensional feature representations, e.g., Fisher Vector, have achieved excellent performance for visual recognition and retrieval. However, these lengthy representations always cause extremely heavy computational and storage costs and even become unfeasible in some large-scale applications. A few existing techniques can transfer very high-dimensional data into binary codes, but they still require the reduced code length to be relatively long to maintain acceptable accuracies. To target a better balance between computational efficiency and accuracies, in this paper, we propose a novel embedding method called Binary Projection Bank (BPB), which can effectively reduce the very high-dimensional representations to medium-dimensional binary codes without sacrificing accuracies. Instead of using conventional single linear or bilinear projections, the proposed method learns a bank of small projections via the max-margin constraint to optimally preserve the intrinsic data similarity. We have systematically evaluated the proposed method on three datasets: Flickr 1M, ILSVR2010 and UCF101, showing competitive retrieval and recognition accuracies compared with state-of-the-art approaches, but with a significantly smaller memory footprint and lower coding complexity.
Kernelized Multiview Projection
Aug 04, 2015
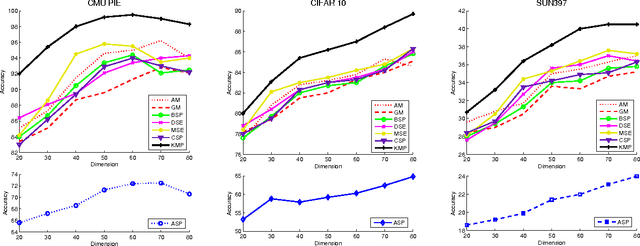
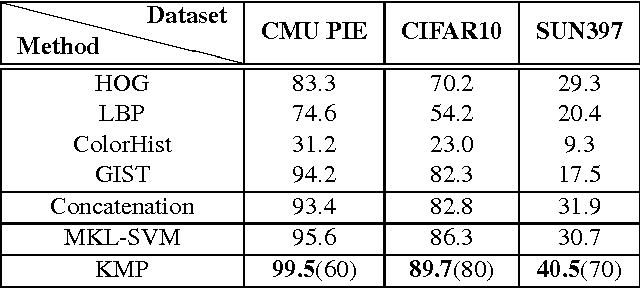
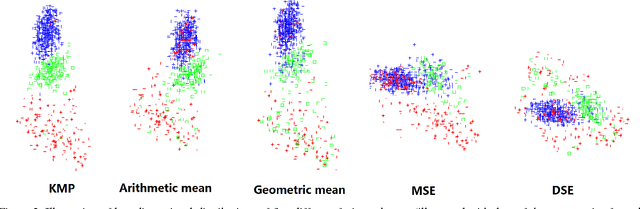
Abstract:Conventional vision algorithms adopt a single type of feature or a simple concatenation of multiple features, which is always represented in a high-dimensional space. In this paper, we propose a novel unsupervised spectral embedding algorithm called Kernelized Multiview Projection (KMP) to better fuse and embed different feature representations. Computing the kernel matrices from different features/views, KMP can encode them with the corresponding weights to achieve a low-dimensional and semantically meaningful subspace where the distribution of each view is sufficiently smooth and discriminative. More crucially, KMP is linear for the reproducing kernel Hilbert space (RKHS) and solves the out-of-sample problem, which allows it to be competent for various practical applications. Extensive experiments on three popular image datasets demonstrate the effectiveness of our multiview embedding algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge