Geometrically Guided Integrated Gradients

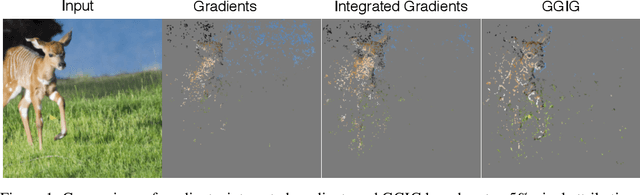
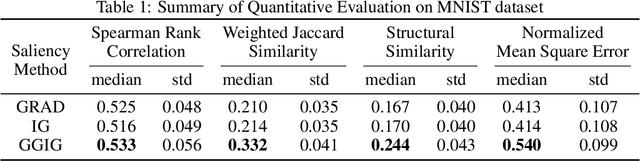
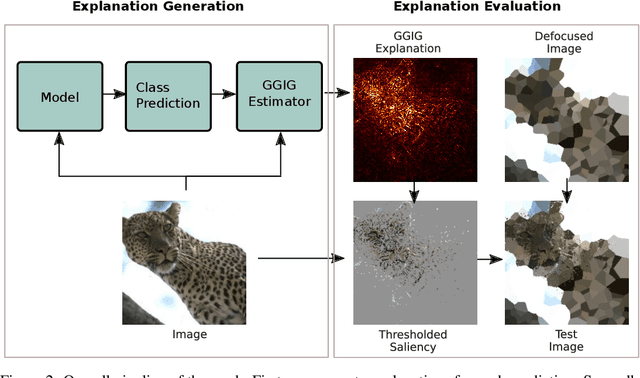
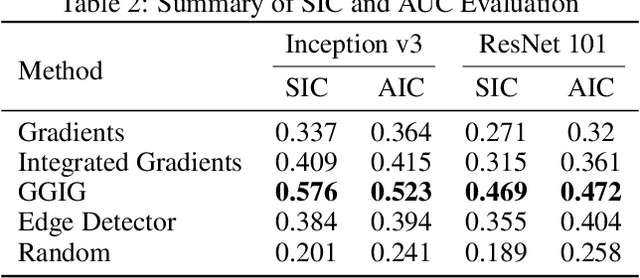
Interpretability methods for deep neural networks mainly focus on the sensitivity of the class score with respect to the original or perturbed input, usually measured using actual or modified gradients. Some methods also use a model-agnostic approach to understanding the rationale behind every prediction. In this paper, we argue and demonstrate that local geometry of the model parameter space relative to the input can also be beneficial for improved post-hoc explanations. To achieve this goal, we introduce an interpretability method called "geometrically-guided integrated gradients" that builds on top of the gradient calculation along a linear path as traditionally used in integrated gradient methods. However, instead of integrating gradient information, our method explores the model's dynamic behavior from multiple scaled versions of the input and captures the best possible attribution for each input. We demonstrate through extensive experiments that the proposed approach outperforms vanilla and integrated gradients in subjective and quantitative assessment. We also propose a "model perturbation" sanity check to complement the traditionally used "model randomization" test.

Whole MILC: generalizing learned dynamics across tasks, datasets, and populations

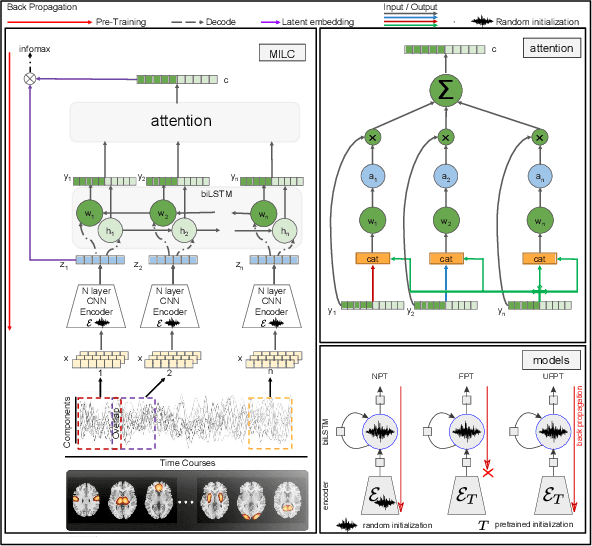
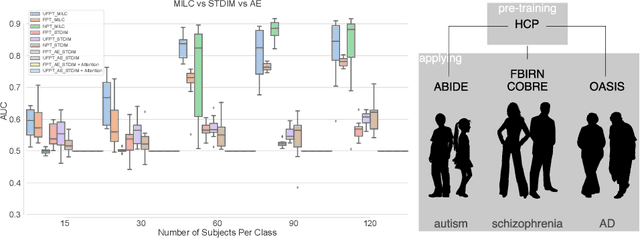
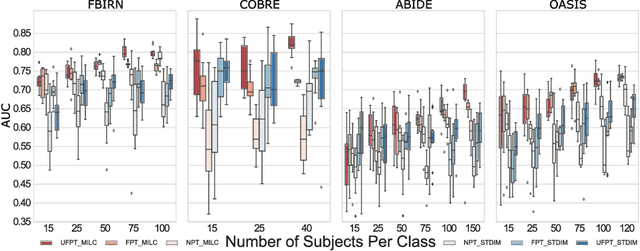
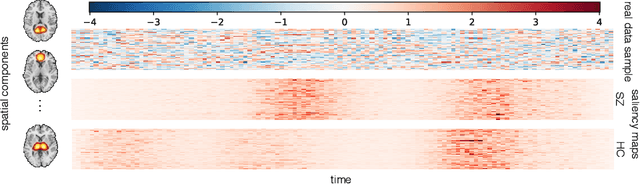
Behavioral changes are the earliest signs of a mental disorder, but arguably, the dynamics of brain function gets affected even earlier. Subsequently, spatio-temporal structure of disorder-specific dynamics is crucial for early diagnosis and understanding the disorder mechanism. A common way of learning discriminatory features relies on training a classifier and evaluating feature importance. Classical classifiers, based on handcrafted features are quite powerful, but suffer the curse of dimensionality when applied to large input dimensions of spatio-temporal data. Deep learning algorithms could handle the problem and a model introspection could highlight discriminatory spatio-temporal regions but need way more samples to train. In this paper we present a novel self supervised training schema which reinforces whole sequence mutual information local to context (whole MILC). We pre-train the whole MILC model on unlabeled and unrelated healthy control data. We test our model on three different disorders (i) Schizophrenia (ii) Autism and (iii) Alzheimers and four different studies. Our algorithm outperforms existing self-supervised pre-training methods and provides competitive classification results to classical machine learning algorithms. Importantly, whole MILC enables attribution of subject diagnosis to specific spatio-temporal regions in the fMRI signal.

Transfer Learning of fMRI Dynamics

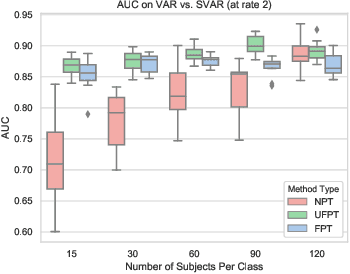
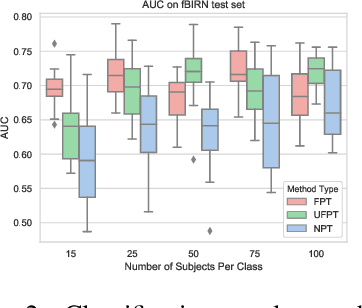
As a mental disorder progresses, it may affect brain structure, but brain function expressed in brain dynamics is affected much earlier. Capturing the moment when brain dynamics express the disorder is crucial for early diagnosis. The traditional approach to this problem via training classifiers either proceeds from handcrafted features or requires large datasets to combat the $m>>n$ problem when a high dimensional fMRI volume only has a single label that carries learning signal. Large datasets may not be available for a study of each disorder, or rare disorder types or sub-populations may not warrant for them. In this paper, we demonstrate a self-supervised pre-training method that enables us to pre-train directly on fMRI dynamics of healthy control subjects and transfer the learning to much smaller datasets of schizophrenia. Not only we enable classification of disorder directly based on fMRI dynamics in small data but also significantly speed up the learning when possible. This is encouraging evidence of informative transfer learning across datasets and diagnostic categories.

GLIMPS: A Greedy Mixed Integer Approach for Super Robust Matched Subspace Detection

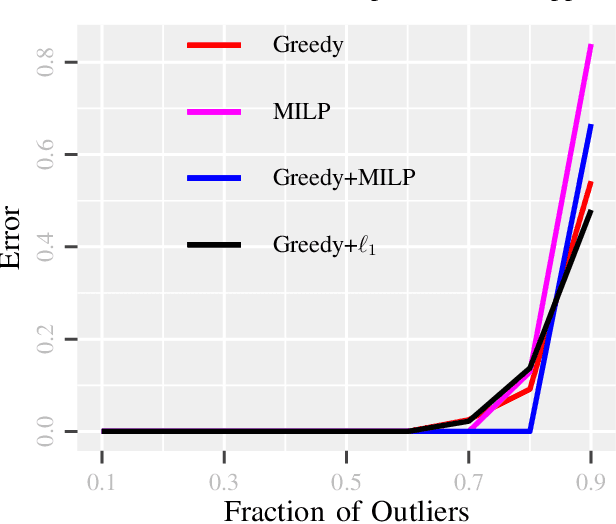
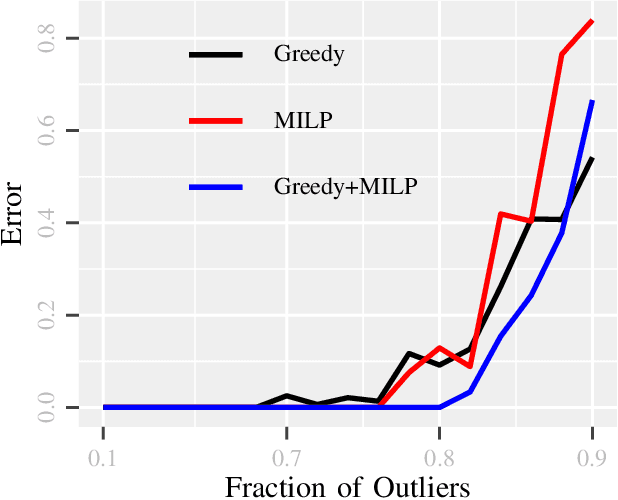
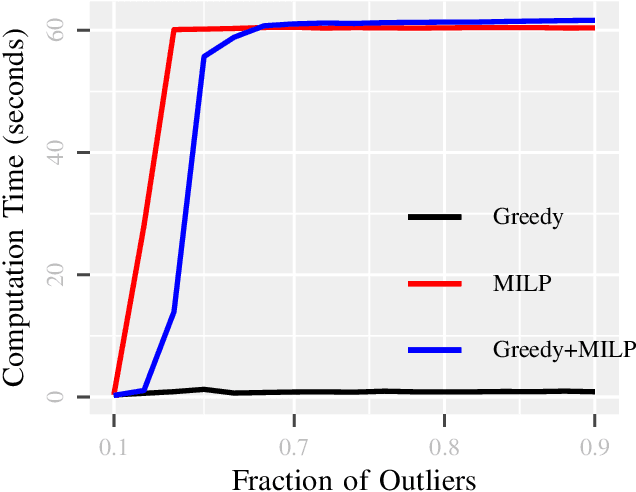
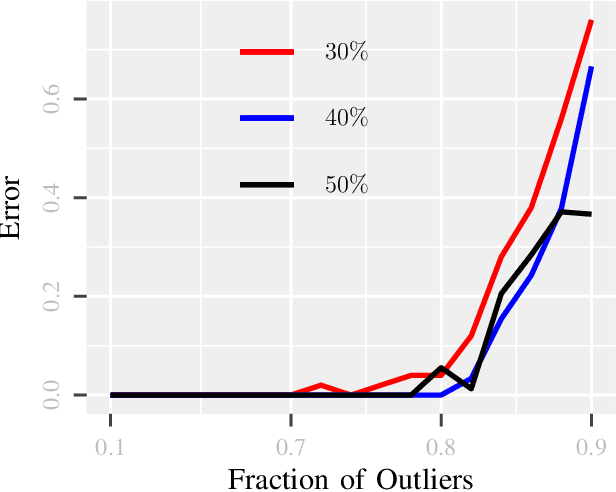
Due to diverse nature of data acquisition and modern applications, many contemporary problems involve high dimensional datum $\x \in \R^\d$ whose entries often lie in a union of subspaces and the goal is to find out which entries of $\x$ match with a particular subspace $\sU$, classically called \emph {matched subspace detection}. Consequently, entries that match with one subspace are considered as inliers w.r.t the subspace while all other entries are considered as outliers. Proportion of outliers relative to each subspace varies based on the degree of coordinates from subspaces. This problem is a combinatorial NP-hard in nature and has been immensely studied in recent years. Existing approaches can solve the problem when outliers are sparse. However, if outliers are abundant or in other words if $\x$ contains coordinates from a fair amount of subspaces, this problem can't be solved with acceptable accuracy or within a reasonable amount of time. This paper proposes a two-stage approach called \emph{Greedy Linear Integer Mixed Programmed Selector} (GLIMPS) for this abundant-outliers setting, which combines a greedy algorithm and mixed integer formulation and can tolerate over 80\% outliers, outperforming the state-of-the-art.