Geometrically Guided Integrated Gradients
Paper and Code
Jun 16, 2022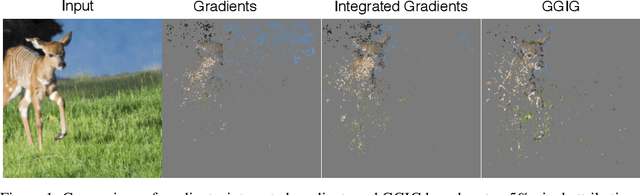
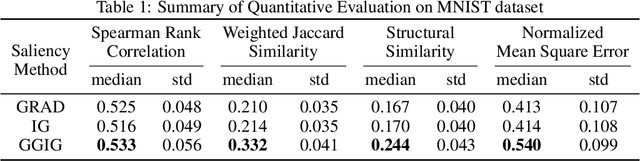
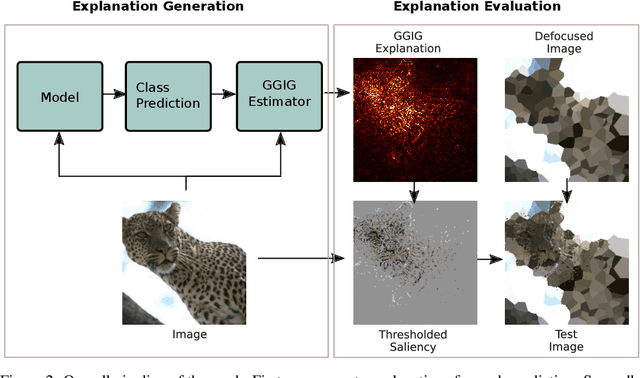
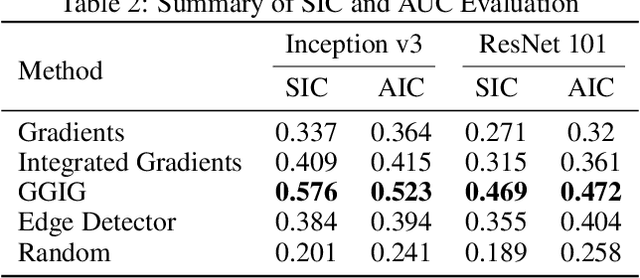
Interpretability methods for deep neural networks mainly focus on the sensitivity of the class score with respect to the original or perturbed input, usually measured using actual or modified gradients. Some methods also use a model-agnostic approach to understanding the rationale behind every prediction. In this paper, we argue and demonstrate that local geometry of the model parameter space relative to the input can also be beneficial for improved post-hoc explanations. To achieve this goal, we introduce an interpretability method called "geometrically-guided integrated gradients" that builds on top of the gradient calculation along a linear path as traditionally used in integrated gradient methods. However, instead of integrating gradient information, our method explores the model's dynamic behavior from multiple scaled versions of the input and captures the best possible attribution for each input. We demonstrate through extensive experiments that the proposed approach outperforms vanilla and integrated gradients in subjective and quantitative assessment. We also propose a "model perturbation" sanity check to complement the traditionally used "model randomization" test.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge