Classification of animal sounds in a hyperdiverse rainforest using Convolutional Neural Networks

To protect tropical forest biodiversity, we need to be able to detect it reliably, cheaply, and at scale. Automated species detection from passively recorded soundscapes via machine-learning approaches is a promising technique towards this goal, but it is constrained by the necessity of large training data sets. Using soundscapes from a tropical forest in Borneo and a Convolutional Neural Network model (CNN) created with transfer learning, we investigate i) the minimum viable training data set size for accurate prediction of call types ('sonotypes'), and ii) the extent to which data augmentation can overcome the issue of small training data sets. We found that even relatively high sample sizes (> 80 per call type) lead to mediocre accuracy, which however improves significantly with data augmentation, including at extremely small sample sizes, regardless of taxonomic group or call characteristics. Our results suggest that transfer learning and data augmentation can make the use of CNNs to classify species' vocalizations feasible even for small soundscape-based projects with many rare species. Our open-source method has the potential to enable conservation initiatives become more evidence-based by using soundscape data in the adaptive management of biodiversity.

GLIMPS: A Greedy Mixed Integer Approach for Super Robust Matched Subspace Detection

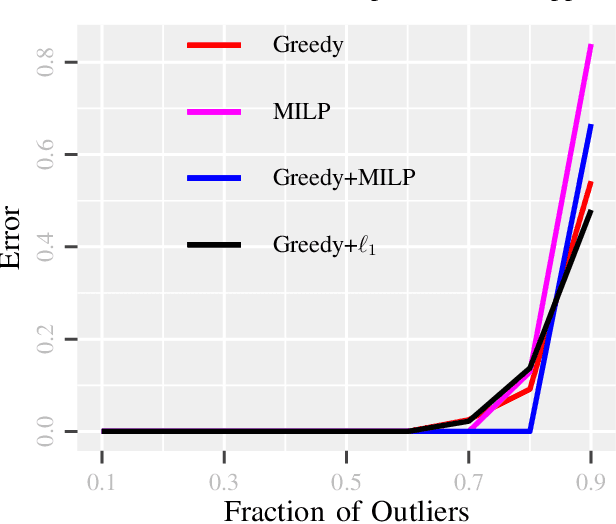
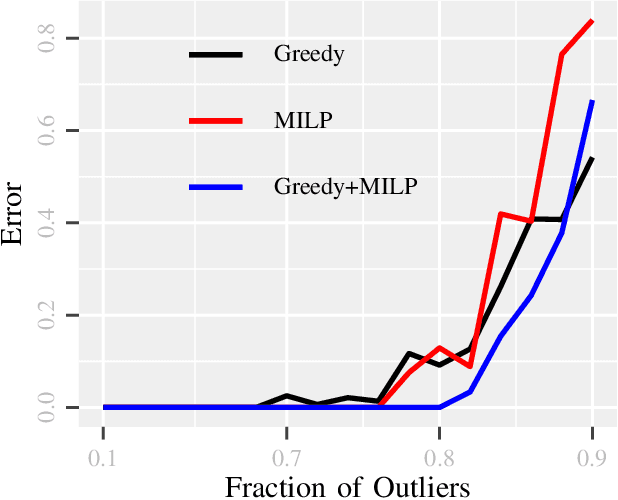
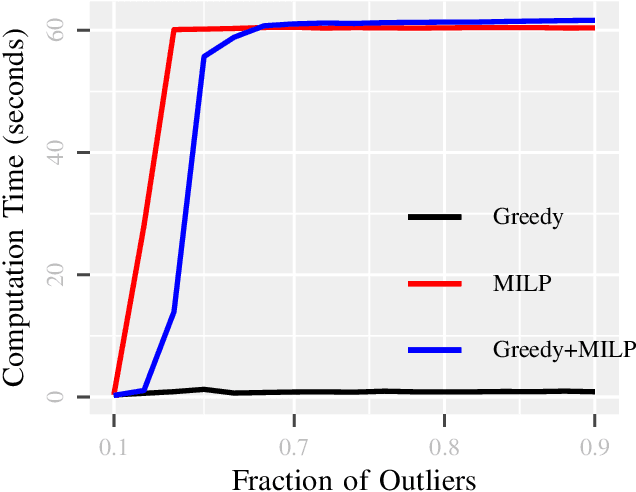
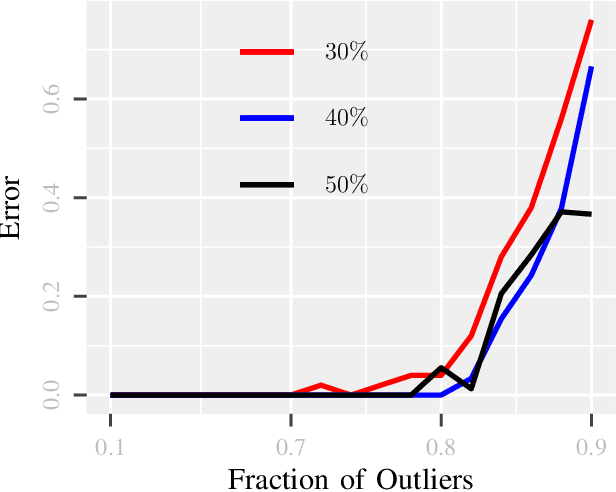
Due to diverse nature of data acquisition and modern applications, many contemporary problems involve high dimensional datum $\x \in \R^\d$ whose entries often lie in a union of subspaces and the goal is to find out which entries of $\x$ match with a particular subspace $\sU$, classically called \emph {matched subspace detection}. Consequently, entries that match with one subspace are considered as inliers w.r.t the subspace while all other entries are considered as outliers. Proportion of outliers relative to each subspace varies based on the degree of coordinates from subspaces. This problem is a combinatorial NP-hard in nature and has been immensely studied in recent years. Existing approaches can solve the problem when outliers are sparse. However, if outliers are abundant or in other words if $\x$ contains coordinates from a fair amount of subspaces, this problem can't be solved with acceptable accuracy or within a reasonable amount of time. This paper proposes a two-stage approach called \emph{Greedy Linear Integer Mixed Programmed Selector} (GLIMPS) for this abundant-outliers setting, which combines a greedy algorithm and mixed integer formulation and can tolerate over 80\% outliers, outperforming the state-of-the-art.