GLIMPS: A Greedy Mixed Integer Approach for Super Robust Matched Subspace Detection
Paper and Code
Oct 29, 2019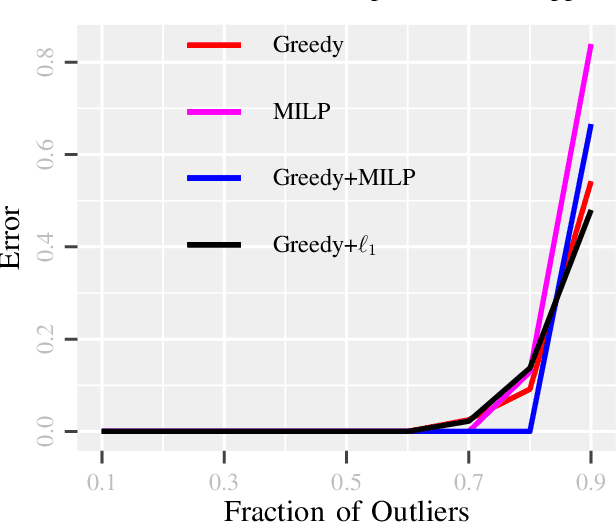
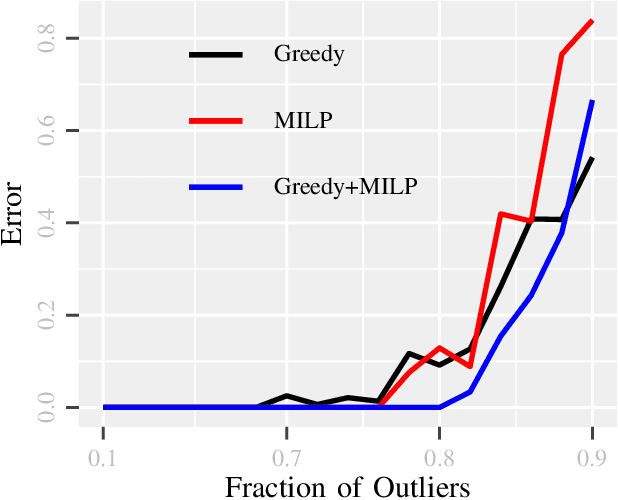
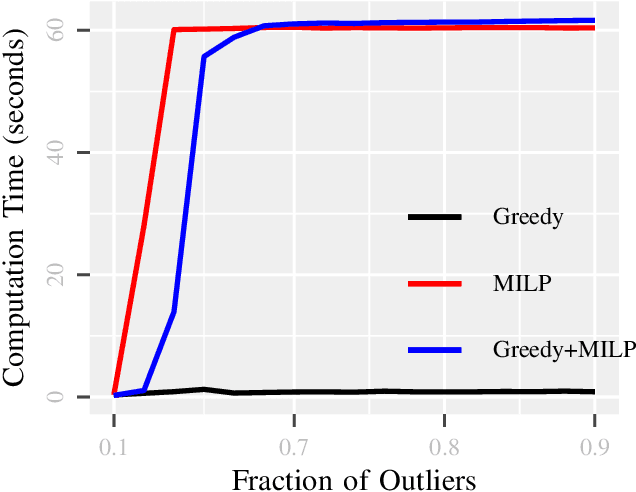
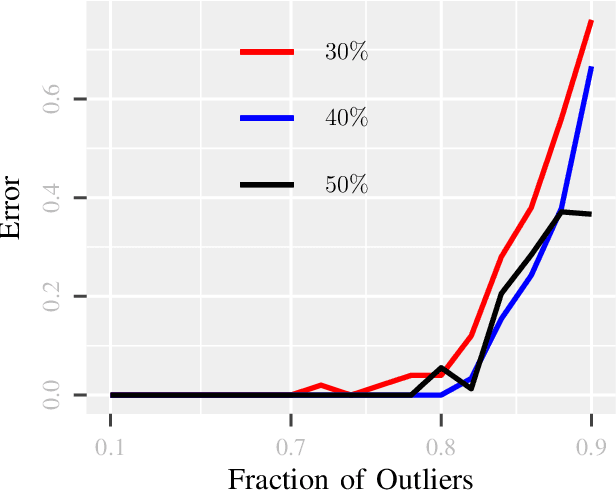
Due to diverse nature of data acquisition and modern applications, many contemporary problems involve high dimensional datum $\x \in \R^\d$ whose entries often lie in a union of subspaces and the goal is to find out which entries of $\x$ match with a particular subspace $\sU$, classically called \emph {matched subspace detection}. Consequently, entries that match with one subspace are considered as inliers w.r.t the subspace while all other entries are considered as outliers. Proportion of outliers relative to each subspace varies based on the degree of coordinates from subspaces. This problem is a combinatorial NP-hard in nature and has been immensely studied in recent years. Existing approaches can solve the problem when outliers are sparse. However, if outliers are abundant or in other words if $\x$ contains coordinates from a fair amount of subspaces, this problem can't be solved with acceptable accuracy or within a reasonable amount of time. This paper proposes a two-stage approach called \emph{Greedy Linear Integer Mixed Programmed Selector} (GLIMPS) for this abundant-outliers setting, which combines a greedy algorithm and mixed integer formulation and can tolerate over 80\% outliers, outperforming the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge