OpenMedLM: Prompt engineering can out-perform fine-tuning in medical question-answering with open-source large language models

LLMs have become increasingly capable at accomplishing a range of specialized-tasks and can be utilized to expand equitable access to medical knowledge. Most medical LLMs have involved extensive fine-tuning, leveraging specialized medical data and significant, thus costly, amounts of computational power. Many of the top performing LLMs are proprietary and their access is limited to very few research groups. However, open-source (OS) models represent a key area of growth for medical LLMs due to significant improvements in performance and an inherent ability to provide the transparency and compliance required in healthcare. We present OpenMedLM, a prompting platform which delivers state-of-the-art (SOTA) performance for OS LLMs on medical benchmarks. We evaluated a range of OS foundation LLMs (7B-70B) on four medical benchmarks (MedQA, MedMCQA, PubMedQA, MMLU medical-subset). We employed a series of prompting strategies, including zero-shot, few-shot, chain-of-thought (random selection and kNN selection), and ensemble/self-consistency voting. We found that OpenMedLM delivers OS SOTA results on three common medical LLM benchmarks, surpassing the previous best performing OS models that leveraged computationally costly extensive fine-tuning. The model delivers a 72.6% accuracy on the MedQA benchmark, outperforming the previous SOTA by 2.4%, and achieves 81.7% accuracy on the MMLU medical-subset, establishing itself as the first OS LLM to surpass 80% accuracy on this benchmark. Our results highlight medical-specific emergent properties in OS LLMs which have not yet been documented to date elsewhere, and showcase the benefits of further leveraging prompt engineering to improve the performance of accessible LLMs for medical applications.

Problems with automating translation of movie/TV show subtitles

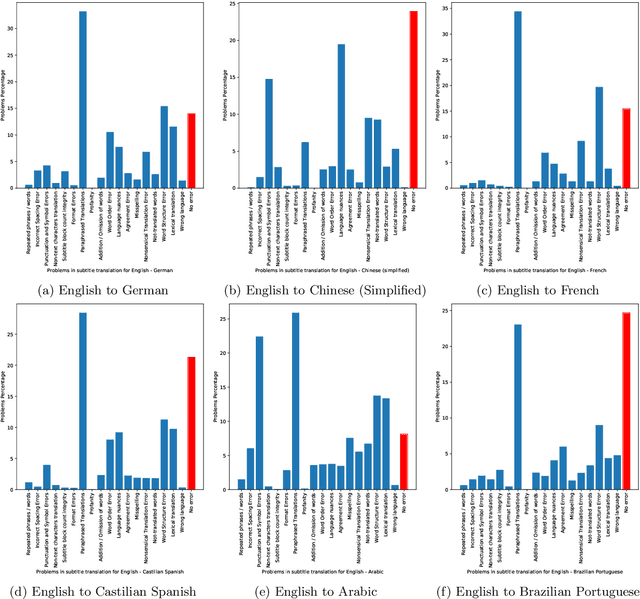
We present 27 problems encountered in automating the translation of movie/TV show subtitles. We categorize each problem in one of the three categories viz. problems directly related to textual translation, problems related to subtitle creation guidelines, and problems due to adaptability of machine translation (MT) engines. We also present the findings of a translation quality evaluation experiment where we share the frequency of 16 key problems. We show that the systems working at the frontiers of Natural Language Processing do not perform well for subtitles and require some post-processing solutions for redressal of these problems

Smaller Models, Better Generalization

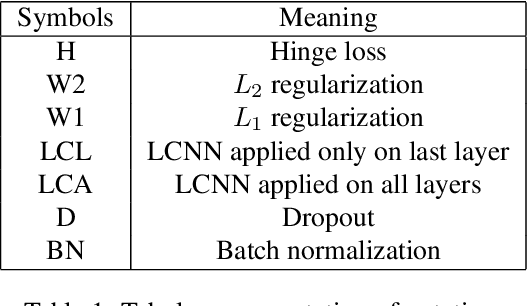
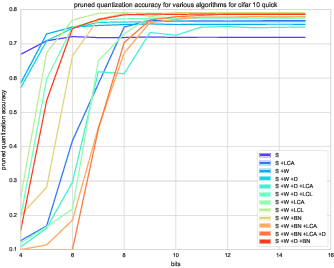
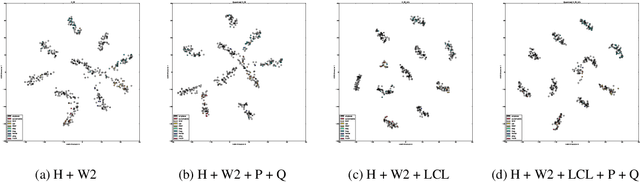
Reducing network complexity has been a major research focus in recent years with the advent of mobile technology. Convolutional Neural Networks that perform various vision tasks without memory overhaul is the need of the hour. This paper focuses on qualitative and quantitative analysis of reducing the network complexity using an upper bound on the Vapnik-Chervonenkis dimension, pruning, and quantization. We observe a general trend in improvement of accuracies as we quantize the models. We propose a novel loss function that helps in achieving considerable sparsity at comparable accuracies to that of dense models. We compare various regularizations prevalent in the literature and show the superiority of our method in achieving sparser models that generalize well.

Effect of Various Regularizers on Model Complexities of Neural Networks in Presence of Input Noise

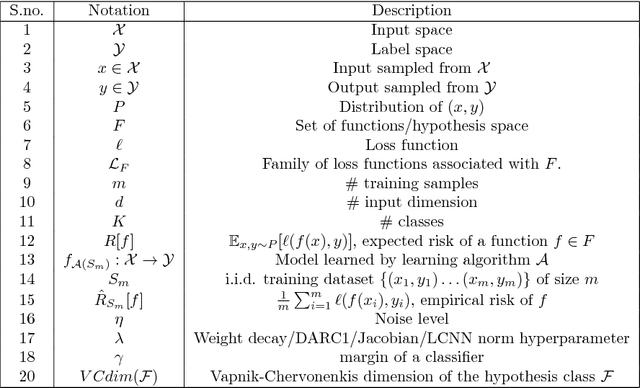
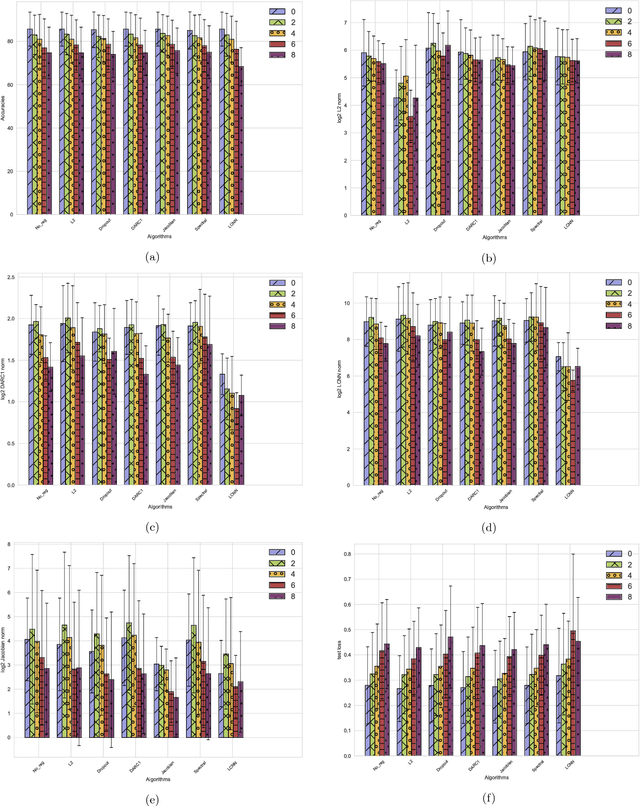
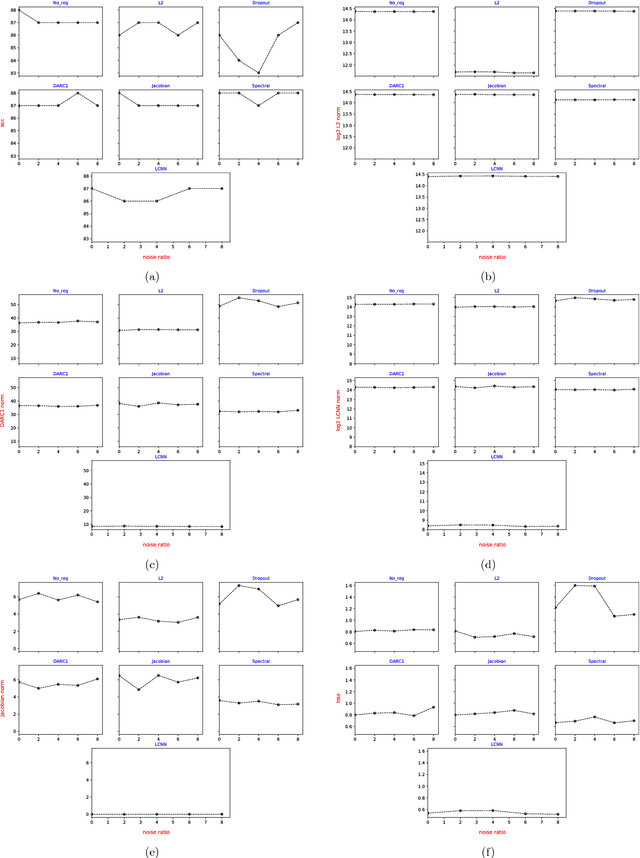
Deep neural networks are over-parameterized, which implies that the number of parameters are much larger than the number of samples used to train the network. Even in such a regime deep architectures do not overfit. This phenomenon is an active area of research and many theories have been proposed trying to understand this peculiar observation. These include the Vapnik Chervonenkis (VC) dimension bounds and Rademacher complexity bounds which show that the capacity of the network is characterized by the norm of weights rather than the number of parameters. However, the effect of input noise on these measures for shallow and deep architectures has not been studied. In this paper, we analyze the effects of various regularization schemes on the complexity of a neural network which we characterize with the loss, $L_2$ norm of the weights, Rademacher complexities (Directly Approximately Regularizing Complexity-DARC1), VC dimension based Low Complexity Neural Network (LCNN) when subject to varying degrees of Gaussian input noise. We show that $L_2$ regularization leads to a simpler hypothesis class and better generalization followed by DARC1 regularizer, both for shallow as well as deeper architectures. Jacobian regularizer works well for shallow architectures with high level of input noises. Spectral normalization attains highest test set accuracies both for shallow and deeper architectures. We also show that Dropout alone does not perform well in presence of input noise. Finally, we show that deeper architectures are robust to input noise as opposed to their shallow counterparts.

Radius-margin bounds for deep neural networks

Explaining the unreasonable effectiveness of deep learning has eluded researchers around the globe. Various authors have described multiple metrics to evaluate the capacity of deep architectures. In this paper, we allude to the radius margin bounds described for a support vector machine (SVM) with hinge loss, apply the same to the deep feed-forward architectures and derive the Vapnik-Chervonenkis (VC) bounds which are different from the earlier bounds proposed in terms of number of weights of the network. In doing so, we also relate the effectiveness of techniques like Dropout and Dropconnect in bringing down the capacity of the network. Finally, we describe the effect of maximizing the input as well as the output margin to achieve an input noise-robust deep architecture.

Scalable Twin Neural Networks for Classification of Unbalanced Data

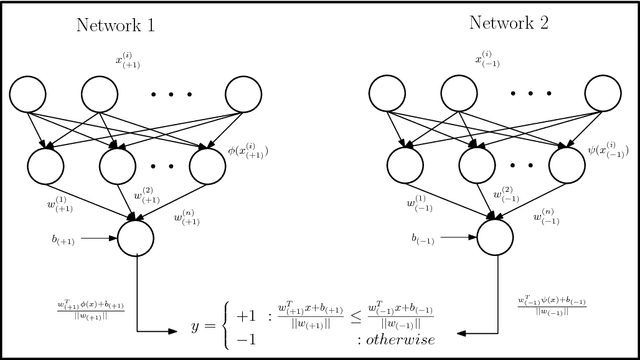
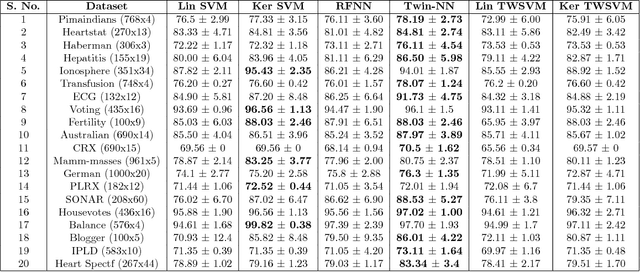
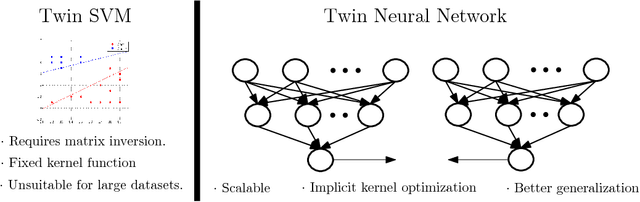
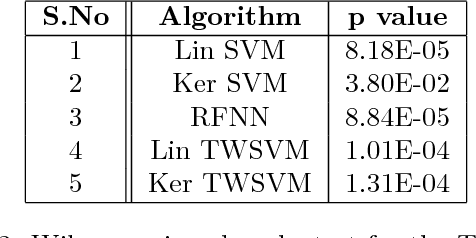
Twin Support Vector Machines (TWSVMs) have emerged an efficient alternative to Support Vector Machines (SVM) for learning from imbalanced datasets. The TWSVM learns two non-parallel classifying hyperplanes by solving a couple of smaller sized problems. However, it is unsuitable for large datasets, as it involves matrix operations. In this paper, we discuss a Twin Neural Network (Twin NN) architecture for learning from large unbalanced datasets. The Twin NN also learns an optimal feature map, allowing for better discrimination between classes. We also present an extension of this network architecture for multiclass datasets. Results presented in the paper demonstrate that the Twin NN generalizes well and scales well on large unbalanced datasets.

Learning Neural Network Classifiers with Low Model Complexity

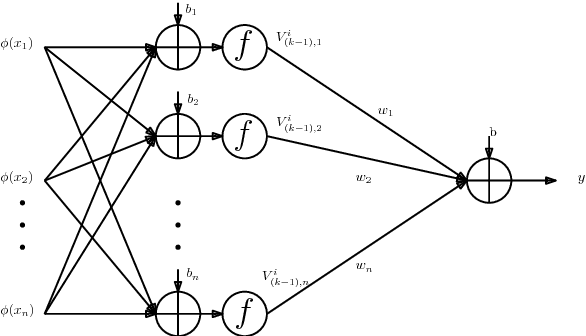
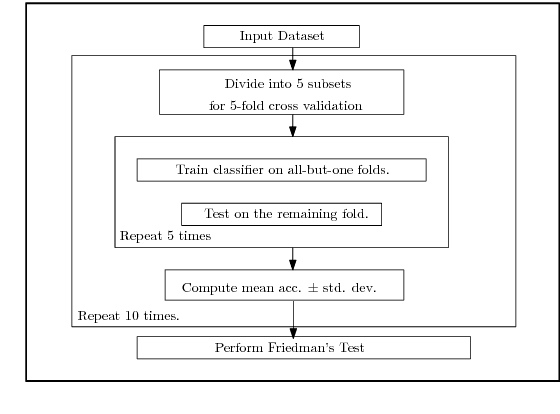
Modern neural network architectures for large-scale learning tasks have substantially higher model complexities, which makes understanding, visualizing and training these architectures difficult. Recent contributions to deep learning techniques have focused on architectural modifications to improve parameter efficiency and performance. In this paper, we derive a continuous and differentiable error functional for a neural network that minimizes its empirical error as well as a measure of the model complexity. The latter measure is obtained by deriving a differentiable upper bound on the Vapnik-Chervonenkis (VC) dimension of the classifier layer of a class of deep networks. Using standard backpropagation, we realize a training rule that tries to minimize the error on training samples, while improving generalization by keeping the model complexity low. We demonstrate the effectiveness of our formulation (the Low Complexity Neural Network - LCNN) across several deep learning algorithms, and a variety of large benchmark datasets. We show that hidden layer neurons in the resultant networks learn features that are crisp, and in the case of image datasets, quantitatively sharper. Our proposed approach yields benefits across a wide range of architectures, in comparison to and in conjunction with methods such as Dropout and Batch Normalization, and our results strongly suggest that deep learning techniques can benefit from model complexity control methods such as the LCNN learning rule.

Maximum Weight Matching via Max-Product Belief Propagation

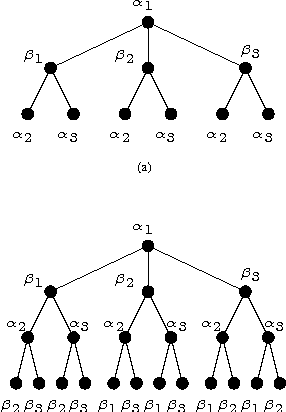
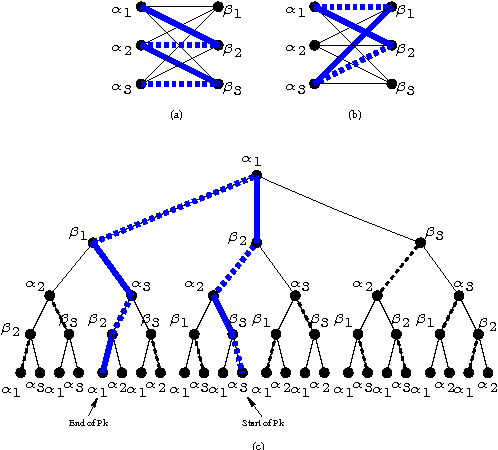
Max-product "belief propagation" is an iterative, local, message-passing algorithm for finding the maximum a posteriori (MAP) assignment of a discrete probability distribution specified by a graphical model. Despite the spectacular success of the algorithm in many application areas such as iterative decoding, computer vision and combinatorial optimization which involve graphs with many cycles, theoretical results about both correctness and convergence of the algorithm are known in few cases (Weiss-Freeman Wainwright, Yeddidia-Weiss-Freeman, Richardson-Urbanke}. In this paper we consider the problem of finding the Maximum Weight Matching (MWM) in a weighted complete bipartite graph. We define a probability distribution on the bipartite graph whose MAP assignment corresponds to the MWM. We use the max-product algorithm for finding the MAP of this distribution or equivalently, the MWM on the bipartite graph. Even though the underlying bipartite graph has many short cycles, we find that surprisingly, the max-product algorithm always converges to the correct MAP assignment as long as the MAP assignment is unique. We provide a bound on the number of iterations required by the algorithm and evaluate the computational cost of the algorithm. We find that for a graph of size $n$, the computational cost of the algorithm scales as $O(n^3)$, which is the same as the computational cost of the best known algorithm. Finally, we establish the precise relation between the max-product algorithm and the celebrated {\em auction} algorithm proposed by Bertsekas. This suggests possible connections between dual algorithm and max-product algorithm for discrete optimization problems.