Sai Guruju
Smaller Models, Better Generalization
Aug 29, 2019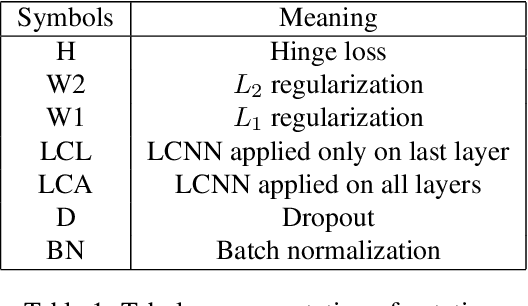
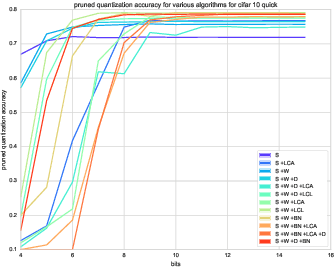

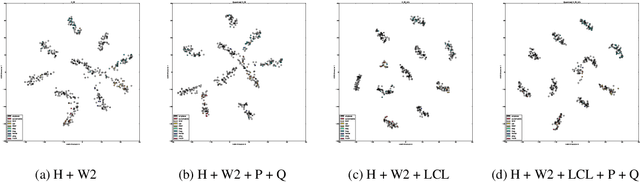
Abstract:Reducing network complexity has been a major research focus in recent years with the advent of mobile technology. Convolutional Neural Networks that perform various vision tasks without memory overhaul is the need of the hour. This paper focuses on qualitative and quantitative analysis of reducing the network complexity using an upper bound on the Vapnik-Chervonenkis dimension, pruning, and quantization. We observe a general trend in improvement of accuracies as we quantize the models. We propose a novel loss function that helps in achieving considerable sparsity at comparable accuracies to that of dense models. We compare various regularizations prevalent in the literature and show the superiority of our method in achieving sparser models that generalize well.
Learning Neural Network Classifiers with Low Model Complexity
Jan 02, 2018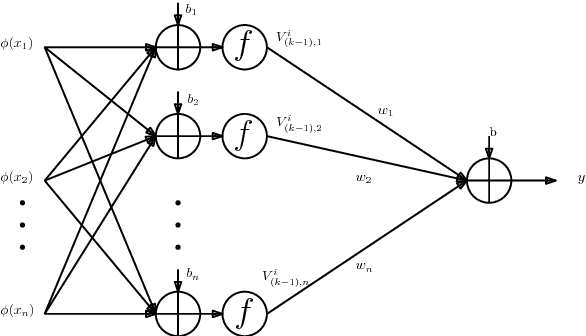

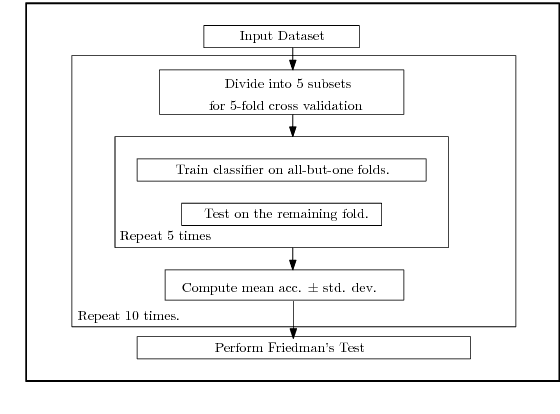

Abstract:Modern neural network architectures for large-scale learning tasks have substantially higher model complexities, which makes understanding, visualizing and training these architectures difficult. Recent contributions to deep learning techniques have focused on architectural modifications to improve parameter efficiency and performance. In this paper, we derive a continuous and differentiable error functional for a neural network that minimizes its empirical error as well as a measure of the model complexity. The latter measure is obtained by deriving a differentiable upper bound on the Vapnik-Chervonenkis (VC) dimension of the classifier layer of a class of deep networks. Using standard backpropagation, we realize a training rule that tries to minimize the error on training samples, while improving generalization by keeping the model complexity low. We demonstrate the effectiveness of our formulation (the Low Complexity Neural Network - LCNN) across several deep learning algorithms, and a variety of large benchmark datasets. We show that hidden layer neurons in the resultant networks learn features that are crisp, and in the case of image datasets, quantitatively sharper. Our proposed approach yields benefits across a wide range of architectures, in comparison to and in conjunction with methods such as Dropout and Batch Normalization, and our results strongly suggest that deep learning techniques can benefit from model complexity control methods such as the LCNN learning rule.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge