Aayush Yadav
Effect of Various Regularizers on Model Complexities of Neural Networks in Presence of Input Noise
Jan 31, 2019
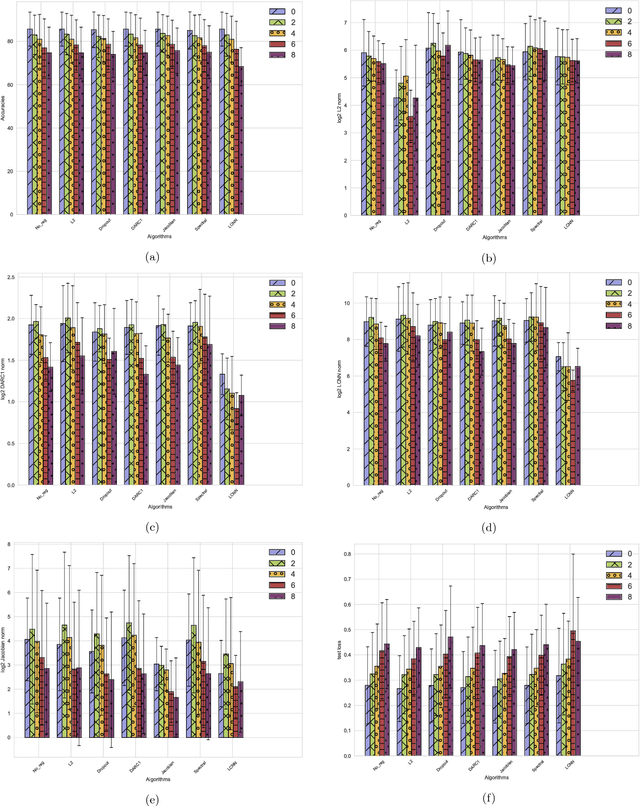

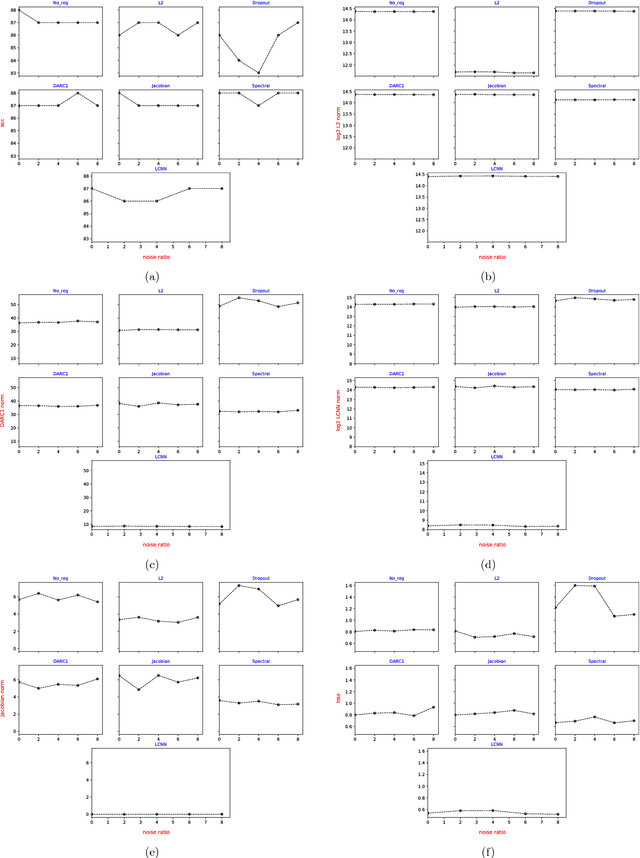
Abstract:Deep neural networks are over-parameterized, which implies that the number of parameters are much larger than the number of samples used to train the network. Even in such a regime deep architectures do not overfit. This phenomenon is an active area of research and many theories have been proposed trying to understand this peculiar observation. These include the Vapnik Chervonenkis (VC) dimension bounds and Rademacher complexity bounds which show that the capacity of the network is characterized by the norm of weights rather than the number of parameters. However, the effect of input noise on these measures for shallow and deep architectures has not been studied. In this paper, we analyze the effects of various regularization schemes on the complexity of a neural network which we characterize with the loss, $L_2$ norm of the weights, Rademacher complexities (Directly Approximately Regularizing Complexity-DARC1), VC dimension based Low Complexity Neural Network (LCNN) when subject to varying degrees of Gaussian input noise. We show that $L_2$ regularization leads to a simpler hypothesis class and better generalization followed by DARC1 regularizer, both for shallow as well as deeper architectures. Jacobian regularizer works well for shallow architectures with high level of input noises. Spectral normalization attains highest test set accuracies both for shallow and deeper architectures. We also show that Dropout alone does not perform well in presence of input noise. Finally, we show that deeper architectures are robust to input noise as opposed to their shallow counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge