Mathew Halm
A biconvex method for minimum-time motion planning through sequences of convex sets
Apr 26, 2025
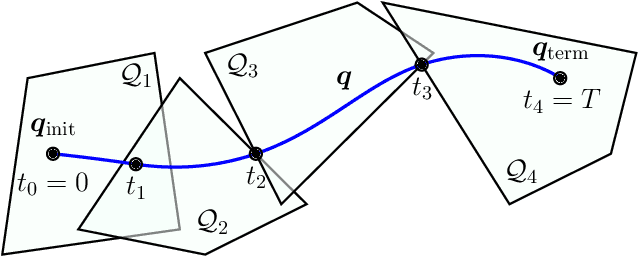
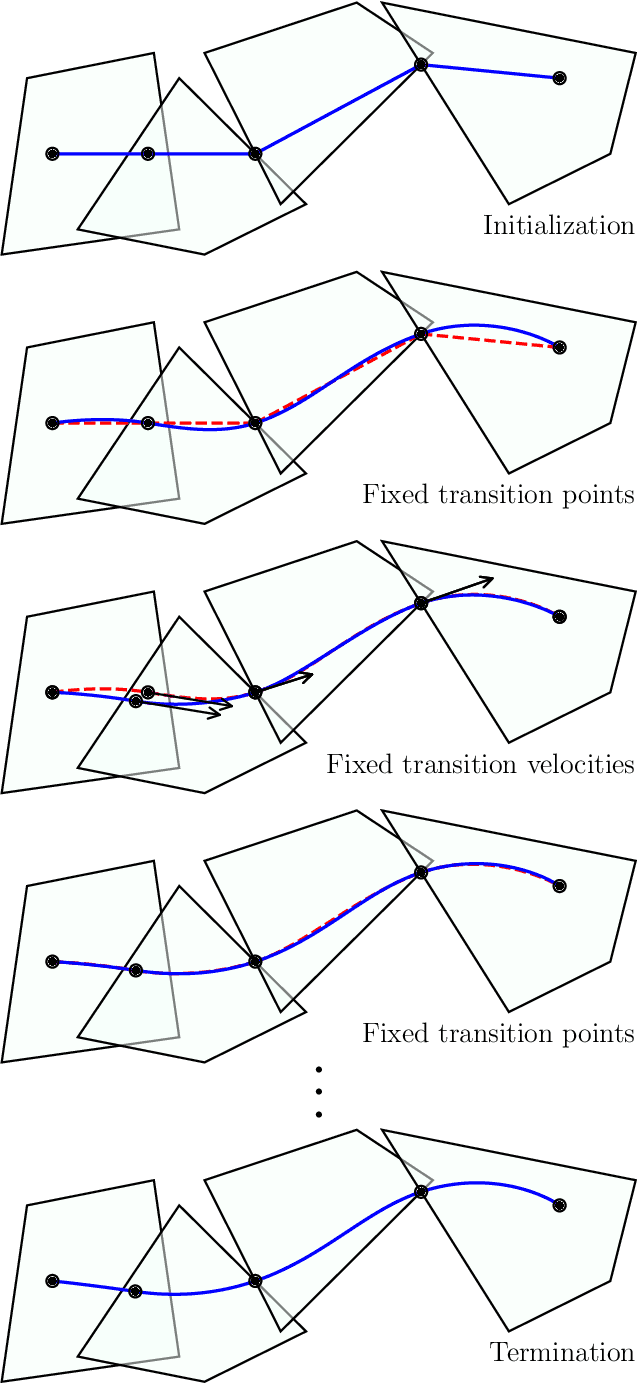
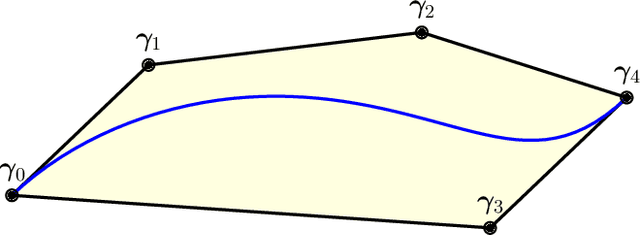
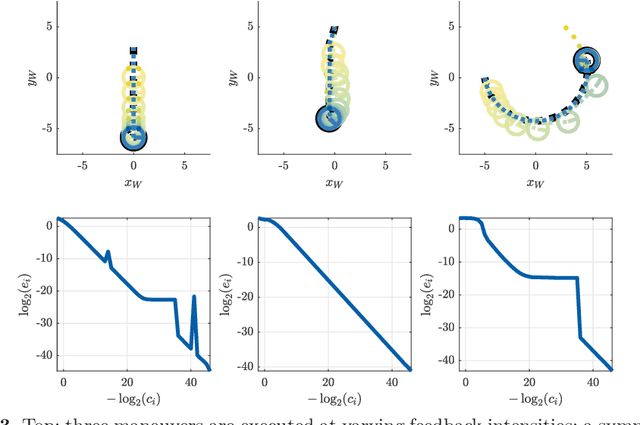
Abstract:We consider the problem of designing a smooth trajectory that traverses a sequence of convex sets in minimum time, while satisfying given velocity and acceleration constraints. This problem is naturally formulated as a nonconvex program. To solve it, we propose a biconvex method that quickly produces an initial trajectory and iteratively refines it by solving two convex subproblems in alternation. This method is guaranteed to converge, returns a feasible trajectory even if stopped early, and does not require the selection of any line-search or trust-region parameter. Exhaustive experiments show that our method finds high-quality trajectories in a fraction of the time of state-of-the-art solvers for nonconvex optimization. In addition, it achieves runtimes comparable to industry-standard waypoint-based motion planners, while consistently designing lower-duration trajectories than existing optimization-based planners.
Simultaneous Learning of Contact and Continuous Dynamics
Oct 18, 2023Abstract:Robotic manipulation can greatly benefit from the data efficiency, robustness, and predictability of model-based methods if robots can quickly generate models of novel objects they encounter. This is especially difficult when effects like complex joint friction lack clear first-principles models and are usually ignored by physics simulators. Further, numerically-stiff contact dynamics can make common model-building approaches struggle. We propose a method to simultaneously learn contact and continuous dynamics of a novel, possibly multi-link object by observing its motion through contact-rich trajectories. We formulate a system identification process with a loss that infers unmeasured contact forces, penalizing their violation of physical constraints and laws of motion given current model parameters. Our loss is unlike prediction-based losses used in differentiable simulation. Using a new dataset of real articulated object trajectories and an existing cube toss dataset, our method outperforms differentiable simulation and end-to-end alternatives with more data efficiency. See our project page for code, datasets, and media: https://sites.google.com/view/continuous-contact-nets/home
Learning Linear Complementarity Systems
Dec 25, 2021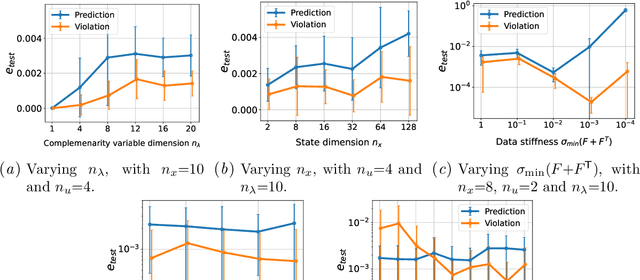
Abstract:This paper investigates the learning, or system identification, of a class of piecewise-affine dynamical systems known as linear complementarity systems (LCSs). We propose a violation-based loss which enables efficient learning of the LCS parameterization, without prior knowledge of the hybrid mode boundaries, using gradient-based methods. The proposed violation-based loss incorporates both dynamics prediction loss and a novel complementarity - violation loss. We show several properties attained by this loss formulation, including its differentiability, the efficient computation of first- and second-order derivatives, and its relationship to the traditional prediction loss, which strictly enforces complementarity. We apply this violation-based loss formulation to learn LCSs with tens of thousands of (potentially stiff) hybrid modes. The results demonstrate a state-of-the-art ability to identify piecewise-affine dynamics, outperforming methods which must differentiate through non-smooth linear complementarity problems.
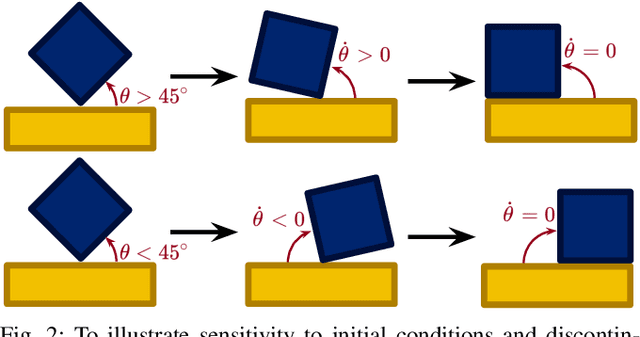
Generalization Bounded Implicit Learning of Nearly Discontinuous Functions
Dec 14, 2021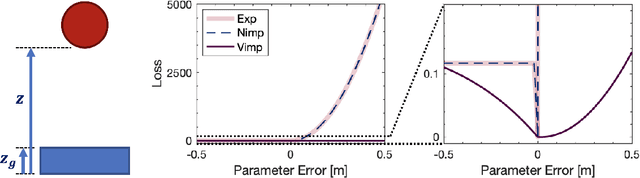
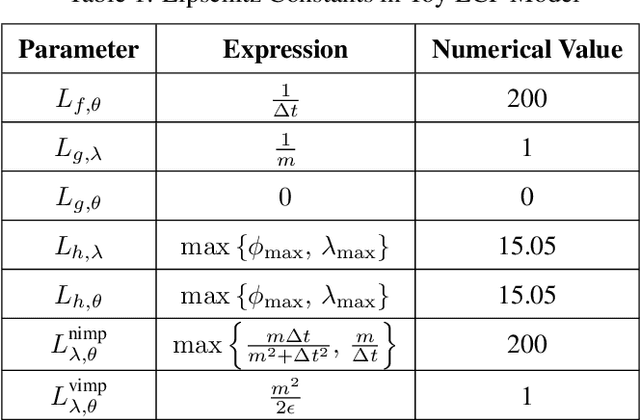
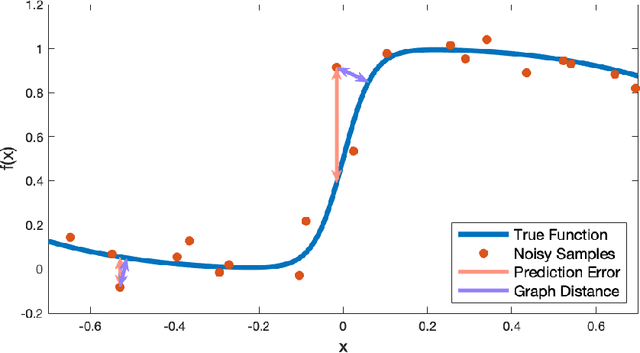
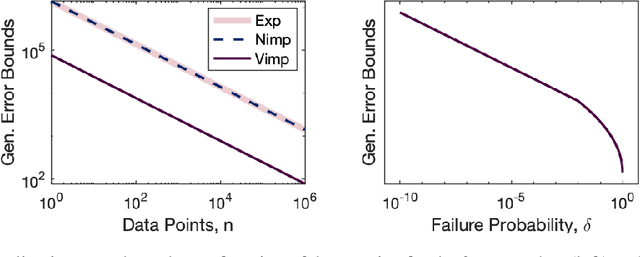
Abstract:Inspired by recent strides in empirical efficacy of implicit learning in many robotics tasks, we seek to understand the theoretical benefits of implicit formulations in the face of nearly discontinuous functions, common characteristics for systems that make and break contact with the environment such as in legged locomotion and manipulation. We present and motivate three formulations for learning a function: one explicit and two implicit. We derive generalization bounds for each of these three approaches, exposing where explicit and implicit methods alike based on prediction error losses typically fail to produce tight bounds, in contrast to other implicit methods with violation-based loss definitions that can be fundamentally more robust to steep slopes. Furthermore, we demonstrate that this violation implicit loss can tightly bound graph distance, a quantity that often has physical roots and handles noise in inputs and outputs alike, instead of prediction losses which consider output noise only. Our insights into the generalizability and physical relevance of violation implicit formulations match evidence from prior works and are validated through a toy problem, inspired by rigid-contact models and referenced throughout our theoretical analysis.
Set-Valued Rigid Body Dynamics for Simultaneous Frictional Impact
Apr 06, 2021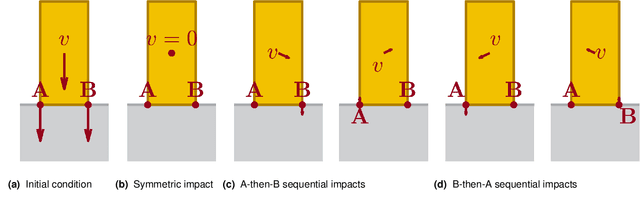

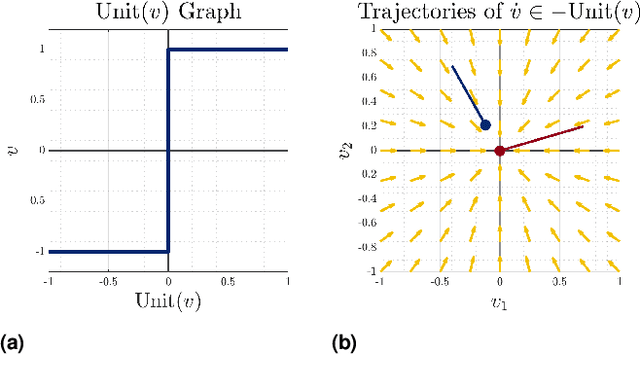

Abstract:Robotic manipulation and locomotion often entail nearly-simultaneous collisions -- such as heel and toe strikes during a foot step -- with outcomes that are extremely sensitive to the order in which impacts occur. Robotic simulators commonly lack the accuracy to predict this ordering, and instead pick one with a heuristic. This discrepancy degrades performance when model-based controllers and policies learned in simulation are placed on a real robot. We reconcile this issue with a set-valued rigid-body model which generates a broad set of physically reasonable outcomes of simultaneous frictional impacts. We first extend Routh's impact model to multiple impacts by reformulating it as a differential inclusion (DI), and show that any solution will resolve all impacts in finite time. By considering time as a state, we embed this model into another DI which captures the continuous-time evolution of rigid body dynamics, and guarantee existence of solutions. We finally cast simulation of simultaneous impacts as a linear complementarity problem (LCP), and develop an algorithm for tight approximation of the post-impact velocity set with probabilistic guarantees. We demonstrate our approach on several examples drawn from manipulation and legged locomotion.
Fundamental Challenges in Deep Learning for Stiff Contact Dynamics
Mar 29, 2021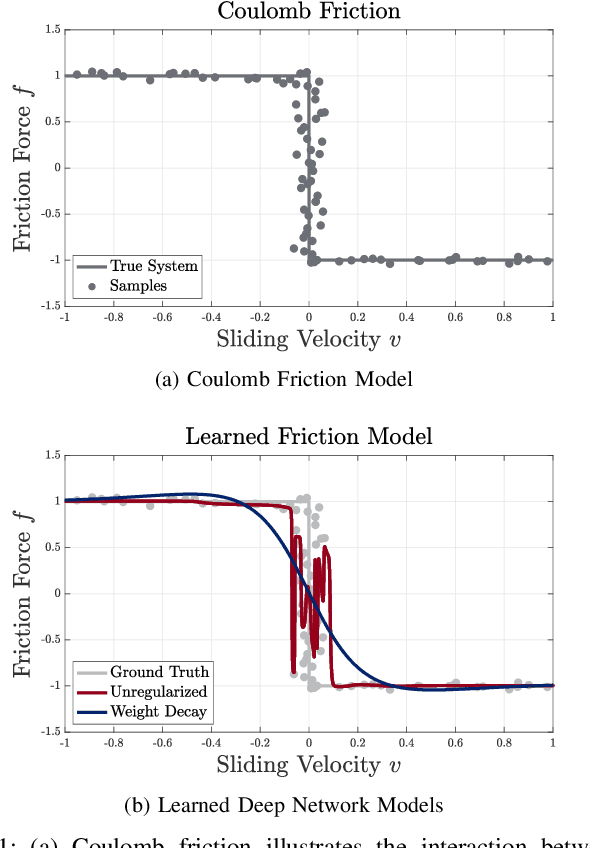

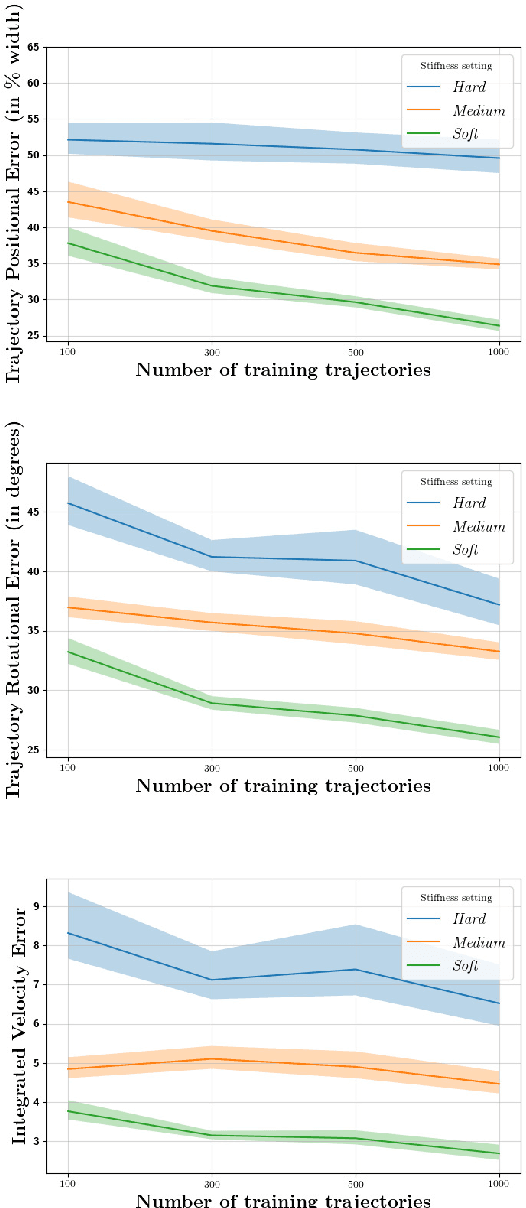
Abstract:Frictional contact has been extensively studied as the core underlying behavior of legged locomotion and manipulation, and its nearly-discontinuous nature makes planning and control difficult even when an accurate model of the robot is available. Here, we present empirical evidence that learning an accurate model in the first place can be confounded by contact, as modern deep learning approaches are not designed to capture this non-smoothness. We isolate the effects of contact's non-smoothness by varying the mechanical stiffness of a compliant contact simulator. Even for a simple system, we find that stiffness alone dramatically degrades training processes, generalization, and data-efficiency. Our results raise serious questions about simulated testing environments which do not accurately reflect the stiffness of rigid robotic hardware. Significant additional investigation will be necessary to fully understand and mitigate these effects, and we suggest several avenues for future study.
ContactNets: Learning of Discontinuous Contact Dynamics with Smooth, Implicit Representations
Sep 23, 2020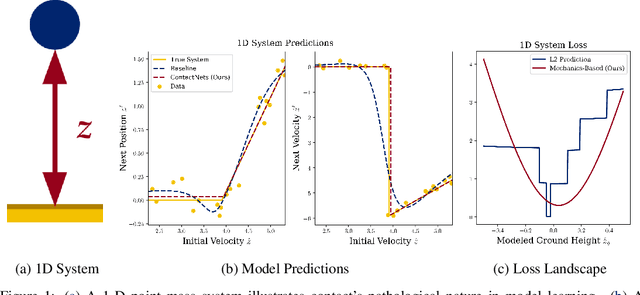
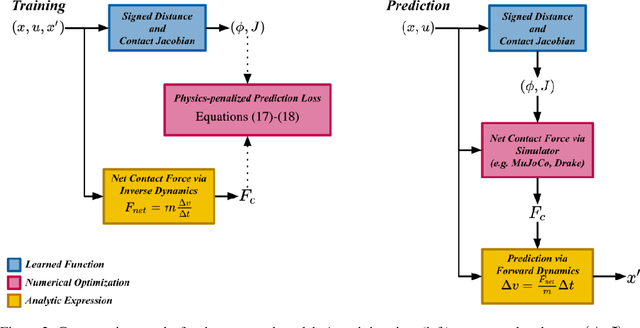


Abstract:Common methods for learning robot dynamics assume motion is continuous, causing unrealistic model predictions for systems undergoing discontinuous impact and stiction behavior. In this work, we resolve this conflict with a smooth, implicit encoding of the structure inherent to contact-induced discontinuities. Our method, ContactNets, learns parameterizations of inter-body signed distance and contact-frame Jacobians, a representation that is compatible with many simulation, control, and planning environments for robotics. We furthermore circumvent the need to differentiate through stiff or non-smooth dynamics with a novel loss function inspired by the principles of complementarity and maximum dissipation. Our method can predict realistic impact, non-penetration, and stiction when trained on 60 seconds of real-world data.
A Quasi-static Model and Simulation Approach for Pushing, Grasping, and Jamming
Feb 09, 2019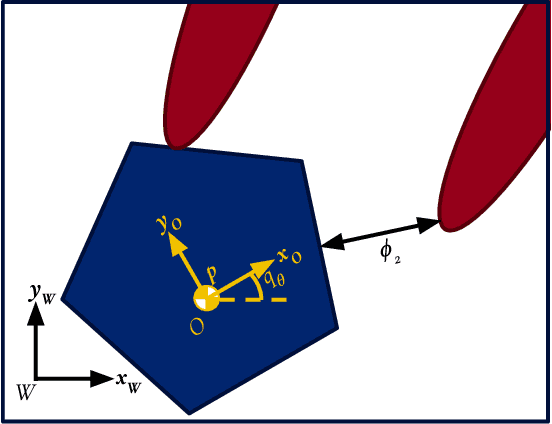
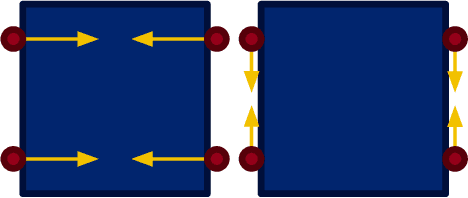
Abstract:Quasi-static models of robotic motion with frictional contact provide a computationally efficient framework for analysis and have been widely used for planning and control of non-prehensile manipulation. In this work, we present a novel quasi-static model of planar manipulation that directly maps commanded manipulator velocities to object motion. While quasi-static models have traditionally been unable to capture grasping and jamming behaviors, our approach solves this issue by explicitly modeling the limiting behavior of a velocity-controlled manipulator. We retain the precise modeling of surface contact pressure distributions and efficient computation of contact-rich behaviors of previous methods and additionally prove existence of solutions for any desired manipulator motion. We derive continuous and time-stepping formulations, both posed as tractable Linear Complementarity Problems (LCPs).
Modeling and Analysis of Non-unique Behaviors in Multiple Frictional Impacts
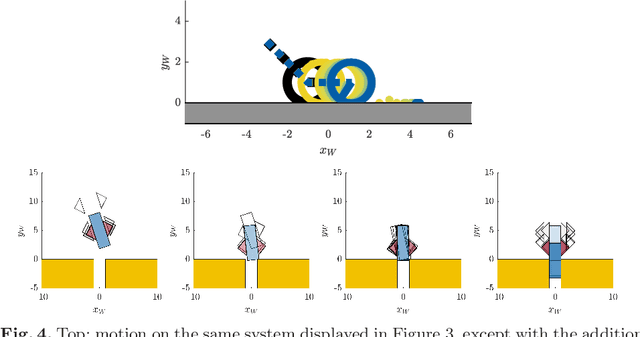
Feb 04, 2019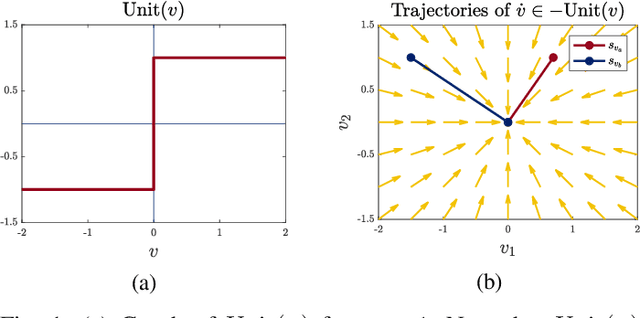
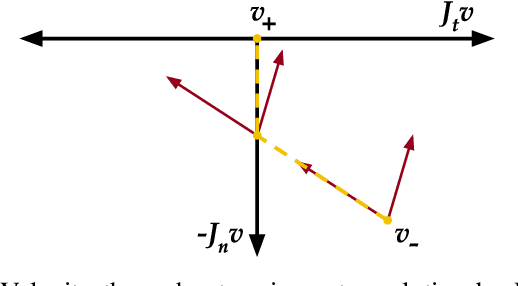
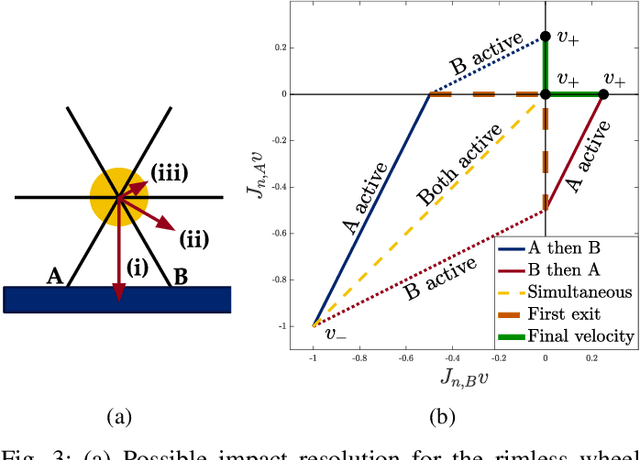
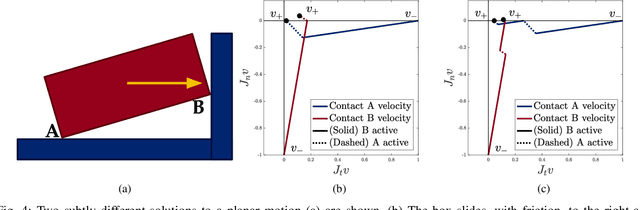
Abstract:Many fundamental challenges in robotics, based in manipulation or locomotion, require making and breaking contact with the environment. Models that address frictional contact must be inherently non-smooth; rigid-body models are especially popular, as they often lead to mathematically and computationally tractable approaches. However, when two or more impacts occur simultaneously, the precise sequencing of impact forces is generally unknown, leading to the potential for multiple possible outcomes. This simultaneity is far from pathological, and occurs in many common robotics applications. In this work, we present an approach to capturing simultaneous frictional impacts, represented as a differential inclusion. Solutions to our model, an extension to multiple contacts of Routh's graphical method, naturally capture the set of potential post-impact velocities. We prove that, under modest conditions, the presented approach is guaranteed to terminate. This is, to the best of our knowledge, the first such guarantee for simultaneous frictional impacts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge