A Quasi-static Model and Simulation Approach for Pushing, Grasping, and Jamming
Paper and Code
Feb 09, 2019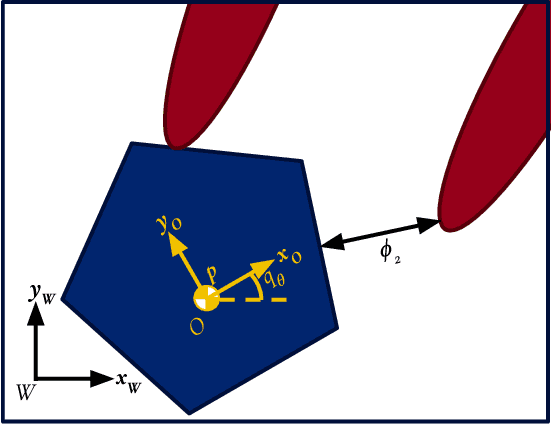
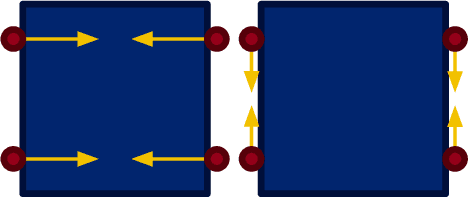
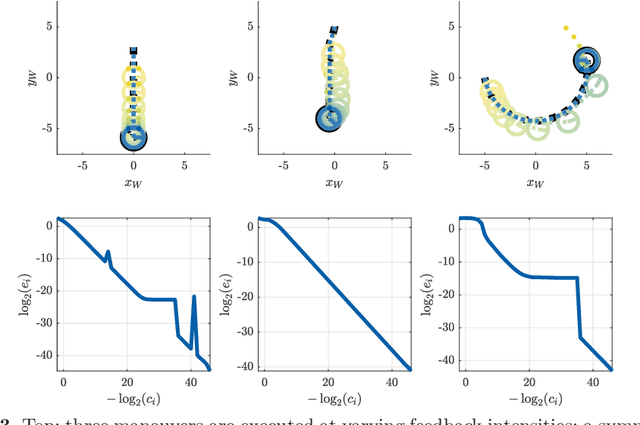
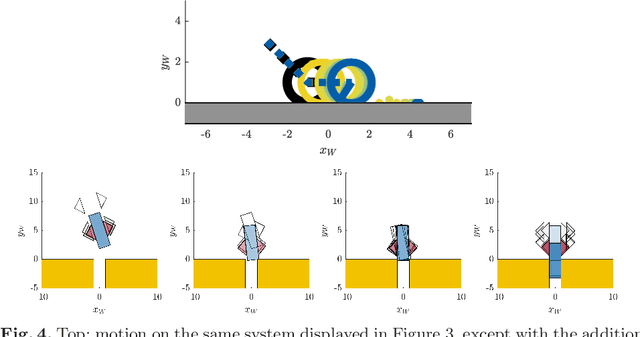
Quasi-static models of robotic motion with frictional contact provide a computationally efficient framework for analysis and have been widely used for planning and control of non-prehensile manipulation. In this work, we present a novel quasi-static model of planar manipulation that directly maps commanded manipulator velocities to object motion. While quasi-static models have traditionally been unable to capture grasping and jamming behaviors, our approach solves this issue by explicitly modeling the limiting behavior of a velocity-controlled manipulator. We retain the precise modeling of surface contact pressure distributions and efficient computation of contact-rich behaviors of previous methods and additionally prove existence of solutions for any desired manipulator motion. We derive continuous and time-stepping formulations, both posed as tractable Linear Complementarity Problems (LCPs).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge