Set-Valued Rigid Body Dynamics for Simultaneous Frictional Impact

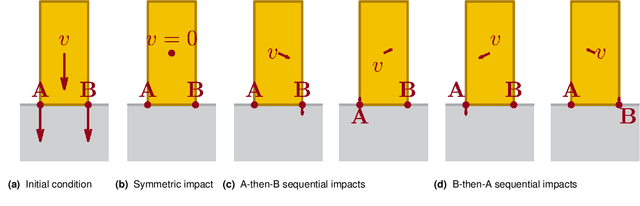
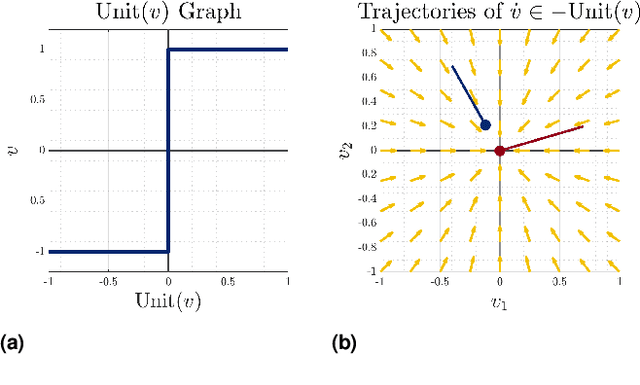
Robotic manipulation and locomotion often entail nearly-simultaneous collisions -- such as heel and toe strikes during a foot step -- with outcomes that are extremely sensitive to the order in which impacts occur. Robotic simulators commonly lack the accuracy to predict this ordering, and instead pick one with a heuristic. This discrepancy degrades performance when model-based controllers and policies learned in simulation are placed on a real robot. We reconcile this issue with a set-valued rigid-body model which generates a broad set of physically reasonable outcomes of simultaneous frictional impacts. We first extend Routh's impact model to multiple impacts by reformulating it as a differential inclusion (DI), and show that any solution will resolve all impacts in finite time. By considering time as a state, we embed this model into another DI which captures the continuous-time evolution of rigid body dynamics, and guarantee existence of solutions. We finally cast simulation of simultaneous impacts as a linear complementarity problem (LCP), and develop an algorithm for tight approximation of the post-impact velocity set with probabilistic guarantees. We demonstrate our approach on several examples drawn from manipulation and legged locomotion.