Learning Linear Complementarity Systems
Paper and Code
Dec 25, 2021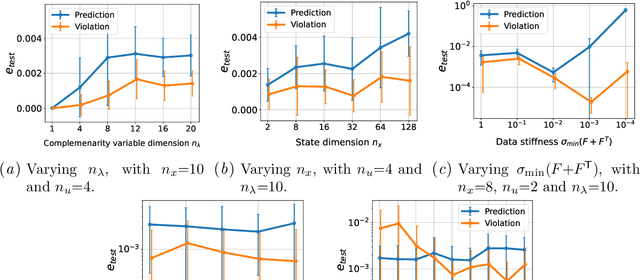
This paper investigates the learning, or system identification, of a class of piecewise-affine dynamical systems known as linear complementarity systems (LCSs). We propose a violation-based loss which enables efficient learning of the LCS parameterization, without prior knowledge of the hybrid mode boundaries, using gradient-based methods. The proposed violation-based loss incorporates both dynamics prediction loss and a novel complementarity - violation loss. We show several properties attained by this loss formulation, including its differentiability, the efficient computation of first- and second-order derivatives, and its relationship to the traditional prediction loss, which strictly enforces complementarity. We apply this violation-based loss formulation to learn LCSs with tens of thousands of (potentially stiff) hybrid modes. The results demonstrate a state-of-the-art ability to identify piecewise-affine dynamics, outperforming methods which must differentiate through non-smooth linear complementarity problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge