A Mean-Field Theory for Learning the Schönberg Measure of Radial Basis Functions

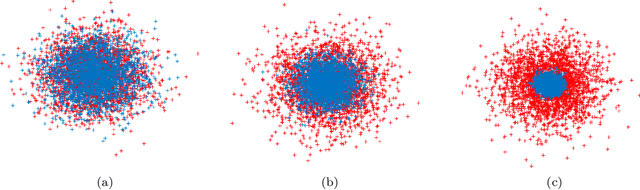
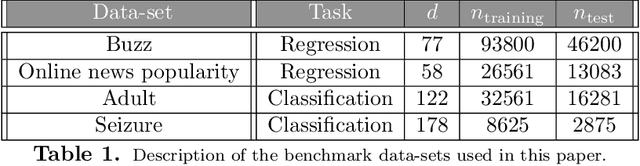
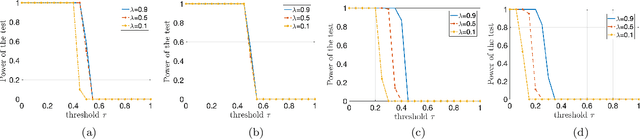
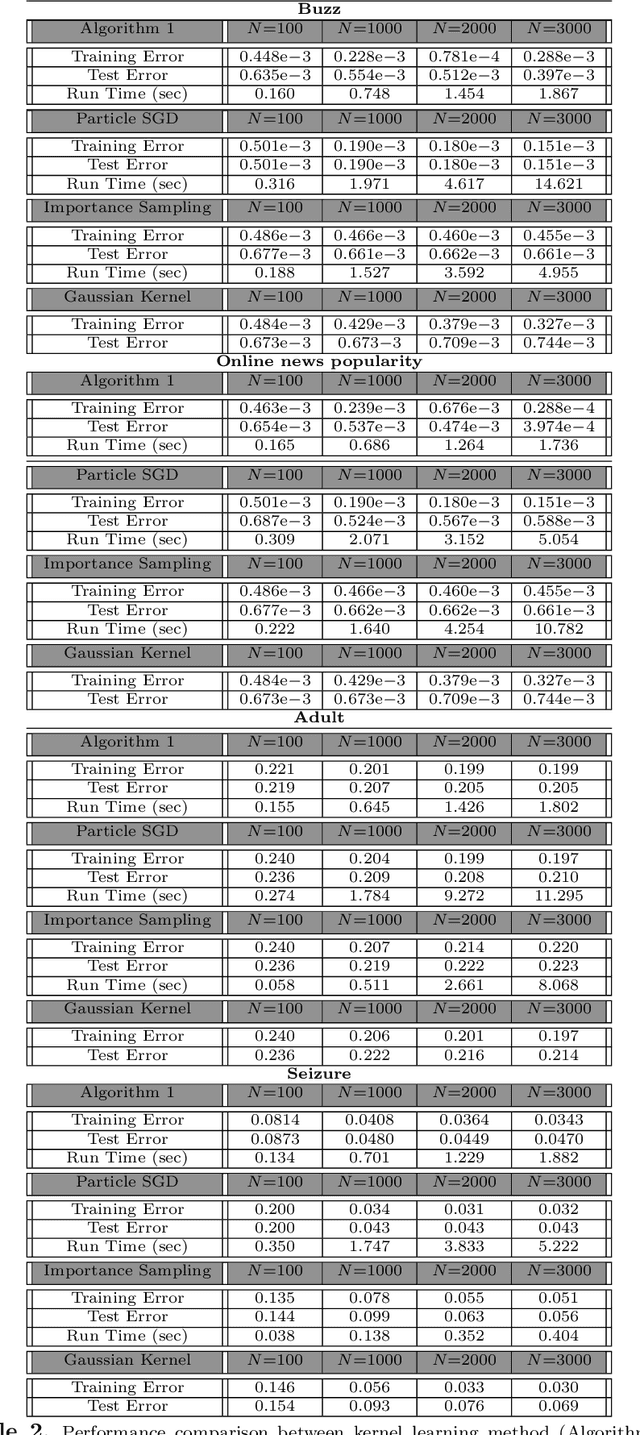
We develop and analyze a projected particle Langevin optimization method to learn the distribution in the Sch\"{o}nberg integral representation of the radial basis functions from training samples. More specifically, we characterize a distributionally robust optimization method with respect to the Wasserstein distance to optimize the distribution in the Sch\"{o}nberg integral representation. To provide theoretical performance guarantees, we analyze the scaling limits of a projected particle online (stochastic) optimization method in the mean-field regime. In particular, we prove that in the scaling limits, the empirical measure of the Langevin particles converges to the law of a reflected It\^{o} diffusion-drift process. Moreover, the drift is also a function of the law of the underlying process. Using It\^{o} lemma for semi-martingales and Grisanov's change of measure for the Wiener processes, we then derive a Mckean-Vlasov type partial differential equation (PDE) with Robin boundary conditions that describes the evolution of the empirical measure of the projected Langevin particles in the mean-field regime. In addition, we establish the existence and uniqueness of the steady-state solutions of the derived PDE in the weak sense. We apply our learning approach to train radial kernels in the kernel locally sensitive hash (LSH) functions, where the training data-set is generated via a $k$-mean clustering method on a small subset of data-base. We subsequently apply our kernel LSH with a trained kernel for image retrieval task on MNIST data-set, and demonstrate the efficacy of our kernel learning approach. We also apply our kernel learning approach in conjunction with the kernel support vector machines (SVMs) for classification of benchmark data-sets.

Machine Learning Techniques for Biomedical Image Segmentation: An Overview of Technical Aspects and Introduction to State-of-Art Applications

In recent years, significant progress has been made in developing more accurate and efficient machine learning algorithms for segmentation of medical and natural images. In this review article, we highlight the imperative role of machine learning algorithms in enabling efficient and accurate segmentation in the field of medical imaging. We specifically focus on several key studies pertaining to the application of machine learning methods to biomedical image segmentation. We review classical machine learning algorithms such as Markov random fields, k-means clustering, random forest, etc. Although such classical learning models are often less accurate compared to the deep learning techniques, they are often more sample efficient and have a less complex structure. We also review different deep learning architectures, such as the artificial neural networks (ANNs), the convolutional neural networks (CNNs), and the recurrent neural networks (RNNs), and present the segmentation results attained by those learning models that were published in the past three years. We highlight the successes and limitations of each machine learning paradigm. In addition, we discuss several challenges related to the training of different machine learning models, and we present some heuristics to address those challenges.

A Mean-Field Theory for Kernel Alignment with Random Features in Generative Adversarial Networks

We propose a novel supervised learning method to optimize the kernel in maximum mean discrepancy generative adversarial networks (MMD GANs). Specifically, we characterize a distributionally robust optimization problem to compute a good distribution for the random feature model of Rahimi and Recht to approximate a good kernel function. Due to the fact that the distributional optimization is infinite dimensional, we consider a Monte-Carlo sample average approximation (SAA) to obtain a more tractable finite dimensional optimization problem. We subsequently leverage a particle stochastic gradient descent (SGD) method to solve finite dimensional optimization problems. Based on a mean-field analysis, we then prove that the empirical distribution of the interactive particles system at each iteration of the SGD follows the path of the gradient descent flow on the Wasserstein manifold. We also establish the non-asymptotic consistency of the finite sample estimator. Our empirical evaluation on synthetic data-set as well as MNIST and CIFAR-10 benchmark data-sets indicates that our proposed MMD GAN model with kernel learning indeed attains higher inception scores well as Fr\`{e}chet inception distances and generates better images compared to the generative moment matching network (GMMN) and MMD GAN with untrained kernels.

On Sample Complexity of Projection-Free Primal-Dual Methods for Learning Mixture Policies in Markov Decision Processes

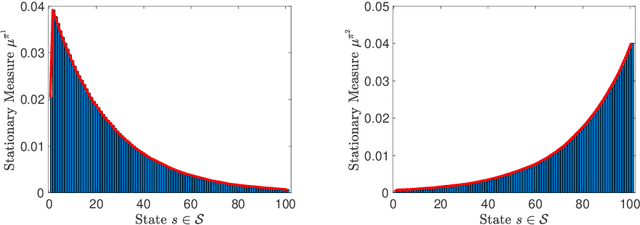
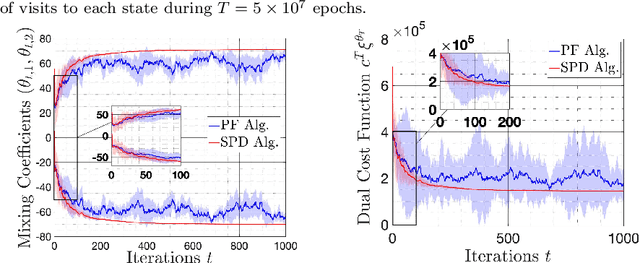
We study the problem of learning policy of an infinite-horizon, discounted cost, Markov decision process (MDP) with a large number of states. We compute the actions of a policy that is nearly as good as a policy chosen by a suitable oracle from a given mixture policy class characterized by the convex hull of a set of known base policies. To learn the coefficients of the mixture model, we recast the problem as an approximate linear programming (ALP) formulation for MDPs, where the feature vectors correspond to the occupation measures of the base policies defined on the state-action space. We then propose a projection-free stochastic primal-dual method with the Bregman divergence to solve the characterized ALP. Furthermore, we analyze the probably approximately correct (PAC) sample complexity of the proposed stochastic algorithm, namely the number of queries required to achieve near optimal objective value. We also propose a modification of our proposed algorithm with the polytope constraint sampling for the smoothed ALP, where the restriction to lower bounding approximations are relaxed. In addition, we apply the proposed algorithms to a queuing problem, and compare their performance with a penalty function algorithm. The numerical results illustrates that the primal-dual achieves better efficiency and low variance across different trials compared to the penalty function method.

Multiple Kernel Learning from $U$-Statistics of Empirical Measures in the Feature Space

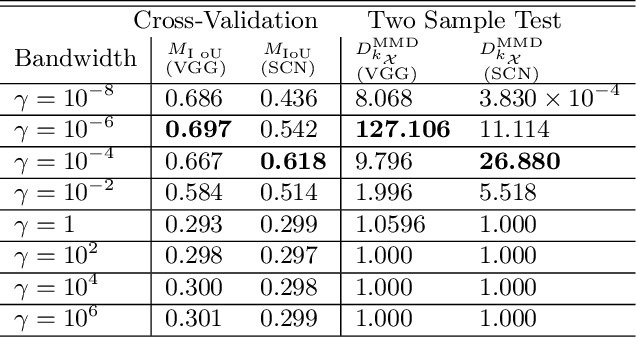
We propose a novel data-driven method to learn multiple kernels in kernel methods of statistical machine learning from training samples. The proposed kernel learning algorithm is based on a $U$-statistics of the empirical marginal distributions of features in the feature space given their class labels. We prove the consistency of the $U$-statistic estimate using the empirical distributions for kernel learning. In particular, we show that the empirical estimate of $U$-statistic converges to its population value with respect to all admissible distributions as the number of the training samples increase. We also prove the sample optimality of the estimate by establishing a minimax lower bound via Fano's method. In addition, we establish the generalization bounds of the proposed kernel learning approach by computing novel upper bounds on the Rademacher and Gaussian complexities using the concentration of measures for the quadratic matrix forms.We apply the proposed kernel learning approach to classification of the real-world data-sets using the kernel SVM and compare the results with $5$-fold cross-validation for the kernel model selection problem. We also apply the proposed kernel learning approach to devise novel architectures for the semantic segmentation of biomedical images. The proposed segmentation networks are suited for training on small data-sets and employ new mechanisms to generate representations from input images.