Multiple Kernel Learning from $U$-Statistics of Empirical Measures in the Feature Space
Paper and Code
Feb 27, 2019


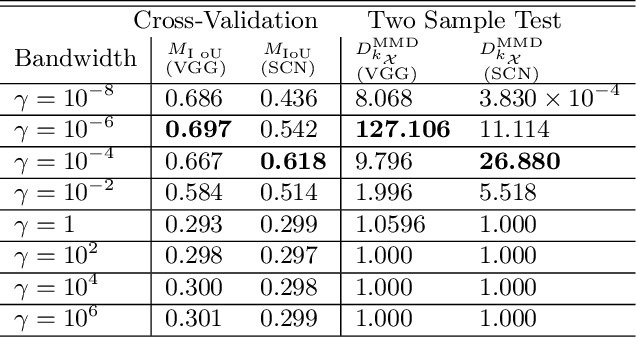
We propose a novel data-driven method to learn multiple kernels in kernel methods of statistical machine learning from training samples. The proposed kernel learning algorithm is based on a $U$-statistics of the empirical marginal distributions of features in the feature space given their class labels. We prove the consistency of the $U$-statistic estimate using the empirical distributions for kernel learning. In particular, we show that the empirical estimate of $U$-statistic converges to its population value with respect to all admissible distributions as the number of the training samples increase. We also prove the sample optimality of the estimate by establishing a minimax lower bound via Fano's method. In addition, we establish the generalization bounds of the proposed kernel learning approach by computing novel upper bounds on the Rademacher and Gaussian complexities using the concentration of measures for the quadratic matrix forms.We apply the proposed kernel learning approach to classification of the real-world data-sets using the kernel SVM and compare the results with $5$-fold cross-validation for the kernel model selection problem. We also apply the proposed kernel learning approach to devise novel architectures for the semantic segmentation of biomedical images. The proposed segmentation networks are suited for training on small data-sets and employ new mechanisms to generate representations from input images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge