Signed Diverse Multiplex Networks: Clustering and Inference

The paper introduces a Signed Generalized Random Dot Product Graph (SGRDPG) model, which is a variant of the Generalized Random Dot Product Graph (GRDPG), where, in addition, edges can be positive or negative. The setting is extended to a multiplex version, where all layers have the same collection of nodes and follow the SGRDPG. The only common feature of the layers of the network is that they can be partitioned into groups with common subspace structures, while otherwise all matrices of connection probabilities can be all different. The setting above is extremely flexible and includes a variety of existing multiplex network models as its particular cases. The paper fulfills two objectives. First, it shows that keeping signs of the edges in the process of network construction leads to a better precision of estimation and clustering and, hence, is beneficial for tackling real world problems such as analysis of brain networks. Second, by employing novel algorithms, our paper ensures equivalent or superior accuracy than has been achieved in simpler multiplex network models. In addition to theoretical guarantees, both of those features are demonstrated using numerical simulations and a real data example.

Sparse Subspace Clustering in Diverse Multiplex Network Model

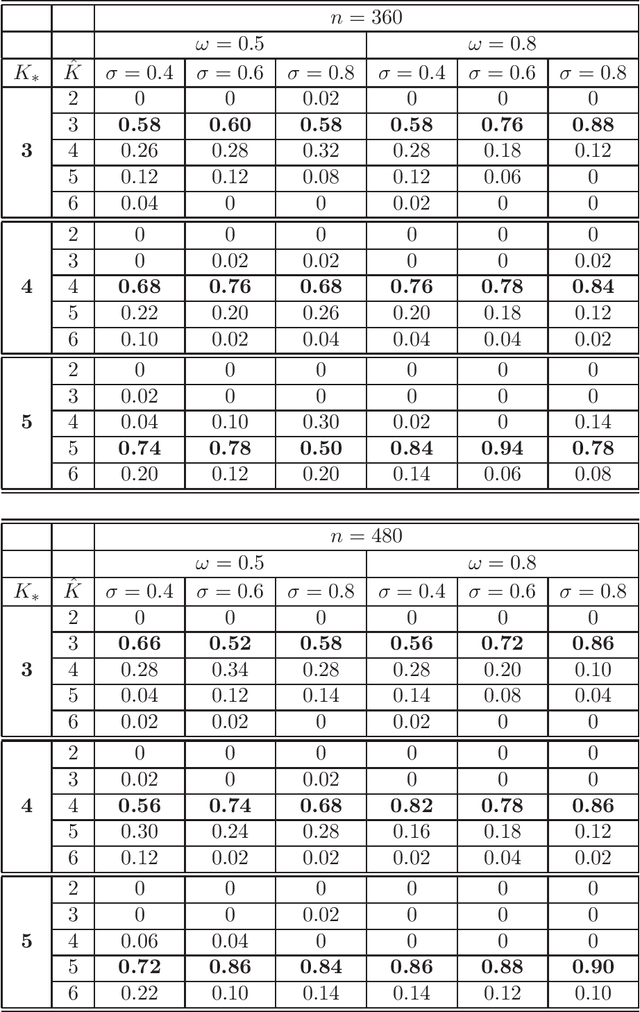
The paper considers the DIverse MultiPLEx (DIMPLE) network model, introduced in Pensky and Wang (2021), where all layers of the network have the same collection of nodes and are equipped with the Stochastic Block Models. In addition, all layers can be partitioned into groups with the same community structures, although the layers in the same group may have different matrices of block connection probabilities. The DIMPLE model generalizes a multitude of papers that study multilayer networks with the same community structures in all layers, as well as the Mixture Multilayer Stochastic Block Model (MMLSBM), where the layers in the same group have identical matrices of block connection probabilities. While Pensky and Wang (2021) applied spectral clustering to the proxy of the adjacency tensor, the present paper uses Sparse Subspace Clustering (SSC) for identifying groups of layers with identical community structures. Under mild conditions, the latter leads to the strongly consistent between-layer clustering. In addition, SSC allows to handle much larger networks than methodology of Pensky and Wang (2021), and is perfectly suitable for application of parallel computing.

ALMA: Alternating Minimization Algorithm for Clustering Mixture Multilayer Network

The paper considers a Mixture Multilayer Stochastic Block Model (MMLSBM), where layers can be partitioned into groups of similar networks, and networks in each group are equipped with a distinct Stochastic Block Model. The goal is to partition the multilayer network into clusters of similar layers, and to identify communities in those layers. Jing et al. (2020) introduced the MMLSBM and developed a clustering methodology, TWIST, based on regularized tensor decomposition. The present paper proposes a different technique, an alternating minimization algorithm (ALMA), that aims at simultaneous recovery of the layer partition, together with estimation of the matrices of connection probabilities of the distinct layers. Compared to TWIST, ALMA achieves higher accuracy both theoretically and numerically.

Statistical Inference in Heterogeneous Block Model

There exist various types of network block models such as the Stochastic Block Model (SBM), the Degree Corrected Block Model (DCBM), and the Popularity Adjusted Block Model (PABM). While this leads to a variety of choices, the block models do not have a nested structure. In addition, there is a substantial jump in the number of parameters from the DCBM to the PABM. The objective of this paper is formulation of a hierarchy of block model which does not rely on arbitrary identifiability conditions, treats the SBM, the DCBM and the PABM as its particular cases with specific parameter values and, in addition, allows a multitude of versions that are more complicated than DCBM but have fewer unknown parameters than the PABM. The latter allows one to carry out clustering and estimation without preliminary testing to see which block model is really true.

Sparse Popularity Adjusted Stochastic Block Model

The objective of the present paper is to study the Popularity Adjusted Block Model (PABM) in the sparse setting. Unlike in other block models, the flexibility of PABM allows to set some of the connection probabilities to zero while maintaining the rest of the probabilities non-negligible, leading to the Sparse Popularity Adjusted Block Model (SPABM). The latter reduces the size of parameter set and leads to improved precision of estimation and clustering. The theory is complemented by the simulation study and real data examples.

Sparse One-Time Grab Sampling of Inliers

Estimating structures in "big data" and clustering them are among the most fundamental problems in computer vision, pattern recognition, data mining, and many other other research fields. Over the past few decades, many studies have been conducted focusing on different aspects of these problems. One of the main approaches that is explored in the literature to tackle the problems of size and dimensionality is sampling subsets of the data in order to estimate the characteristics of the whole population, e.g. estimating the underlying clusters or structures in the data. In this paper, we propose a `one-time-grab' sampling algorithm\cite{jaberi2015swift,jaberi2018sparse}. This method can be used as the front end to any supervised or unsupervised clustering method. Rather than focusing on the strategy of maximizing the probability of sampling inliers, our goal is to minimize the number of samples needed to instantiate all underlying model instances. More specifically, our goal is to answer the following question: {\em `Given a very large population of points with $C$ embedded structures and gross outliers, what is the minimum number of points $r$ to be selected randomly in one grab in order to make sure with probability $P$ that at least $\varepsilon$ points are selected on each structure, where $\varepsilon$ is the number of degrees of freedom of each structure.'}

Probabilistic Sparse Subspace Clustering Using Delayed Association

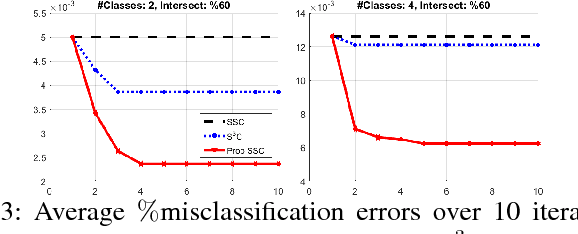
Discovering and clustering subspaces in high-dimensional data is a fundamental problem of machine learning with a wide range of applications in data mining, computer vision, and pattern recognition. Earlier methods divided the problem into two separate stages of finding the similarity matrix and finding clusters. Similar to some recent works, we integrate these two steps using a joint optimization approach. We make the following contributions: (i) we estimate the reliability of the cluster assignment for each point before assigning a point to a subspace. We group the data points into two groups of "certain" and "uncertain", with the assignment of latter group delayed until their subspace association certainty improves. (ii) We demonstrate that delayed association is better suited for clustering subspaces that have ambiguities, i.e. when subspaces intersect or data are contaminated with outliers/noise. (iii) We demonstrate experimentally that such delayed probabilistic association leads to a more accurate self-representation and final clusters. The proposed method has higher accuracy both for points that exclusively lie in one subspace, and those that are on the intersection of subspaces. (iv) We show that delayed association leads to huge reduction of computational cost, since it allows for incremental spectral clustering.

Classification with many classes: challenges and pluses

The objective of the paper is to study accuracy of multi-class classification in high-dimensional setting, where the number of classes is also large ("large $L$, large $p$, small $n$" model). While this problem arises in many practical applications and many techniques have been recently developed for its solution, to the best of our knowledge nobody provided a rigorous theoretical analysis of this important setup. The purpose of the present paper is to fill in this gap. We consider one of the most common settings, classification of high-dimensional normal vectors where, unlike standard assumptions, the number of classes could be large. We derive non-asymptotic conditions on effects of significant features, and the low and the upper bounds for distances between classes required for successful feature selection and classification with a given accuracy. Furthermore, we study an asymptotic setup where the number of classes is growing with the dimension of feature space and while the number of samples per class is possibly limited. We discover an interesting and, at first glance, somewhat counter-intuitive phenomenon that a large number of classes may be a "blessing" rather than a "curse" since, in certain settings, the precision of classification can improve as the number of classes grows. This is due to more accurate feature selection since even weaker significant features, which are not sufficiently strong to be manifested in a coarse classification, can nevertheless have a strong impact when the number of classes is large. We supplement our theoretical investigation by a simulation study and a real data example where we again observe the above phenomenon.

Solution of linear ill-posed problems using random dictionaries

In the present paper we consider application of overcomplete dictionaries to solution of general ill-posed linear inverse problems. In the context of regression problems, there has been enormous amount of effort to recover an unknown function using such dictionaries. One of the most popular methods, lasso and its versions, is based on minimizing empirical likelihood and unfortunately, requires stringent assumptions on the dictionary, the, so called, compatibility conditions. Though compatibility conditions are hard to satisfy, it is well known that this can be accomplished by using random dictionaries. In the present paper, we show how one can apply random dictionaries to solution of ill-posed linear inverse problems. We put a theoretical foundation under the suggested methodology and study its performance via simulations.

Spectral clustering in the dynamic stochastic block model

In the present paper, we studied a Dynamic Stochastic Block Model (DSBM) under the assumptions that the connection probabilities, as functions of time, are smooth and that at most $s$ nodes can switch their class memberships between two consecutive time points. We estimate the edge probability tensor by a kernel-type procedure and extract the group memberships of the nodes by spectral clustering. The procedure is computationally viable, adaptive to the unknown smoothness of the functional connection probabilities, to the rate $s$ of membership switching and to the unknown number of clusters. In addition, it is accompanied by non-asymptotic guarantees for the precision of estimation and clustering.