Sparse Popularity Adjusted Stochastic Block Model
Paper and Code
Oct 03, 2019
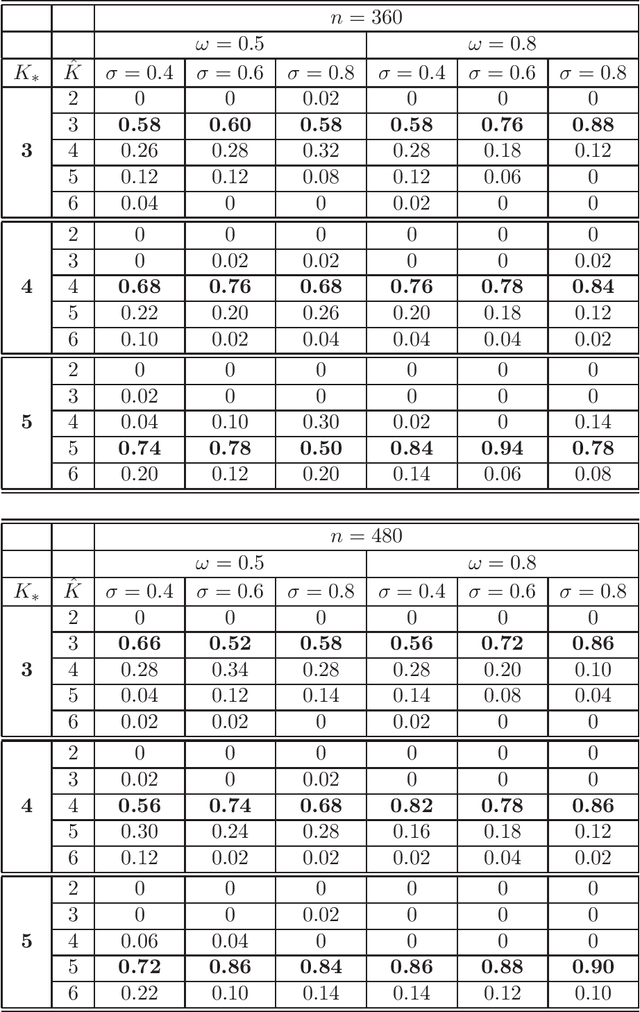


The objective of the present paper is to study the Popularity Adjusted Block Model (PABM) in the sparse setting. Unlike in other block models, the flexibility of PABM allows to set some of the connection probabilities to zero while maintaining the rest of the probabilities non-negligible, leading to the Sparse Popularity Adjusted Block Model (SPABM). The latter reduces the size of parameter set and leads to improved precision of estimation and clustering. The theory is complemented by the simulation study and real data examples.
* 4 figures. arXiv admin note: text overlap with arXiv:1902.00431
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge