Sparse Subspace Clustering in Diverse Multiplex Network Model

The paper considers the DIverse MultiPLEx (DIMPLE) network model, introduced in Pensky and Wang (2021), where all layers of the network have the same collection of nodes and are equipped with the Stochastic Block Models. In addition, all layers can be partitioned into groups with the same community structures, although the layers in the same group may have different matrices of block connection probabilities. The DIMPLE model generalizes a multitude of papers that study multilayer networks with the same community structures in all layers, as well as the Mixture Multilayer Stochastic Block Model (MMLSBM), where the layers in the same group have identical matrices of block connection probabilities. While Pensky and Wang (2021) applied spectral clustering to the proxy of the adjacency tensor, the present paper uses Sparse Subspace Clustering (SSC) for identifying groups of layers with identical community structures. Under mild conditions, the latter leads to the strongly consistent between-layer clustering. In addition, SSC allows to handle much larger networks than methodology of Pensky and Wang (2021), and is perfectly suitable for application of parallel computing.

Statistical Inference in Heterogeneous Block Model

There exist various types of network block models such as the Stochastic Block Model (SBM), the Degree Corrected Block Model (DCBM), and the Popularity Adjusted Block Model (PABM). While this leads to a variety of choices, the block models do not have a nested structure. In addition, there is a substantial jump in the number of parameters from the DCBM to the PABM. The objective of this paper is formulation of a hierarchy of block model which does not rely on arbitrary identifiability conditions, treats the SBM, the DCBM and the PABM as its particular cases with specific parameter values and, in addition, allows a multitude of versions that are more complicated than DCBM but have fewer unknown parameters than the PABM. The latter allows one to carry out clustering and estimation without preliminary testing to see which block model is really true.

Sparse Popularity Adjusted Stochastic Block Model

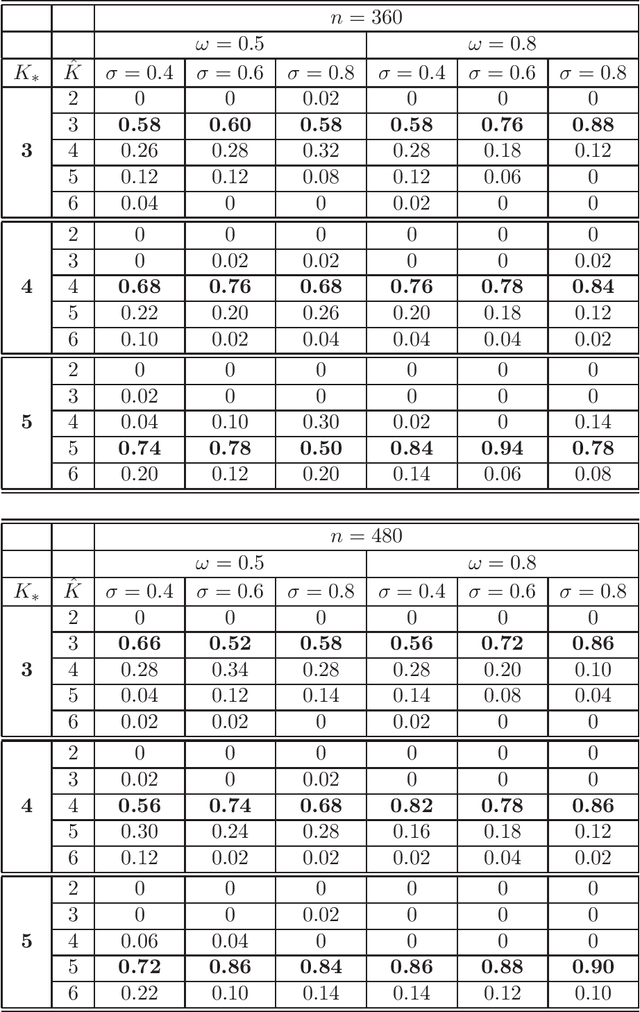
The objective of the present paper is to study the Popularity Adjusted Block Model (PABM) in the sparse setting. Unlike in other block models, the flexibility of PABM allows to set some of the connection probabilities to zero while maintaining the rest of the probabilities non-negligible, leading to the Sparse Popularity Adjusted Block Model (SPABM). The latter reduces the size of parameter set and leads to improved precision of estimation and clustering. The theory is complemented by the simulation study and real data examples.