Maryam Jaberi
Sparse One-Time Grab Sampling of Inliers
Dec 21, 2018Abstract:Estimating structures in "big data" and clustering them are among the most fundamental problems in computer vision, pattern recognition, data mining, and many other other research fields. Over the past few decades, many studies have been conducted focusing on different aspects of these problems. One of the main approaches that is explored in the literature to tackle the problems of size and dimensionality is sampling subsets of the data in order to estimate the characteristics of the whole population, e.g. estimating the underlying clusters or structures in the data. In this paper, we propose a `one-time-grab' sampling algorithm\cite{jaberi2015swift,jaberi2018sparse}. This method can be used as the front end to any supervised or unsupervised clustering method. Rather than focusing on the strategy of maximizing the probability of sampling inliers, our goal is to minimize the number of samples needed to instantiate all underlying model instances. More specifically, our goal is to answer the following question: {\em `Given a very large population of points with $C$ embedded structures and gross outliers, what is the minimum number of points $r$ to be selected randomly in one grab in order to make sure with probability $P$ that at least $\varepsilon$ points are selected on each structure, where $\varepsilon$ is the number of degrees of freedom of each structure.'}
Probabilistic Sparse Subspace Clustering Using Delayed Association
Aug 28, 2018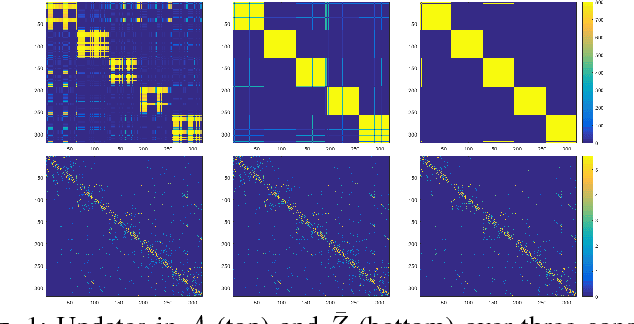

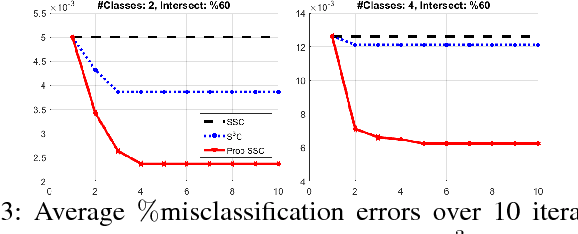

Abstract:Discovering and clustering subspaces in high-dimensional data is a fundamental problem of machine learning with a wide range of applications in data mining, computer vision, and pattern recognition. Earlier methods divided the problem into two separate stages of finding the similarity matrix and finding clusters. Similar to some recent works, we integrate these two steps using a joint optimization approach. We make the following contributions: (i) we estimate the reliability of the cluster assignment for each point before assigning a point to a subspace. We group the data points into two groups of "certain" and "uncertain", with the assignment of latter group delayed until their subspace association certainty improves. (ii) We demonstrate that delayed association is better suited for clustering subspaces that have ambiguities, i.e. when subspaces intersect or data are contaminated with outliers/noise. (iii) We demonstrate experimentally that such delayed probabilistic association leads to a more accurate self-representation and final clusters. The proposed method has higher accuracy both for points that exclusively lie in one subspace, and those that are on the intersection of subspaces. (iv) We show that delayed association leads to huge reduction of computational cost, since it allows for incremental spectral clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge