Probabilistic Sparse Subspace Clustering Using Delayed Association
Paper and Code
Aug 28, 2018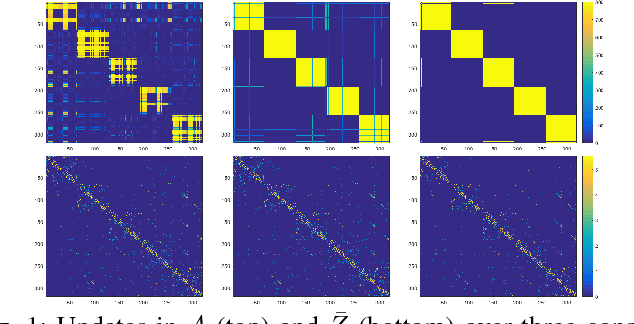

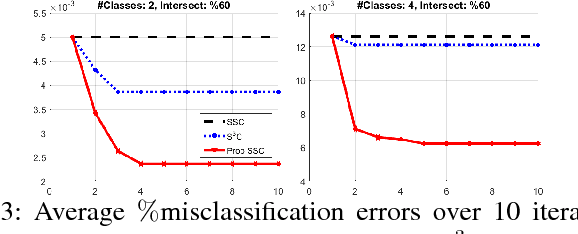

Discovering and clustering subspaces in high-dimensional data is a fundamental problem of machine learning with a wide range of applications in data mining, computer vision, and pattern recognition. Earlier methods divided the problem into two separate stages of finding the similarity matrix and finding clusters. Similar to some recent works, we integrate these two steps using a joint optimization approach. We make the following contributions: (i) we estimate the reliability of the cluster assignment for each point before assigning a point to a subspace. We group the data points into two groups of "certain" and "uncertain", with the assignment of latter group delayed until their subspace association certainty improves. (ii) We demonstrate that delayed association is better suited for clustering subspaces that have ambiguities, i.e. when subspaces intersect or data are contaminated with outliers/noise. (iii) We demonstrate experimentally that such delayed probabilistic association leads to a more accurate self-representation and final clusters. The proposed method has higher accuracy both for points that exclusively lie in one subspace, and those that are on the intersection of subspaces. (iv) We show that delayed association leads to huge reduction of computational cost, since it allows for incremental spectral clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge