Guaranteed Conservation of Momentum for Learning Particle-based Fluid Dynamics

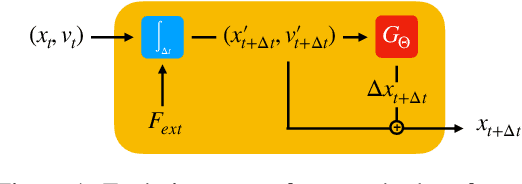
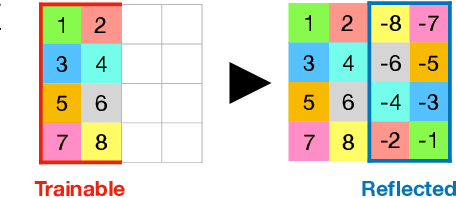
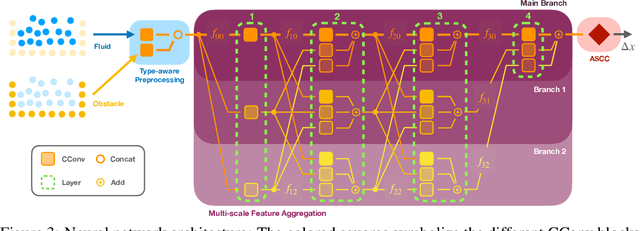
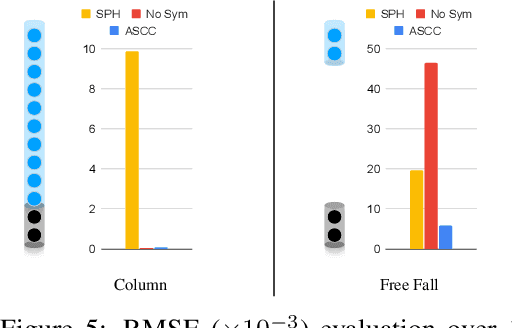
We present a novel method for guaranteeing linear momentum in learned physics simulations. Unlike existing methods, we enforce conservation of momentum with a hard constraint, which we realize via antisymmetrical continuous convolutional layers. We combine these strict constraints with a hierarchical network architecture, a carefully constructed resampling scheme, and a training approach for temporal coherence. In combination, the proposed method allows us to increase the physical accuracy of the learned simulator substantially. In addition, the induced physical bias leads to significantly better generalization performance and makes our method more reliable in unseen test cases. We evaluate our method on a range of different, challenging fluid scenarios. Among others, we demonstrate that our approach generalizes to new scenarios with up to one million particles. Our results show that the proposed algorithm can learn complex dynamics while outperforming existing approaches in generalization and training performance. An implementation of our approach is available at https://github.com/tum-pbs/DMCF.

Wavelet-based Loss for High-frequency Interface Dynamics

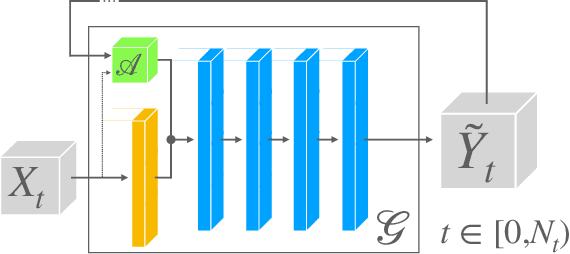
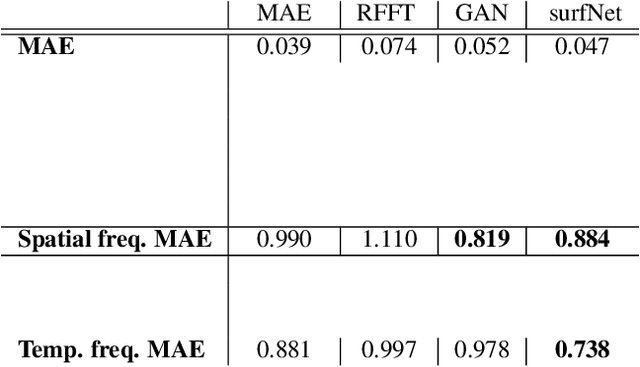
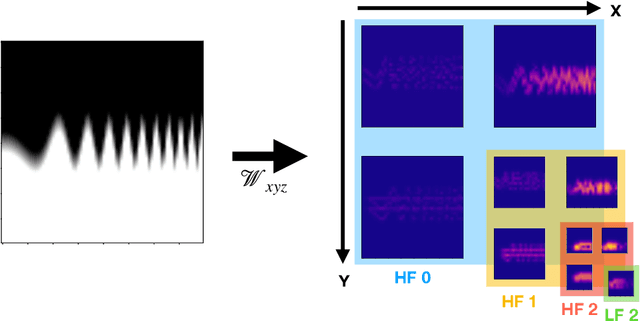
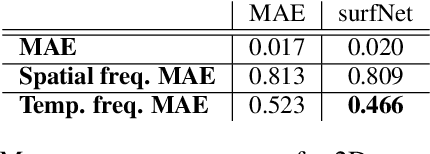
Generating highly detailed, complex data is a long-standing and frequently considered problem in the machine learning field. However, developing detail-aware generators remains an challenging and open problem. Generative adversarial networks are the basis of many state-of-the-art methods. However, they introduce a second network to be trained as a loss function, making the interpretation of the learned functions much more difficult. As an alternative, we present a new method based on a wavelet loss formulation, which remains transparent in terms of what is optimized. The wavelet-based loss function is used to overcome the limitations of conventional distance metrics, such as L1 or L2 distances, when it comes to generate data with high-frequency details. We show that our method can successfully reconstruct high-frequency details in an illustrative synthetic test case. Additionally, we evaluate the performance when applied to more complex surfaces based on physical simulations. Taking a roughly approximated simulation as input, our method infers corresponding spatial details while taking into account how they evolve. We consider this problem in terms of spatial and temporal frequencies, and leverage generative networks trained with our wavelet loss to learn the desired spatio-temporal signal for the surface dynamics. We test the capabilities of our method with a set of synthetic wave function tests and complex 2D and 3D dynamics of elasto-plastic materials.

Learning the shape of female breasts: an open-access 3D statistical shape model of the female breast built from 110 breast scans

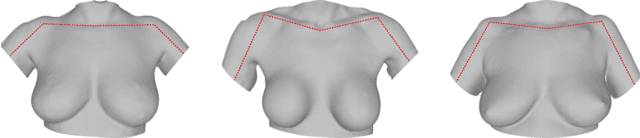
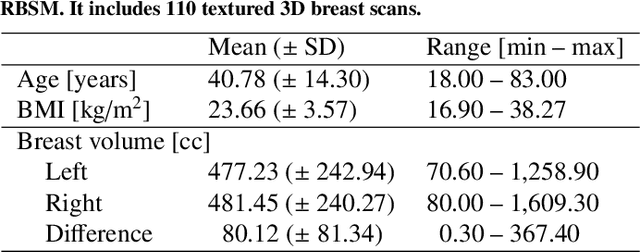
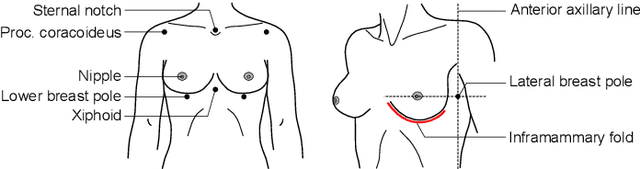
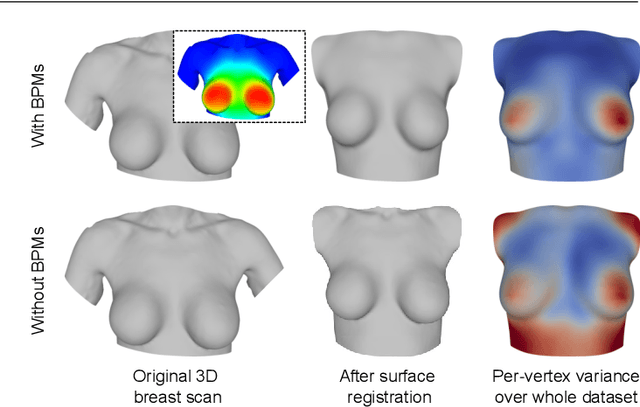
We present the Regensburg Breast Shape Model (RBSM) - a 3D statistical shape model of the female breast built from 110 breast scans, and the first ever publicly available. Together with the model, a fully automated, pairwise surface registration pipeline used to establish correspondence among 3D breast scans is introduced. Our method is computationally efficient and requires only four landmarks to guide the registration process. In order to weaken the strong coupling between breast and thorax, we propose to minimize the variance outside the breast region as much as possible. To achieve this goal, a novel concept called breast probability masks (BPMs) is introduced. A BPM assigns probabilities to each point of a 3D breast scan, telling how likely it is that a particular point belongs to the breast area. During registration, we use BPMs to align the template to the target as accurately as possible inside the breast region and only roughly outside. This simple yet effective strategy significantly reduces the unwanted variance outside the breast region, leading to better statistical shape models in which breast shapes are quite well decoupled from the thorax. The RBSM is thus able to produce a variety of different breast shapes as independently as possible from the shape of the thorax. Our systematic experimental evaluation reveals a generalization ability of 0.17 mm and a specificity of 2.8 mm for the RBSM. Ultimately, our model is seen as a first step towards combining physically motivated deformable models of the breast and statistical approaches in order to enable more realistic surgical outcome simulation.

Tranquil Clouds: Neural Networks for Learning Temporally Coherent Features in Point Clouds

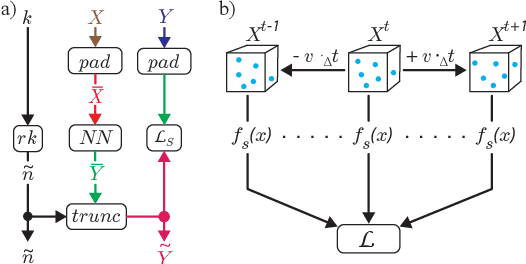
Point clouds, as a form of Lagrangian representation, allow for powerful and flexible applications in a large number of computational disciplines. We propose a novel deep-learning method to learn stable and temporally coherent feature spaces for points clouds that change over time. We identify a set of inherent problems with these approaches: without knowledge of the time dimension, the inferred solutions can exhibit strong flickering, and easy solutions to suppress this flickering can result in undesirable local minima that manifest themselves as halo structures. We propose a novel temporal loss function that takes into account higher time derivatives of the point positions, and encourages mingling, i.e., to prevent the aforementioned halos. We combine these techniques in a super-resolution method with a truncation approach to flexibly adapt the size of the generated positions. We show that our method works for large, deforming point sets from different sources to demonstrate the flexibility of our approach.

Well, how accurate is it? A Study of Deep Learning Methods for Reynolds-Averaged Navier-Stokes Simulations

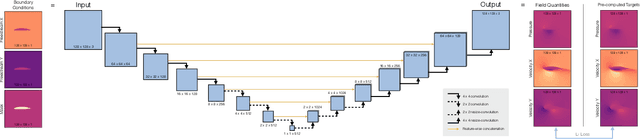
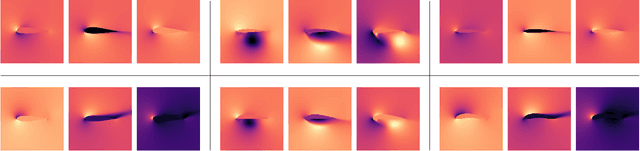
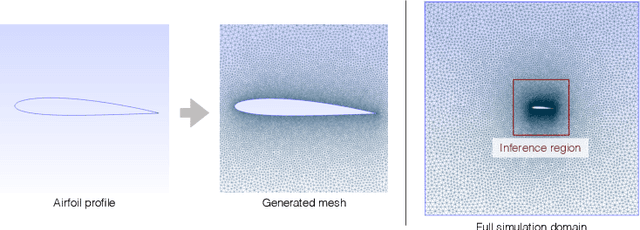
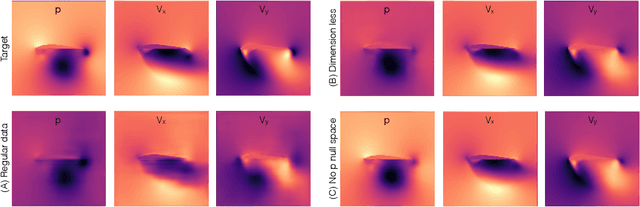
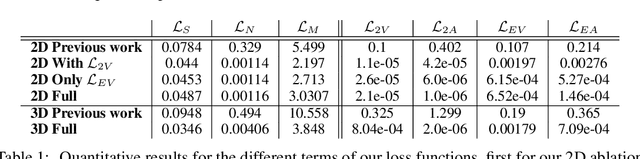
With this study we investigate the accuracy of deep learning models for the inference of Reynolds-Averaged Navier-Stokes solutions. We focus on a modernized U-net architecture, and evaluate a large number of trained neural networks with respect to their accuracy for the calculation of pressure and velocity distributions. In particular, we illustrate how training data size and the number of weights influence the accuracy of the solutions. With our best models we arrive at a mean relative pressure and velocity error of less than 3% across a range of previously unseen airfoil shapes. In addition all source code is publicly available in order to ensure reproducibility and to provide a starting point for researchers interested in deep learning methods for physics problems. While this work focuses on RANS solutions, the neural network architecture and learning setup are very generic, and applicable to a wide range of PDE boundary value problems on Cartesian grids.

Generating Liquid Simulations with Deformation-aware Neural Networks

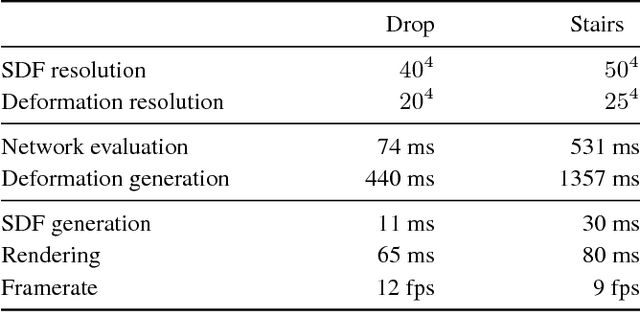
We propose a novel approach for deformation-aware neural networks that learn the weighting and synthesis of dense volumetric deformation fields. Our method specifically targets the space-time representation of physical surfaces from liquid simulations. Liquids exhibit highly complex, non-linear behavior under changing simulation conditions such as different initial conditions. Our algorithm captures these complex phenomena in two stages: a first neural network computes a weighting function for a set of pre-computed deformations, while a second network directly generates a deformation field for refining the surface. Key for successful training runs in this setting is a suitable loss function that encodes the effect of the deformations, and a robust calculation of the corresponding gradients. To demonstrate the effectiveness of our approach, we showcase our method with several complex examples of flowing liquids with topology changes. Our representation makes it possible to rapidly generate the desired implicit surfaces. We have implemented a mobile application to demonstrate that real-time interactions with complex liquid effects are possible with our approach.