Zero-Level-Set Encoder for Neural Distance Fields

Neural shape representation generally refers to representing 3D geometry using neural networks, e.g., to compute a signed distance or occupancy value at a specific spatial position. Previous methods tend to rely on the auto-decoder paradigm, which often requires densely-sampled and accurate signed distances to be known during training and testing, as well as an additional optimization loop during inference. This introduces a lot of computational overhead, in addition to having to compute signed distances analytically, even during testing. In this paper, we present a novel encoder-decoder neural network for embedding 3D shapes in a single forward pass. Our architecture is based on a multi-scale hybrid system incorporating graph-based and voxel-based components, as well as a continuously differentiable decoder. Furthermore, the network is trained to solve the Eikonal equation and only requires knowledge of the zero-level set for training and inference. Additional volumetric samples can be generated on-the-fly, and incorporated in an unsupervised manner. This means that in contrast to most previous work, our network is able to output valid signed distance fields without explicit prior knowledge of non-zero distance values or shape occupancy. In other words, our network computes approximate solutions to the boundary-valued Eikonal equation. It also requires only a single forward pass during inference, instead of the common latent code optimization. We further propose a modification of the loss function in case that surface normals are not well defined, e.g., in the context of non-watertight surface-meshes and non-manifold geometry. We finally demonstrate the efficacy, generalizability and scalability of our method on datasets consisting of deforming 3D shapes, single class encoding and multiclass encoding, showcasing a wide range of possible applications.

Wavelet-based Loss for High-frequency Interface Dynamics

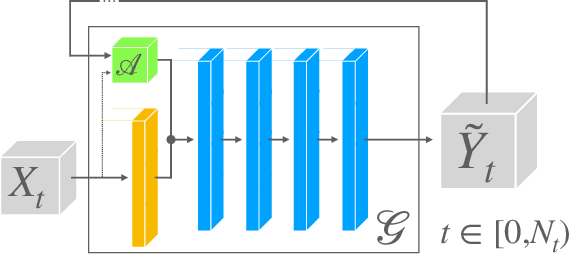
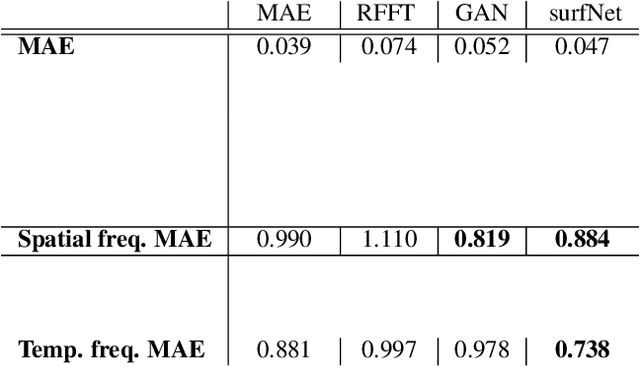
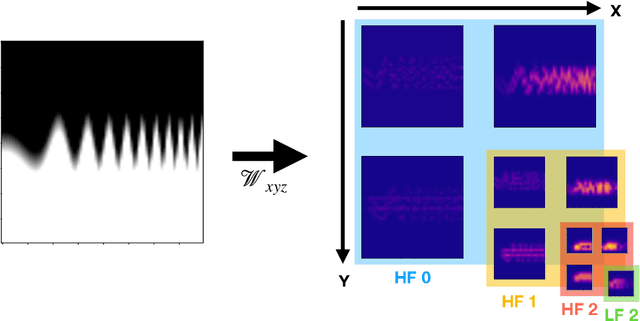
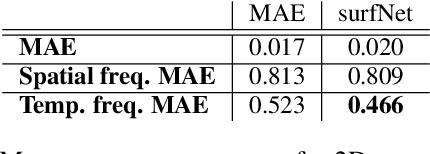
Generating highly detailed, complex data is a long-standing and frequently considered problem in the machine learning field. However, developing detail-aware generators remains an challenging and open problem. Generative adversarial networks are the basis of many state-of-the-art methods. However, they introduce a second network to be trained as a loss function, making the interpretation of the learned functions much more difficult. As an alternative, we present a new method based on a wavelet loss formulation, which remains transparent in terms of what is optimized. The wavelet-based loss function is used to overcome the limitations of conventional distance metrics, such as L1 or L2 distances, when it comes to generate data with high-frequency details. We show that our method can successfully reconstruct high-frequency details in an illustrative synthetic test case. Additionally, we evaluate the performance when applied to more complex surfaces based on physical simulations. Taking a roughly approximated simulation as input, our method infers corresponding spatial details while taking into account how they evolve. We consider this problem in terms of spatial and temporal frequencies, and leverage generative networks trained with our wavelet loss to learn the desired spatio-temporal signal for the surface dynamics. We test the capabilities of our method with a set of synthetic wave function tests and complex 2D and 3D dynamics of elasto-plastic materials.

Accurately Solving Physical Systems with Graph Learning

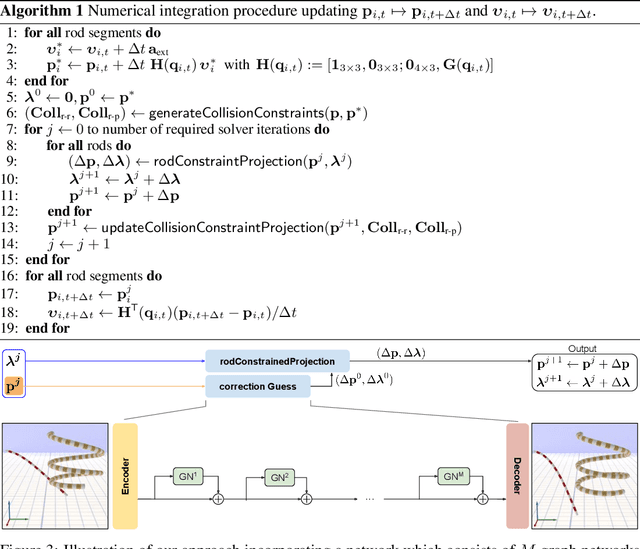
Iterative solvers are widely used to accurately simulate physical systems. These solvers require initial guesses to generate a sequence of improving approximate solutions. In this contribution, we introduce a novel method to accelerate iterative solvers for physical systems with graph networks (GNs) by predicting the initial guesses to reduce the number of iterations. Unlike existing methods that aim to learn physical systems in an end-to-end manner, our approach guarantees long-term stability and therefore leads to more accurate solutions. Furthermore, our method improves the run time performance of traditional iterative solvers. To explore our method we make use of position-based dynamics (PBD) as a common solver for physical systems and evaluate it by simulating the dynamics of elastic rods. Our approach is able to generalize across different initial conditions, discretizations, and realistic material properties. Finally, we demonstrate that our method also performs well when taking discontinuous effects into account such as collisions between individual rods. A video showing dynamic results of our graph learning assisted simulations of elastic rods can be found on the project website available at http://computationalsciences.org/publications/shao-2020-physical-systems-graph-learning.html .