Wavelet-based Loss for High-frequency Interface Dynamics
Paper and Code
Sep 06, 2022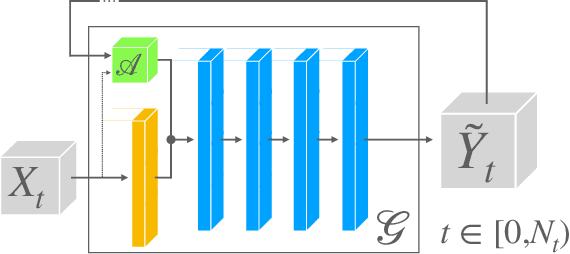
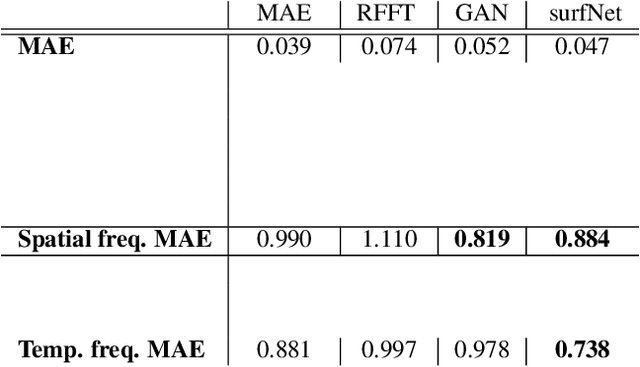
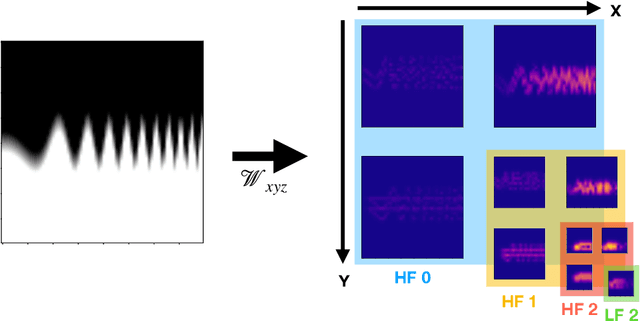
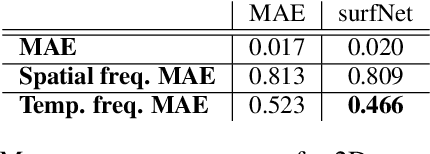
Generating highly detailed, complex data is a long-standing and frequently considered problem in the machine learning field. However, developing detail-aware generators remains an challenging and open problem. Generative adversarial networks are the basis of many state-of-the-art methods. However, they introduce a second network to be trained as a loss function, making the interpretation of the learned functions much more difficult. As an alternative, we present a new method based on a wavelet loss formulation, which remains transparent in terms of what is optimized. The wavelet-based loss function is used to overcome the limitations of conventional distance metrics, such as L1 or L2 distances, when it comes to generate data with high-frequency details. We show that our method can successfully reconstruct high-frequency details in an illustrative synthetic test case. Additionally, we evaluate the performance when applied to more complex surfaces based on physical simulations. Taking a roughly approximated simulation as input, our method infers corresponding spatial details while taking into account how they evolve. We consider this problem in terms of spatial and temporal frequencies, and leverage generative networks trained with our wavelet loss to learn the desired spatio-temporal signal for the surface dynamics. We test the capabilities of our method with a set of synthetic wave function tests and complex 2D and 3D dynamics of elasto-plastic materials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge