Building Retrieval Systems for the ClueWeb22-B Corpus

The ClueWeb22 dataset containing nearly 10 billion documents was released in 2022 to support academic and industry research. The goal of this project was to build retrieval baselines for the English section of the "super head" part (category B) of this dataset. These baselines can then be used by the research community to compare their systems and also to generate data to train/evaluate new retrieval and ranking algorithms. The report covers sparse and dense first stage retrievals as well as neural rerankers that were implemented for this dataset. These systems are available as a service on a Carnegie Mellon University cluster.

Well, how accurate is it? A Study of Deep Learning Methods for Reynolds-Averaged Navier-Stokes Simulations

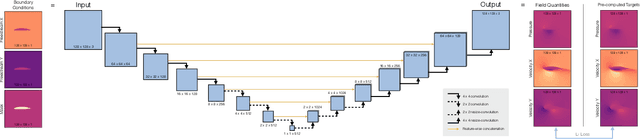
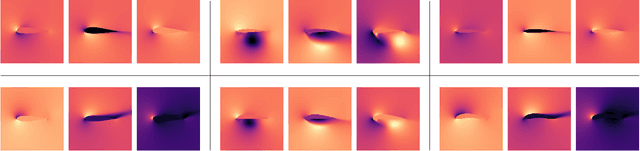
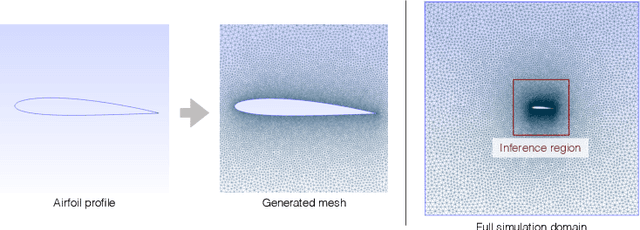
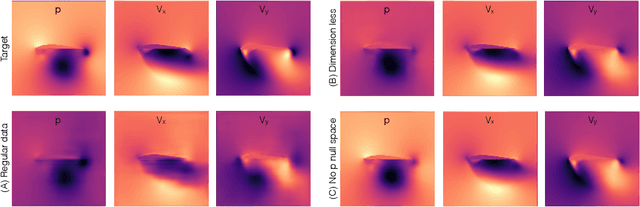
With this study we investigate the accuracy of deep learning models for the inference of Reynolds-Averaged Navier-Stokes solutions. We focus on a modernized U-net architecture, and evaluate a large number of trained neural networks with respect to their accuracy for the calculation of pressure and velocity distributions. In particular, we illustrate how training data size and the number of weights influence the accuracy of the solutions. With our best models we arrive at a mean relative pressure and velocity error of less than 3% across a range of previously unseen airfoil shapes. In addition all source code is publicly available in order to ensure reproducibility and to provide a starting point for researchers interested in deep learning methods for physics problems. While this work focuses on RANS solutions, the neural network architecture and learning setup are very generic, and applicable to a wide range of PDE boundary value problems on Cartesian grids.

Using Chaos in Grey Wolf Optimizer and Application to Prime Factorization

The Grey Wolf Optimizer (GWO) is a swarm intelligence meta-heuristic algorithm inspired by the hunting behaviour and social hierarchy of grey wolves in nature. This paper analyses the use of chaos theory in this algorithm to improve its ability to escape local optima by replacing the key parameters by chaotic variables. The optimal choice of chaotic maps is then used to apply the Chaotic Grey Wolf Optimizer (CGWO) to the problem of factoring a large semi prime into its prime factors. Assuming the number of digits of the factors to be equal, this is a computationally difficult task upon which the RSA-cryptosystem relies. This work proposes the use of a new objective function to solve the problem and uses the CGWO to optimize it and compute the factors. It is shown that this function performs better than its predecessor for large semi primes and CGWO is an efficient algorithm to optimize it.