When Quantization Affects Confidence of Large Language Models?

Recent studies introduced effective compression techniques for Large Language Models (LLMs) via post-training quantization or low-bit weight representation. Although quantized weights offer storage efficiency and allow for faster inference, existing works have indicated that quantization might compromise performance and exacerbate biases in LLMs. This study investigates the confidence and calibration of quantized models, considering factors such as language model type and scale as contributors to quantization loss. Firstly, we reveal that quantization with GPTQ to 4-bit results in a decrease in confidence regarding true labels, with varying impacts observed among different language models. Secondly, we observe fluctuations in the impact on confidence across different scales. Finally, we propose an explanation for quantization loss based on confidence levels, indicating that quantization disproportionately affects samples where the full model exhibited low confidence levels in the first place.

Structure-Preserving Transformers for Sequences of SPD Matrices

In recent years, Transformer-based auto-attention mechanisms have been successfully applied to the analysis of a variety of context-reliant data types, from texts to images and beyond, including data from non-Euclidean geometries. In this paper, we present such a mechanism, designed to classify sequences of Symmetric Positive Definite matrices while preserving their Riemannian geometry throughout the analysis. We apply our method to automatic sleep staging on timeseries of EEG-derived covariance matrices from a standard dataset, obtaining high levels of stage-wise performance.

Maximal Independent Sets for Pooling in Graph Neural Networks

Convolutional Neural Networks (CNNs) have enabled major advances in image classification through convolution and pooling. In particular, image pooling transforms a connected discrete lattice into a reduced lattice with the same connectivity and allows reduction functions to consider all pixels in an image. However, there is no pooling that satisfies these properties for graphs. In fact, traditional graph pooling methods suffer from at least one of the following drawbacks: Graph disconnection or overconnection, low decimation ratio, and deletion of large parts of graphs. In this paper, we present three pooling methods based on the notion of maximal independent sets that avoid these pitfalls. Our experimental results confirm the relevance of maximal independent set constraints for graph pooling.

Maximal Independent Vertex Set applied to Graph Pooling

Convolutional neural networks (CNN) have enabled major advances in image classification through convolution and pooling. In particular, image pooling transforms a connected discrete grid into a reduced grid with the same connectivity and allows reduction functions to take into account all the pixels of an image. However, a pooling satisfying such properties does not exist for graphs. Indeed, some methods are based on a vertex selection step which induces an important loss of information. Other methods learn a fuzzy clustering of vertex sets which induces almost complete reduced graphs. We propose to overcome both problems using a new pooling method, named MIVSPool. This method is based on a selection of vertices called surviving vertices using a Maximal Independent Vertex Set (MIVS) and an assignment of the remaining vertices to the survivors. Consequently, our method does not discard any vertex information nor artificially increase the density of the graph. Experimental results show an increase in accuracy for graph classification on various standard datasets.

A new Sinkhorn algorithm with Deletion and Insertion operations

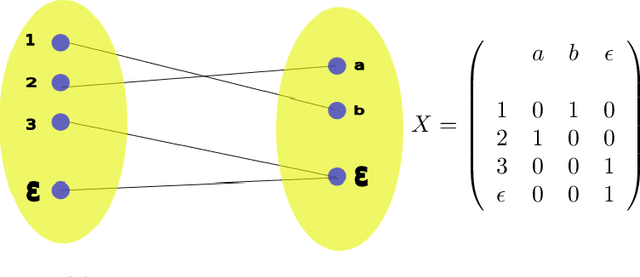
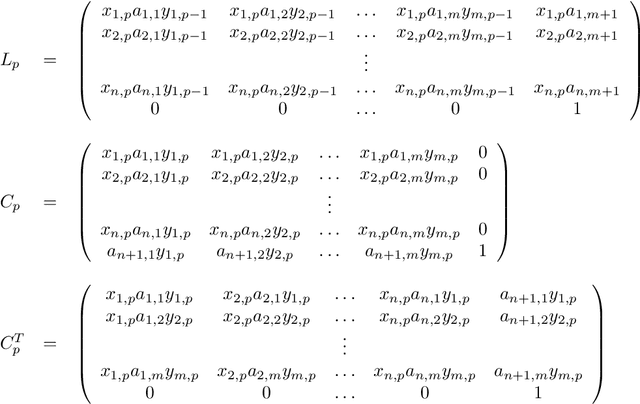
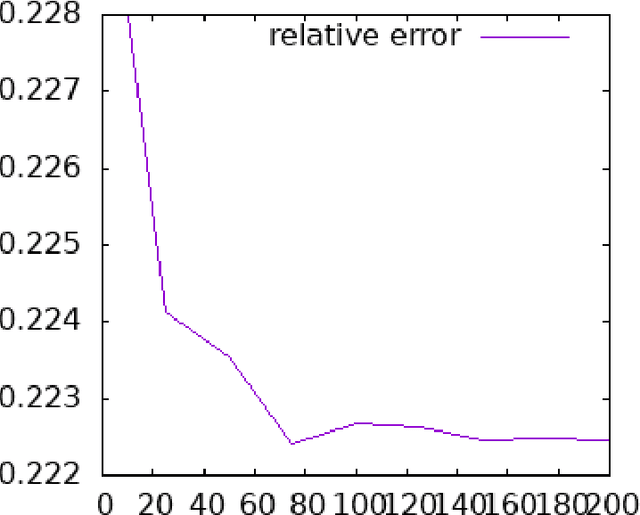
This technical report is devoted to the continuous estimation of an epsilon-assignment. Roughly speaking, an epsilon assignment between two sets V1 and V2 may be understood as a bijective mapping between a sub part of V1 and a sub part of V2 . The remaining elements of V1 (not included in this mapping) are mapped onto an epsilon pseudo element of V2 . We say that such elements are deleted. Conversely, the remaining elements of V2 correspond to the image of the epsilon pseudo element of V1. We say that these elements are inserted. As a result our method provides a result similar to the one of the Sinkhorn algorithm with the additional ability to reject some elements which are either inserted or deleted. It thus naturally handles sets V1 and V2 of different sizes and decides mappings/insertions/deletions in a unified way. Our algorithms are iterative and differentiable and may thus be easily inserted within a backpropagation based learning framework such as artificial neural networks.

Improved local search for graph edit distance

Graph Edit Distance (GED) measures the dissimilarity between two graphs as the minimal cost of a sequence of elementary operations transforming one graph into another. This measure is fundamental in many areas such as structural pattern recognition or classification. However, exactly computing GED is NP-hard. Among different classes of heuristic algorithms that were proposed to compute approximate solutions, local search based algorithms provide the tightest upper bounds for GED. In this paper, we present K-REFINE and RANDPOST. K-REFINE generalizes and improves an existing local search algorithm and performs particularly well on small graphs. RANDPOST is a general warm start framework that stochastically generates promising initial solutions to be used by any local search based GED algorithm. It is particularly efficient on large graphs. An extensive empirical evaluation demonstrates that both K-REFINE and RANDPOST perform excellently in practice.

Generalized Median Graph via Iterative Alternate Minimizations

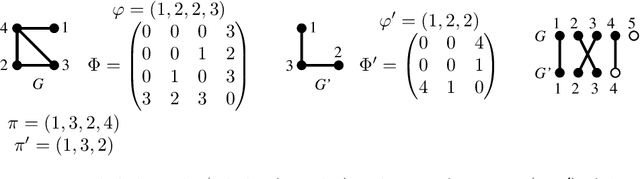
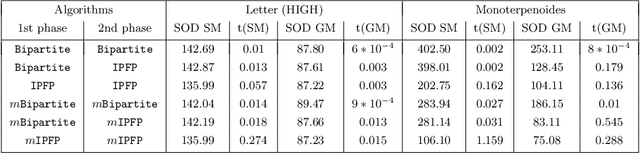
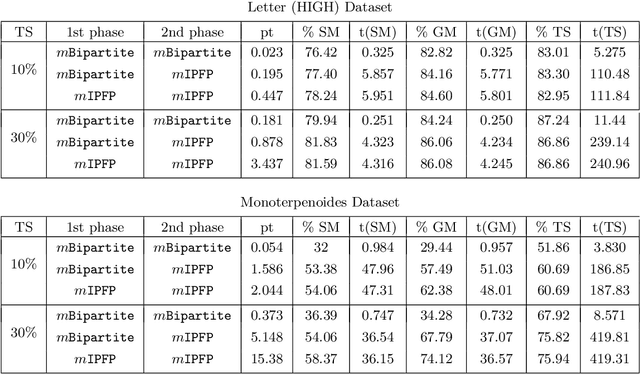
Computing a graph prototype may constitute a core element for clustering or classification tasks. However, its computation is an NP-Hard problem, even for simple classes of graphs. In this paper, we propose an efficient approach based on block coordinate descent to compute a generalized median graph from a set of graphs. This approach relies on a clear definition of the optimization process and handles labeling on both edges and nodes. This iterative process optimizes the edit operations to perform on a graph alternatively on nodes and edges. Several experiments on different datasets show the efficiency of our approach.

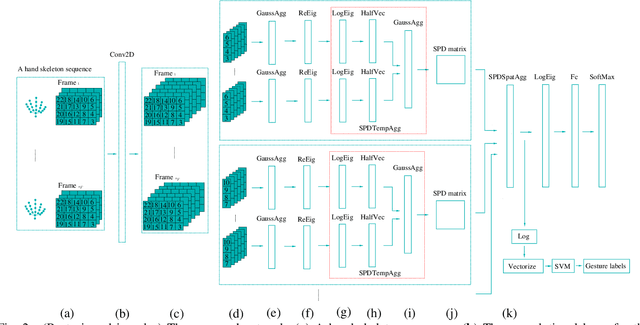
Skeleton-Based Hand Gesture Recognition by Learning SPD Matrices with Neural Networks

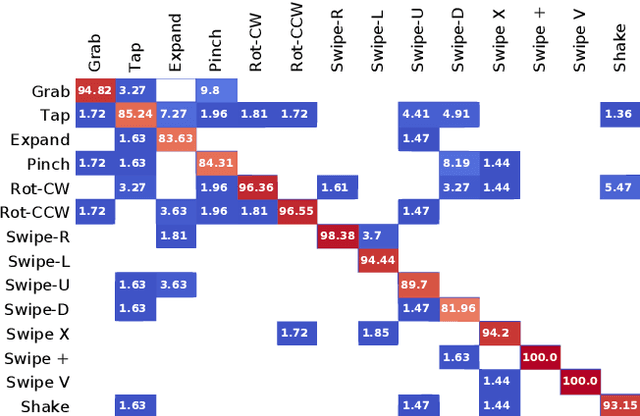
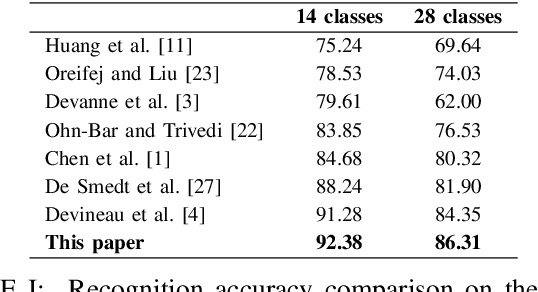
In this paper, we propose a new hand gesture recognition method based on skeletal data by learning SPD matrices with neural networks. We model the hand skeleton as a graph and introduce a neural network for SPD matrix learning, taking as input the 3D coordinates of hand joints. The proposed network is based on two newly designed layers that transform a set of SPD matrices into a SPD matrix. For gesture recognition, we train a linear SVM classifier using features extracted from our network. Experimental results on a challenging dataset (Dynamic Hand Gesture dataset from the SHREC 2017 3D Shape Retrieval Contest) show that the proposed method outperforms state-of-the-art methods.

A neural network based on SPD manifold learning for skeleton-based hand gesture recognition

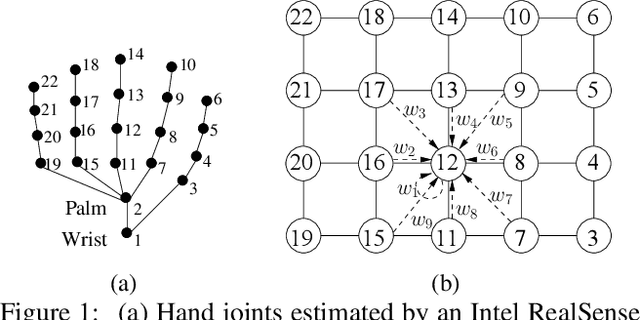
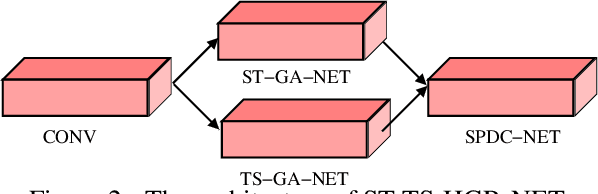
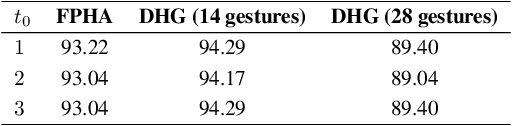
This paper proposes a new neural network based on SPD manifold learning for skeleton-based hand gesture recognition. Given the stream of hand's joint positions, our approach combines two aggregation processes on respectively spatial and temporal domains. The pipeline of our network architecture consists in three main stages. The first stage is based on a convolutional layer to increase the discriminative power of learned features. The second stage relies on different architectures for spatial and temporal Gaussian aggregation of joint features. The third stage learns a final SPD matrix from skeletal data. A new type of layer is proposed for the third stage, based on a variant of stochastic gradient descent on Stiefel manifolds. The proposed network is validated on two challenging datasets and shows state-of-the-art accuracies on both datasets.

Combinatorial pyramids and discrete geometry for energy-minimizing segmentation

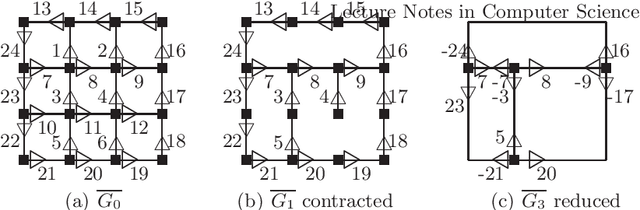
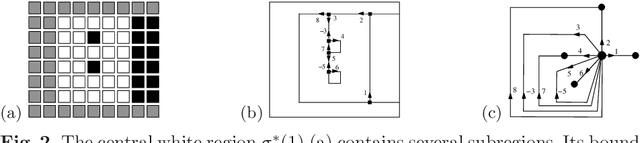
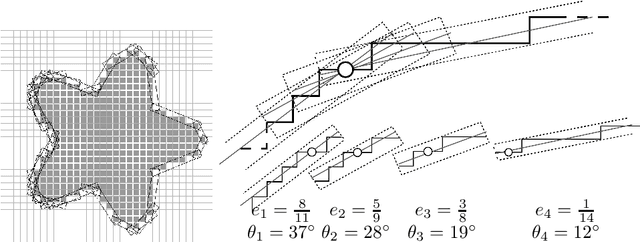
This paper defines the basis of a new hierarchical framework for segmentation algorithms based on energy minimization schemes. This new framework is based on two formal tools. First, a combinatorial pyramid encode efficiently a hierarchy of partitions. Secondly, discrete geometric estimators measure precisely some important geometric parameters of the regions. These measures combined with photometrical and topological features of the partition allows to design energy terms based on discrete measures. Our segmentation framework exploits these energies to build a pyramid of image partitions with a minimization scheme. Some experiments illustrating our framework are shown and discussed.