The Minimum Edit Arborescence Problem and Its Use in Compressing Graph Collections

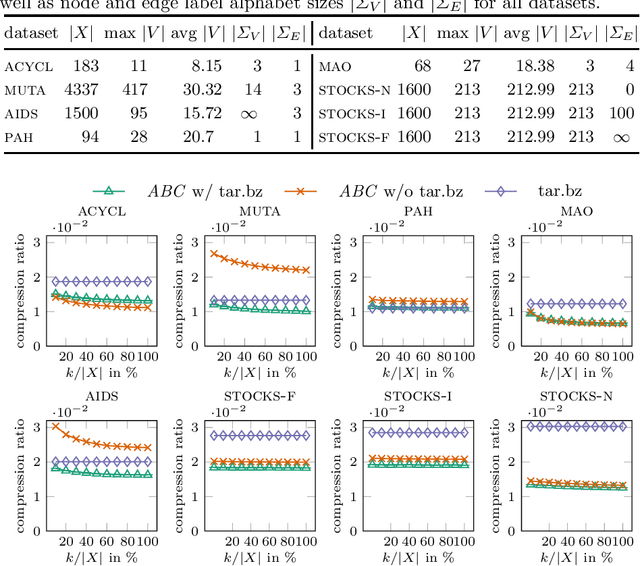
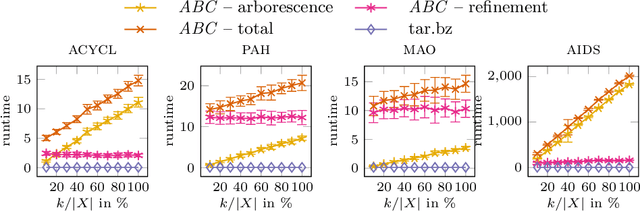
The inference of minimum spanning arborescences within a set of objects is a general problem which translates into numerous application-specific unsupervised learning tasks. We introduce a unified and generic structure called edit arborescence that relies on edit paths between data in a collection, as well as the Min Edit Arborescence Problem, which asks for an edit arborescence that minimizes the sum of costs of its inner edit paths. Through the use of suitable cost functions, this generic framework allows to model a variety of problems. In particular, we show that by introducing encoding size preserving edit costs, it can be used as an efficient method for compressing collections of labeled graphs. Experiments on various graph datasets, with comparisons to standard compression tools, show the potential of our method.

Improved local search for graph edit distance

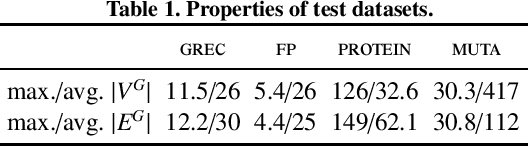
Graph Edit Distance (GED) measures the dissimilarity between two graphs as the minimal cost of a sequence of elementary operations transforming one graph into another. This measure is fundamental in many areas such as structural pattern recognition or classification. However, exactly computing GED is NP-hard. Among different classes of heuristic algorithms that were proposed to compute approximate solutions, local search based algorithms provide the tightest upper bounds for GED. In this paper, we present K-REFINE and RANDPOST. K-REFINE generalizes and improves an existing local search algorithm and performs particularly well on small graphs. RANDPOST is a general warm start framework that stochastically generates promising initial solutions to be used by any local search based GED algorithm. It is particularly efficient on large graphs. An extensive empirical evaluation demonstrates that both K-REFINE and RANDPOST perform excellently in practice.

Generalized Median Graph via Iterative Alternate Minimizations

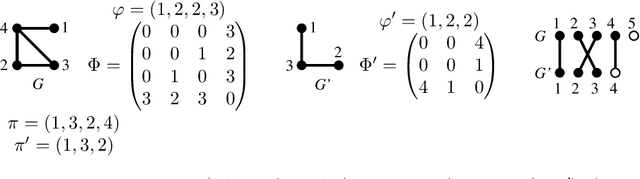
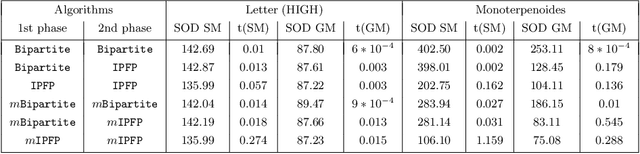
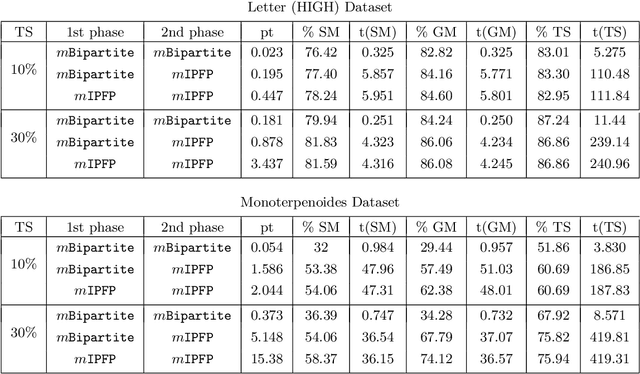
Computing a graph prototype may constitute a core element for clustering or classification tasks. However, its computation is an NP-Hard problem, even for simple classes of graphs. In this paper, we propose an efficient approach based on block coordinate descent to compute a generalized median graph from a set of graphs. This approach relies on a clear definition of the optimization process and handles labeling on both edges and nodes. This iterative process optimizes the edit operations to perform on a graph alternatively on nodes and edges. Several experiments on different datasets show the efficiency of our approach.