A new Sinkhorn algorithm with Deletion and Insertion operations

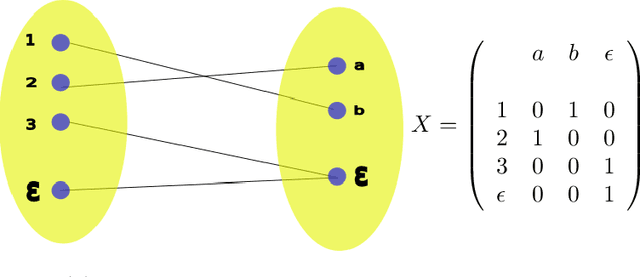
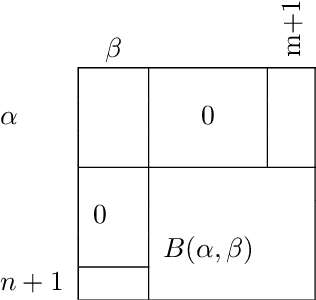
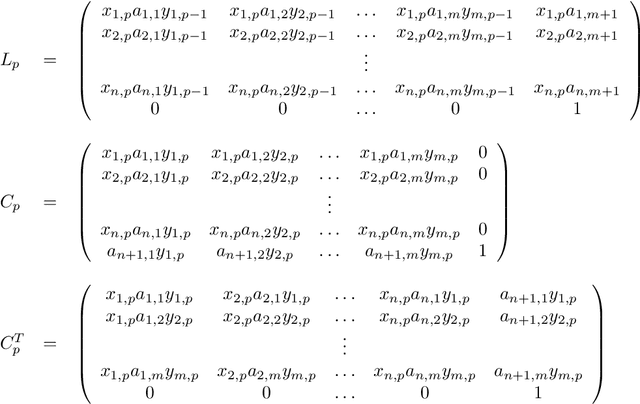
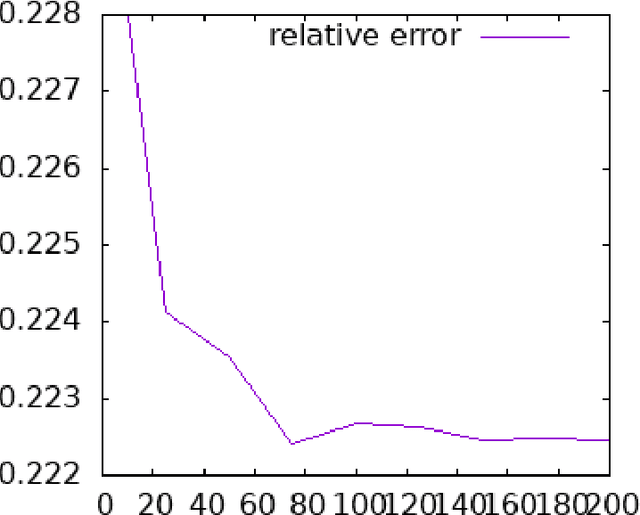
This technical report is devoted to the continuous estimation of an epsilon-assignment. Roughly speaking, an epsilon assignment between two sets V1 and V2 may be understood as a bijective mapping between a sub part of V1 and a sub part of V2 . The remaining elements of V1 (not included in this mapping) are mapped onto an epsilon pseudo element of V2 . We say that such elements are deleted. Conversely, the remaining elements of V2 correspond to the image of the epsilon pseudo element of V1. We say that these elements are inserted. As a result our method provides a result similar to the one of the Sinkhorn algorithm with the additional ability to reject some elements which are either inserted or deleted. It thus naturally handles sets V1 and V2 of different sizes and decides mappings/insertions/deletions in a unified way. Our algorithms are iterative and differentiable and may thus be easily inserted within a backpropagation based learning framework such as artificial neural networks.

The Minimum Edit Arborescence Problem and Its Use in Compressing Graph Collections

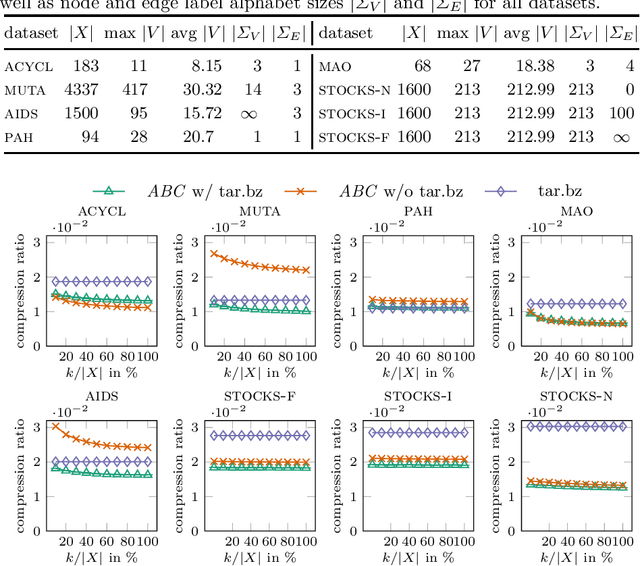
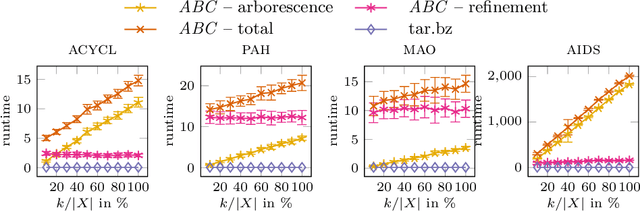
The inference of minimum spanning arborescences within a set of objects is a general problem which translates into numerous application-specific unsupervised learning tasks. We introduce a unified and generic structure called edit arborescence that relies on edit paths between data in a collection, as well as the Min Edit Arborescence Problem, which asks for an edit arborescence that minimizes the sum of costs of its inner edit paths. Through the use of suitable cost functions, this generic framework allows to model a variety of problems. In particular, we show that by introducing encoding size preserving edit costs, it can be used as an efficient method for compressing collections of labeled graphs. Experiments on various graph datasets, with comparisons to standard compression tools, show the potential of our method.

Improved local search for graph edit distance

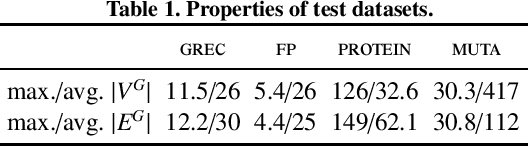
Graph Edit Distance (GED) measures the dissimilarity between two graphs as the minimal cost of a sequence of elementary operations transforming one graph into another. This measure is fundamental in many areas such as structural pattern recognition or classification. However, exactly computing GED is NP-hard. Among different classes of heuristic algorithms that were proposed to compute approximate solutions, local search based algorithms provide the tightest upper bounds for GED. In this paper, we present K-REFINE and RANDPOST. K-REFINE generalizes and improves an existing local search algorithm and performs particularly well on small graphs. RANDPOST is a general warm start framework that stochastically generates promising initial solutions to be used by any local search based GED algorithm. It is particularly efficient on large graphs. An extensive empirical evaluation demonstrates that both K-REFINE and RANDPOST perform excellently in practice.

Skeleton-Based Hand Gesture Recognition by Learning SPD Matrices with Neural Networks

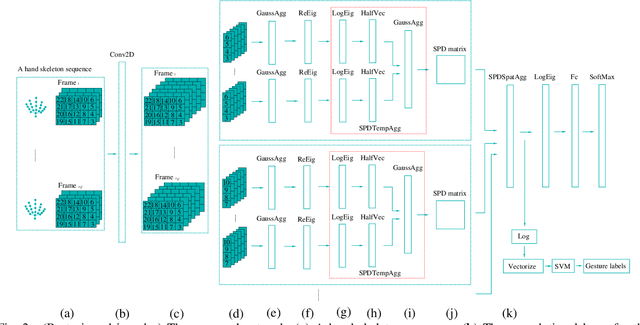
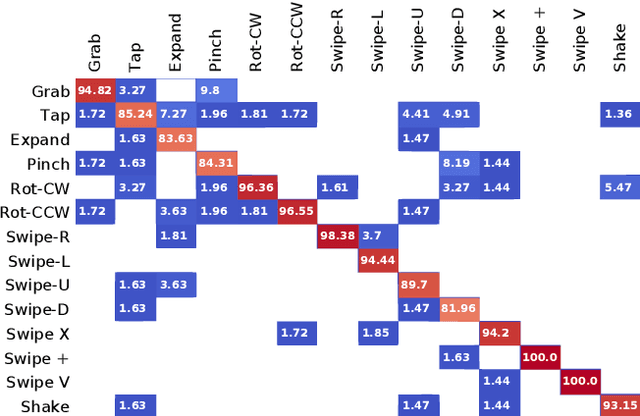
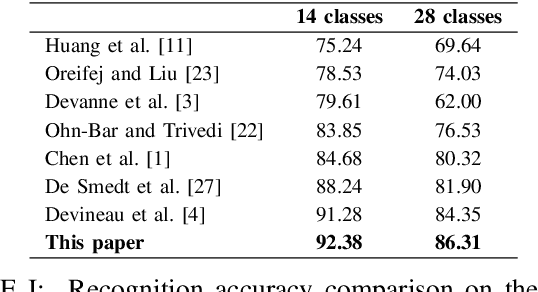
In this paper, we propose a new hand gesture recognition method based on skeletal data by learning SPD matrices with neural networks. We model the hand skeleton as a graph and introduce a neural network for SPD matrix learning, taking as input the 3D coordinates of hand joints. The proposed network is based on two newly designed layers that transform a set of SPD matrices into a SPD matrix. For gesture recognition, we train a linear SVM classifier using features extracted from our network. Experimental results on a challenging dataset (Dynamic Hand Gesture dataset from the SHREC 2017 3D Shape Retrieval Contest) show that the proposed method outperforms state-of-the-art methods.

A neural network based on SPD manifold learning for skeleton-based hand gesture recognition

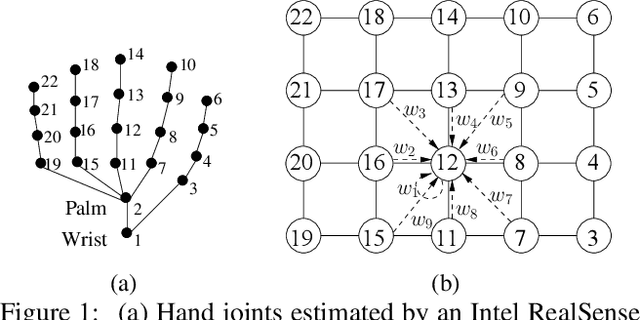
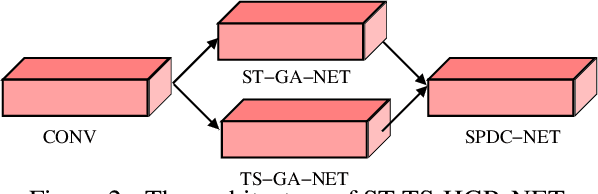
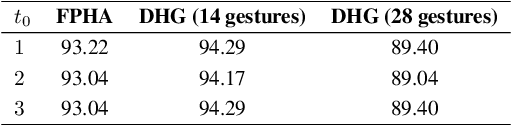
This paper proposes a new neural network based on SPD manifold learning for skeleton-based hand gesture recognition. Given the stream of hand's joint positions, our approach combines two aggregation processes on respectively spatial and temporal domains. The pipeline of our network architecture consists in three main stages. The first stage is based on a convolutional layer to increase the discriminative power of learned features. The second stage relies on different architectures for spatial and temporal Gaussian aggregation of joint features. The third stage learns a final SPD matrix from skeletal data. A new type of layer is proposed for the third stage, based on a variant of stochastic gradient descent on Stiefel manifolds. The proposed network is validated on two challenging datasets and shows state-of-the-art accuracies on both datasets.