Matrix Manifold Neural Networks++

Deep neural networks (DNNs) on Riemannian manifolds have garnered increasing interest in various applied areas. For instance, DNNs on spherical and hyperbolic manifolds have been designed to solve a wide range of computer vision and nature language processing tasks. One of the key factors that contribute to the success of these networks is that spherical and hyperbolic manifolds have the rich algebraic structures of gyrogroups and gyrovector spaces. This enables principled and effective generalizations of the most successful DNNs to these manifolds. Recently, some works have shown that many concepts in the theory of gyrogroups and gyrovector spaces can also be generalized to matrix manifolds such as Symmetric Positive Definite (SPD) and Grassmann manifolds. As a result, some building blocks for SPD and Grassmann neural networks, e.g., isometric models and multinomial logistic regression (MLR) can be derived in a way that is fully analogous to their spherical and hyperbolic counterparts. Building upon these works, we design fully-connected (FC) and convolutional layers for SPD neural networks. We also develop MLR on Symmetric Positive Semi-definite (SPSD) manifolds, and propose a method for performing backpropagation with the Grassmann logarithmic map in the projector perspective. We demonstrate the effectiveness of the proposed approach in the human action recognition and node classification tasks.

Building Neural Networks on Matrix Manifolds: A Gyrovector Space Approach

Matrix manifolds, such as manifolds of Symmetric Positive Definite (SPD) matrices and Grassmann manifolds, appear in many applications. Recently, by applying the theory of gyrogroups and gyrovector spaces that is a powerful framework for studying hyperbolic geometry, some works have attempted to build principled generalizations of Euclidean neural networks on matrix manifolds. However, due to the lack of many concepts in gyrovector spaces for the considered manifolds, e.g., the inner product and gyroangles, techniques and mathematical tools provided by these works are still limited compared to those developed for studying hyperbolic geometry. In this paper, we generalize some notions in gyrovector spaces for SPD and Grassmann manifolds, and propose new models and layers for building neural networks on these manifolds. We show the effectiveness of our approach in two applications, i.e., human action recognition and knowledge graph completion.

GeomNet: A Neural Network Based on Riemannian Geometries of SPD Matrix Space and Cholesky Space for 3D Skeleton-Based Interaction Recognition

In this paper, we propose a novel method for representation and classification of two-person interactions from 3D skeleton sequences. The key idea of our approach is to use Gaussian distributions to capture statistics on R n and those on the space of symmetric positive definite (SPD) matrices. The main challenge is how to parametrize those distributions. Towards this end, we develop methods for embedding Gaussian distributions in matrix groups based on the theory of Lie groups and Riemannian symmetric spaces. Our method relies on the Riemannian geometry of the underlying manifolds and has the advantage of encoding high-order statistics from 3D joint positions. We show that the proposed method achieves competitive results in two-person interaction recognition on three benchmarks for 3D human activity understanding.

A neural network based on SPD manifold learning for skeleton-based hand gesture recognition

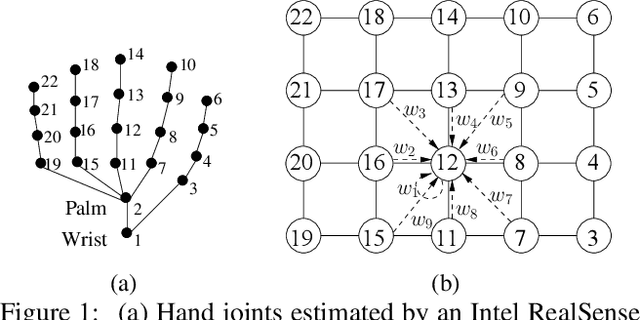
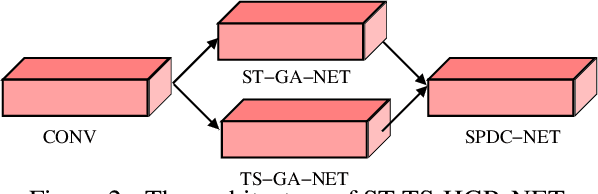
This paper proposes a new neural network based on SPD manifold learning for skeleton-based hand gesture recognition. Given the stream of hand's joint positions, our approach combines two aggregation processes on respectively spatial and temporal domains. The pipeline of our network architecture consists in three main stages. The first stage is based on a convolutional layer to increase the discriminative power of learned features. The second stage relies on different architectures for spatial and temporal Gaussian aggregation of joint features. The third stage learns a final SPD matrix from skeletal data. A new type of layer is proposed for the third stage, based on a variant of stochastic gradient descent on Stiefel manifolds. The proposed network is validated on two challenging datasets and shows state-of-the-art accuracies on both datasets.