Maximal Independent Sets for Pooling in Graph Neural Networks

Convolutional Neural Networks (CNNs) have enabled major advances in image classification through convolution and pooling. In particular, image pooling transforms a connected discrete lattice into a reduced lattice with the same connectivity and allows reduction functions to consider all pixels in an image. However, there is no pooling that satisfies these properties for graphs. In fact, traditional graph pooling methods suffer from at least one of the following drawbacks: Graph disconnection or overconnection, low decimation ratio, and deletion of large parts of graphs. In this paper, we present three pooling methods based on the notion of maximal independent sets that avoid these pitfalls. Our experimental results confirm the relevance of maximal independent set constraints for graph pooling.

Maximal Independent Vertex Set applied to Graph Pooling

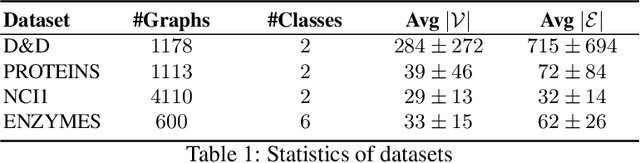
Convolutional neural networks (CNN) have enabled major advances in image classification through convolution and pooling. In particular, image pooling transforms a connected discrete grid into a reduced grid with the same connectivity and allows reduction functions to take into account all the pixels of an image. However, a pooling satisfying such properties does not exist for graphs. Indeed, some methods are based on a vertex selection step which induces an important loss of information. Other methods learn a fuzzy clustering of vertex sets which induces almost complete reduced graphs. We propose to overcome both problems using a new pooling method, named MIVSPool. This method is based on a selection of vertices called surviving vertices using a Maximal Independent Vertex Set (MIVS) and an assignment of the remaining vertices to the survivors. Consequently, our method does not discard any vertex information nor artificially increase the density of the graph. Experimental results show an increase in accuracy for graph classification on various standard datasets.

A new Sinkhorn algorithm with Deletion and Insertion operations

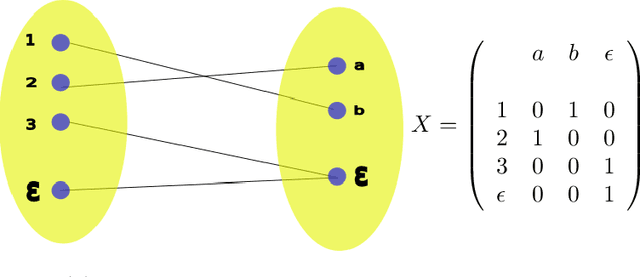
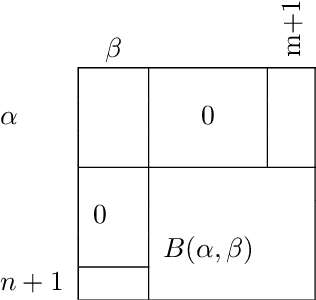
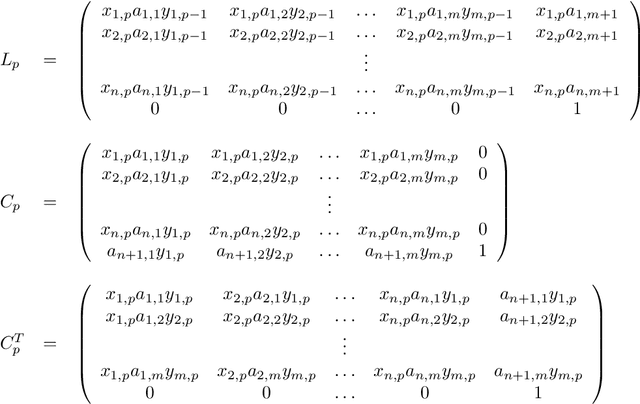
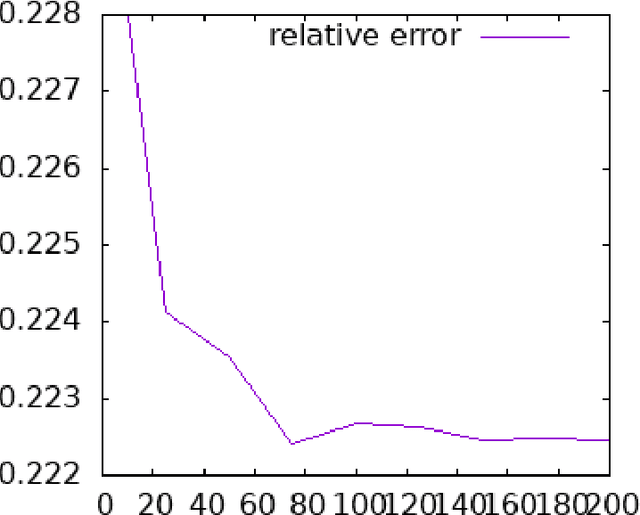
This technical report is devoted to the continuous estimation of an epsilon-assignment. Roughly speaking, an epsilon assignment between two sets V1 and V2 may be understood as a bijective mapping between a sub part of V1 and a sub part of V2 . The remaining elements of V1 (not included in this mapping) are mapped onto an epsilon pseudo element of V2 . We say that such elements are deleted. Conversely, the remaining elements of V2 correspond to the image of the epsilon pseudo element of V1. We say that these elements are inserted. As a result our method provides a result similar to the one of the Sinkhorn algorithm with the additional ability to reject some elements which are either inserted or deleted. It thus naturally handles sets V1 and V2 of different sizes and decides mappings/insertions/deletions in a unified way. Our algorithms are iterative and differentiable and may thus be easily inserted within a backpropagation based learning framework such as artificial neural networks.

Breaking the Limits of Message Passing Graph Neural Networks

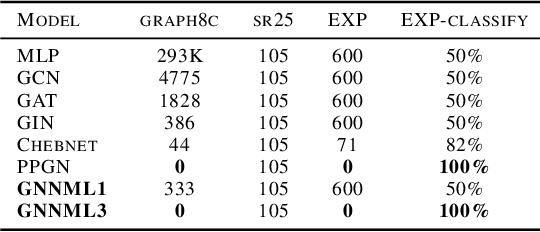
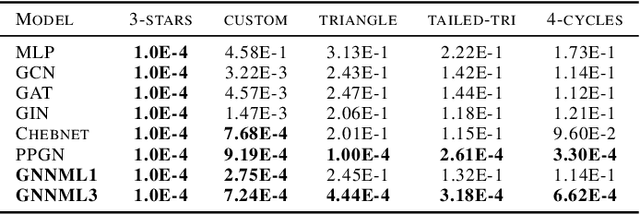
Since the Message Passing (Graph) Neural Networks (MPNNs) have a linear complexity with respect to the number of nodes when applied to sparse graphs, they have been widely implemented and still raise a lot of interest even though their theoretical expressive power is limited to the first order Weisfeiler-Lehman test (1-WL). In this paper, we show that if the graph convolution supports are designed in spectral-domain by a non-linear custom function of eigenvalues and masked with an arbitrary large receptive field, the MPNN is theoretically more powerful than the 1-WL test and experimentally as powerful as a 3-WL existing models, while remaining spatially localized. Moreover, by designing custom filter functions, outputs can have various frequency components that allow the convolution process to learn different relationships between a given input graph signal and its associated properties. So far, the best 3-WL equivalent graph neural networks have a computational complexity in $\mathcal{O}(n^3)$ with memory usage in $\mathcal{O}(n^2)$, consider non-local update mechanism and do not provide the spectral richness of output profile. The proposed method overcomes all these aforementioned problems and reaches state-of-the-art results in many downstream tasks.

Generalized Median Graph via Iterative Alternate Minimizations

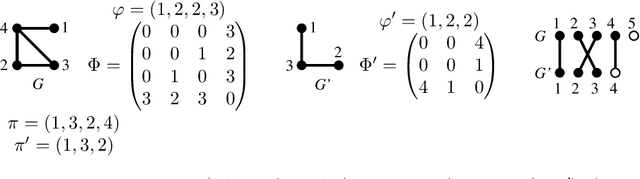
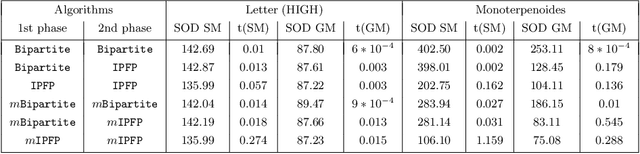
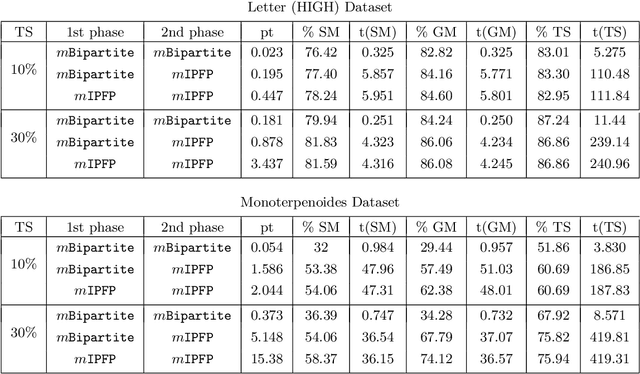
Computing a graph prototype may constitute a core element for clustering or classification tasks. However, its computation is an NP-Hard problem, even for simple classes of graphs. In this paper, we propose an efficient approach based on block coordinate descent to compute a generalized median graph from a set of graphs. This approach relies on a clear definition of the optimization process and handles labeling on both edges and nodes. This iterative process optimizes the edit operations to perform on a graph alternatively on nodes and edges. Several experiments on different datasets show the efficiency of our approach.