Finding path and cycle counting formulae in graphs with Deep Reinforcement Learning

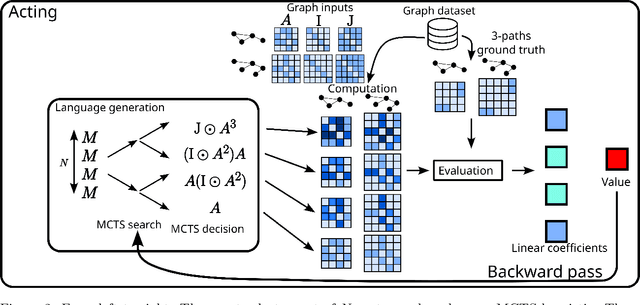
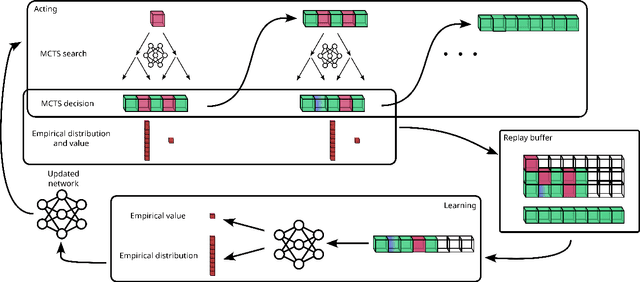
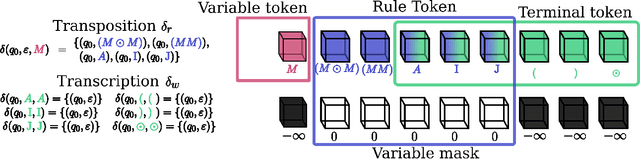
This paper presents Grammar Reinforcement Learning (GRL), a reinforcement learning algorithm that uses Monte Carlo Tree Search (MCTS) and a transformer architecture that models a Pushdown Automaton (PDA) within a context-free grammar (CFG) framework. Taking as use case the problem of efficiently counting paths and cycles in graphs, a key challenge in network analysis, computer science, biology, and social sciences, GRL discovers new matrix-based formulas for path/cycle counting that improve computational efficiency by factors of two to six w.r.t state-of-the-art approaches. Our contributions include: (i) a framework for generating gramformers that operate within a CFG, (ii) the development of GRL for optimizing formulas within grammatical structures, and (iii) the discovery of novel formulas for graph substructure counting, leading to significant computational improvements.

Technical report: Graph Neural Networks go Grammatical

This paper proposes a new GNN design strategy. This strategy relies on Context-Free Grammars (CFG) generating the matrix language MATLANG. It enables us to ensure both WL-expressive power, substructure counting abilities and spectral properties. Applying our strategy, we design Grammatical Graph Neural Network G$ ^2$N$^2$, a provably 3-WL GNN able to count at edge-level cycles of length up to 6 and able to reach band-pass filters. A large number of experiments covering these properties corroborate the presented theoretical results.

Breaking the Limits of Message Passing Graph Neural Networks

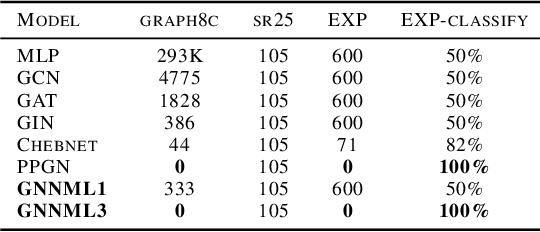
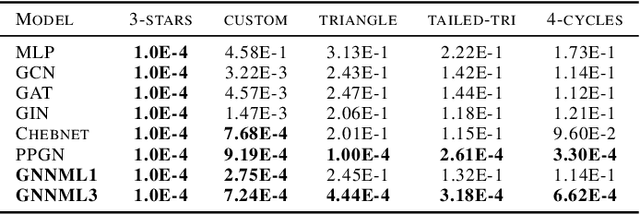
Since the Message Passing (Graph) Neural Networks (MPNNs) have a linear complexity with respect to the number of nodes when applied to sparse graphs, they have been widely implemented and still raise a lot of interest even though their theoretical expressive power is limited to the first order Weisfeiler-Lehman test (1-WL). In this paper, we show that if the graph convolution supports are designed in spectral-domain by a non-linear custom function of eigenvalues and masked with an arbitrary large receptive field, the MPNN is theoretically more powerful than the 1-WL test and experimentally as powerful as a 3-WL existing models, while remaining spatially localized. Moreover, by designing custom filter functions, outputs can have various frequency components that allow the convolution process to learn different relationships between a given input graph signal and its associated properties. So far, the best 3-WL equivalent graph neural networks have a computational complexity in $\mathcal{O}(n^3)$ with memory usage in $\mathcal{O}(n^2)$, consider non-local update mechanism and do not provide the spectral richness of output profile. The proposed method overcomes all these aforementioned problems and reaches state-of-the-art results in many downstream tasks.

Graph edit distance : a new binary linear programming formulation

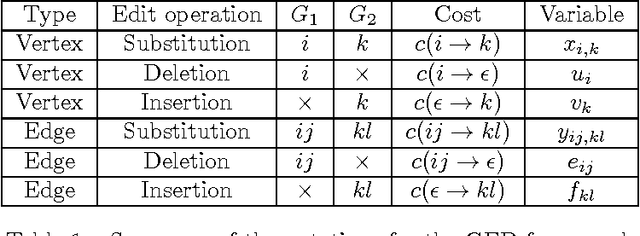
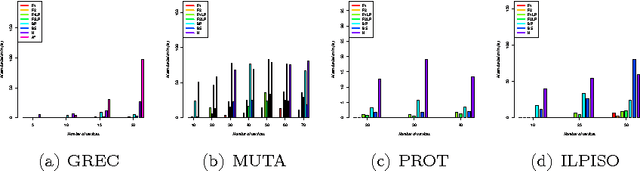
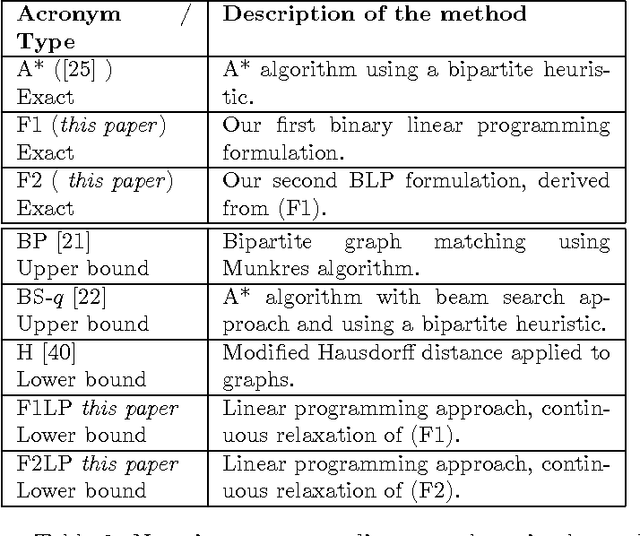
Graph edit distance (GED) is a powerful and flexible graph matching paradigm that can be used to address different tasks in structural pattern recognition, machine learning, and data mining. In this paper, some new binary linear programming formulations for computing the exact GED between two graphs are proposed. A major strength of the formulations lies in their genericity since the GED can be computed between directed or undirected fully attributed graphs (i.e. with attributes on both vertices and edges). Moreover, a relaxation of the domain constraints in the formulations provides efficient lower bound approximations of the GED. A complete experimental study comparing the proposed formulations with 4 state-of-the-art algorithms for exact and approximate graph edit distances is provided. By considering both the quality of the proposed solution and the efficiency of the algorithms as performance criteria, the results show that none of the compared methods dominates the others in the Pareto sense. As a consequence, faced to a given real-world problem, a trade-off between quality and efficiency has to be chosen w.r.t. the application constraints. In this context, this paper provides a guide that can be used to choose the appropriate method.