Deformable Model with a Complexity Independent from Image Resolution

We present a parametric deformable model which recovers image components with a complexity independent from the resolution of input images. The proposed model also automatically changes its topology and remains fully compatible with the general framework of deformable models. More precisely, the image space is equipped with a metric that expands salient image details according to their strength and their curvature. During the whole evolution of the model, the sampling of the contour is kept regular with respect to this metric. By this way, the vertex density is reduced along most parts of the curve while a high quality of shape representation is preserved. The complexity of the deformable model is thus improved and is no longer influenced by feature-preserving changes in the resolution of input images. Building the metric requires a prior estimation of contour curvature. It is obtained using a robust estimator which investigates the local variations in the orientation of image gradient. Experimental results on both computer generated and biomedical images are presented to illustrate the advantages of our approach.

Combinatorial pyramids and discrete geometry for energy-minimizing segmentation

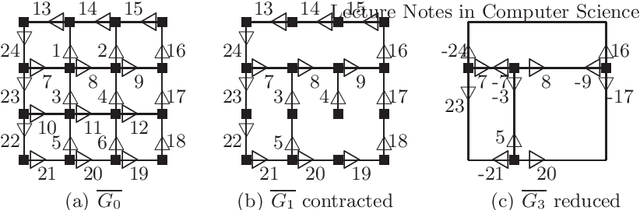
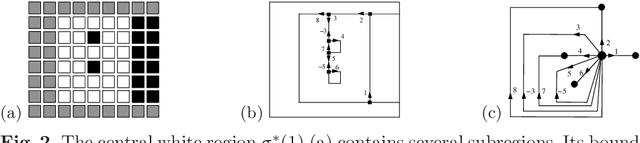
This paper defines the basis of a new hierarchical framework for segmentation algorithms based on energy minimization schemes. This new framework is based on two formal tools. First, a combinatorial pyramid encode efficiently a hierarchy of partitions. Secondly, discrete geometric estimators measure precisely some important geometric parameters of the regions. These measures combined with photometrical and topological features of the partition allows to design energy terms based on discrete measures. Our segmentation framework exploits these energies to build a pyramid of image partitions with a minimization scheme. Some experiments illustrating our framework are shown and discussed.

Coding cells of digital spaces: a framework to write generic digital topology algorithms

This paper proposes a concise coding of the cells of n-dimensional finite regular grids. It induces a simple, generic and efficient framework for implementing classical digital topology data structures and algorithms. Discrete subsets of multidimensional images (e.g. regions, digital surfaces, cubical cell complexes) have then a common and compact representation. Moreover, algorithms have a straightforward and efficient implementation, which is independent from the dimension or sizes of digital images. We illustrate that point with generic hypersurface boundary extraction algorithms by scanning or tracking. This framework has been implemented and basic operations as well as the presented applications have been benchmarked.

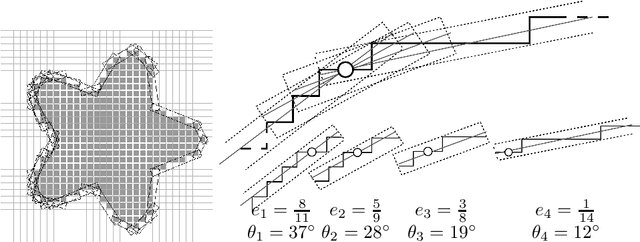
Maximal digital straight segments and convergence of discrete geometric estimators

Discrete geometric estimators approach geometric quantities on digitized shapes without any knowledge of the continuous shape. A classical yet difficult problem is to show that an estimator asymptotically converges toward the true geometric quantity as the resolution increases. We study here the convergence of local estimators based on Digital Straight Segment (DSS) recognition. It is closely linked to the asymptotic growth of maximal DSS, for which we show bounds both about their number and sizes. These results not only give better insights about digitized curves but indicate that curvature estimators based on local DSS recognition are not likely to converge. We indeed invalidate an hypothesis which was essential in the only known convergence theorem of a discrete curvature estimator. The proof involves results from arithmetic properties of digital lines, digital convexity, combinatorics, continued fractions and random polytopes.