Optimisation of photometric stereo methods by non-convex variational minimisation

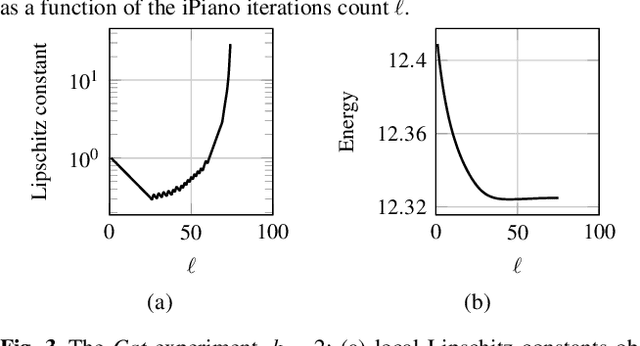
Estimating shape and appearance of a three dimensional object from a given set of images is a classic research topic that is still actively pursued. Among the various techniques available, PS is distinguished by the assumption that the underlying input images are taken from the same point of view but under different lighting conditions. The most common techniques provide the shape information in terms of surface normals. In this work, we instead propose to minimise a much more natural objective function, namely the reprojection error in terms of depth. Minimising the resulting non-trivial variational model for PS allows to recover the depth of the photographed scene directly. As a solving strategy, we follow an approach based on a recently published optimisation scheme for non-convex and non-smooth cost functions. The main contributions of our paper are of theoretical nature. A technical novelty in our framework is the usage of matrix differential calculus. We supplement our approach by a detailed convergence analysis of the resulting optimisation algorithm and discuss possibilities to ease the computational complexity. At hand of an experimental evaluation we discuss important properties of the method. Overall, our strategy achieves more accurate results than competing approaches. The experiments also highlights some practical aspects of the underlying optimisation algorithm that may be of interest in a more general context.

Clustering-Based Quantisation for PDE-Based Image Compression

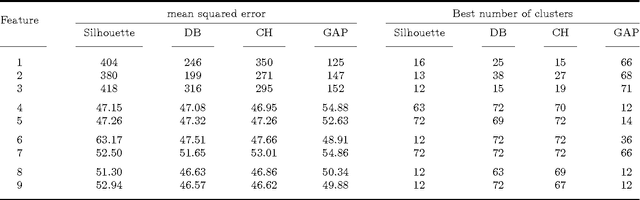
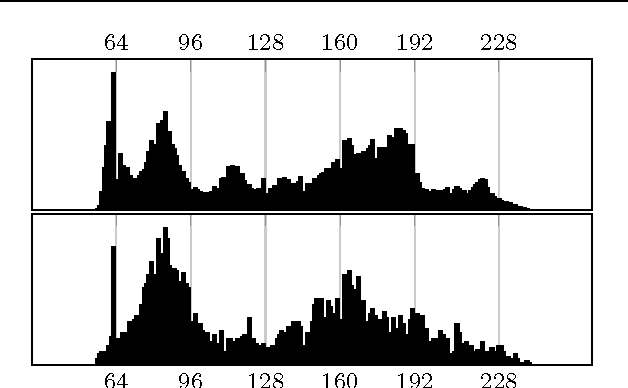
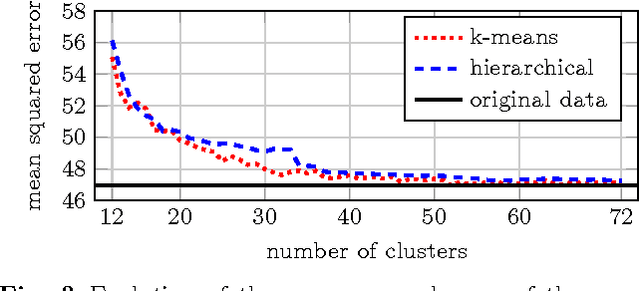
Finding optimal data for inpainting is a key problem in the context of partial differential equation based image compression. The data that yields the most accurate reconstruction is real-valued. Thus, quantisation models are mandatory to allow an efficient encoding. These can also be understood as challenging data clustering problems. Although clustering approaches are well suited for this kind of compression codecs, very few works actually consider them. Each pixel has a global impact on the reconstruction and optimal data locations are strongly correlated with their corresponding colour values. These facts make it hard to predict which feature works best. In this paper we discuss quantisation strategies based on popular methods such as k-means. We are lead to the central question which kind of feature vectors are best suited for image compression. To this end we consider choices such as the pixel values, the histogram or the colour map. Our findings show that the number of colours can be reduced significantly without impacting the reconstruction quality. Surprisingly, these benefits do not directly translate to a good image compression performance. The gains in the compression ratio are lost due to increased storage costs. This suggests that it is integral to evaluate the clustering on both, the reconstruction error and the final file size.

Bregman Iteration for Correspondence Problems: A Study of Optical Flow

Bregman iterations are known to yield excellent results for denoising, deblurring and compressed sensing tasks, but so far this technique has rarely been used for other image processing problems. In this paper we give a thorough description of the Bregman iteration, unifying thereby results of different authors within a common framework. Then we show how to adapt the split Bregman iteration, originally developed by Goldstein and Osher for image restoration purposes, to optical flow which is a fundamental correspondence problem in computer vision. We consider some classic and modern optical flow models and present detailed algorithms that exhibit the benefits of the Bregman iteration. By making use of the results of the Bregman framework, we address the issues of convergence and error estimation for the algorithms. Numerical examples complement the theoretical part.

Optimising Spatial and Tonal Data for PDE-based Inpainting

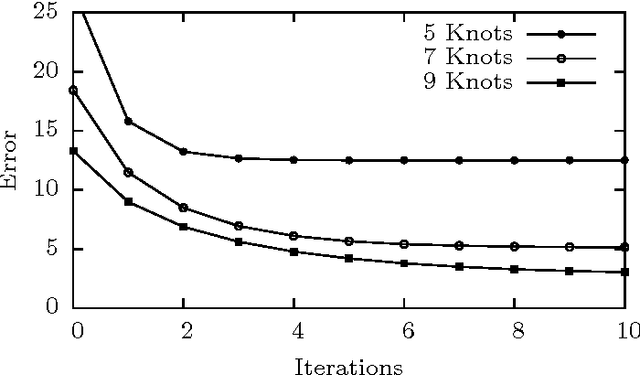
Some recent methods for lossy signal and image compression store only a few selected pixels and fill in the missing structures by inpainting with a partial differential equation (PDE). Suitable operators include the Laplacian, the biharmonic operator, and edge-enhancing anisotropic diffusion (EED). The quality of such approaches depends substantially on the selection of the data that is kept. Optimising this data in the domain and codomain gives rise to challenging mathematical problems that shall be addressed in our work. In the 1D case, we prove results that provide insights into the difficulty of this problem, and we give evidence that a splitting into spatial and tonal (i.e. function value) optimisation does hardly deteriorate the results. In the 2D setting, we present generic algorithms that achieve a high reconstruction quality even if the specified data is very sparse. To optimise the spatial data, we use a probabilistic sparsification, followed by a nonlocal pixel exchange that avoids getting trapped in bad local optima. After this spatial optimisation we perform a tonal optimisation that modifies the function values in order to reduce the global reconstruction error. For homogeneous diffusion inpainting, this comes down to a least squares problem for which we prove that it has a unique solution. We demonstrate that it can be found efficiently with a gradient descent approach that is accelerated with fast explicit diffusion (FED) cycles. Our framework allows to specify the desired density of the inpainting mask a priori. Moreover, is more generic than other data optimisation approaches for the sparse inpainting problem, since it can also be extended to nonlinear inpainting operators such as EED. This is exploited to achieve reconstructions with state-of-the-art quality. We also give an extensive literature survey on PDE-based image compression methods.