Image Compression with Isotropic and Anisotropic Shepard Inpainting

Inpainting-based codecs store sparse selected pixel data and decode by reconstructing the discarded image parts by inpainting. Successful codecs (coders and decoders) traditionally use inpainting operators that solve partial differential equations. This requires some numerical expertise if efficient implementations are necessary. Our goal is to investigate variants of Shepard inpainting as simple alternatives for inpainting-based compression. They can be implemented efficiently when we localise their weighting function. To turn them into viable codecs, we have to introduce novel extensions of classical Shepard interpolation that adapt successful ideas from previous codecs: Anisotropy allows direction-dependent inpainting, which improves reconstruction quality. Additionally, we incorporate data selection by subdivision as an efficient way to tailor the stored information to the image structure. On the encoding side, we introduce the novel concept of joint inpainting and prediction for isotropic Shepard codecs, where storage cost can be reduced based on intermediate inpainting results. In an ablation study, we show the usefulness of these individual contributions and demonstrate that they offer synergies which elevate the performance of Shepard inpainting to surprising levels. Our resulting approaches offer a more favourable trade-off between simplicity and quality than traditional inpainting-based codecs. Experiments show that they can outperform JPEG and JPEG2000 at high compression ratios.

Neuroexplicit Diffusion Models for Inpainting of Optical Flow Fields

Deep learning has revolutionized the field of computer vision by introducing large scale neural networks with millions of parameters. Training these networks requires massive datasets and leads to intransparent models that can fail to generalize. At the other extreme, models designed from partial differential equations (PDEs) embed specialized domain knowledge into mathematical equations and usually rely on few manually chosen hyperparameters. This makes them transparent by construction and if designed and calibrated carefully, they can generalize well to unseen scenarios. In this paper, we show how to bring model- and data-driven approaches together by combining the explicit PDE-based approaches with convolutional neural networks to obtain the best of both worlds. We illustrate a joint architecture for the task of inpainting optical flow fields and show that the combination of model- and data-driven modeling leads to an effective architecture. Our model outperforms both fully explicit and fully data-driven baselines in terms of reconstruction quality, robustness and amount of required training data. Averaging the endpoint error across different mask densities, our method outperforms the explicit baselines by 11-27%, the GAN baseline by 47% and the Probabilisitic Diffusion baseline by 42%. With that, our method sets a new state of the art for inpainting of optical flow fields from random masks.

Gaining Insights into Denoising by Inpainting

The filling-in effect of diffusion processes is a powerful tool for various image analysis tasks such as inpainting-based compression and dense optic flow computation. For noisy data, an interesting side effect occurs: The interpolated data have higher confidence, since they average information from many noisy sources. This observation forms the basis of our denoising by inpainting (DbI) framework. It averages multiple inpainting results from different noisy subsets. Our goal is to obtain fundamental insights into key properties of DbI and its connections to existing methods. Like in inpainting-based image compression, we choose homogeneous diffusion as a very simple inpainting operator that performs well for highly optimized data. We propose several strategies to choose the location of the selected pixels. Moreover, to improve the global approximation quality further, we also allow to change the function values of the noisy pixels. In contrast to traditional denoising methods that adapt the operator to the data, our approach adapts the data to the operator. Experimentally we show that replacing homogeneous diffusion inpainting by biharmonic inpainting does not improve the reconstruction quality. This again emphasizes the importance of data adaptivity over operator adaptivity. On the foundational side, we establish deterministic and probabilistic theories with convergence estimates. In the non-adaptive 1-D case, we derive equivalence results between DbI on shifted regular grids and classical homogeneous diffusion filtering via an explicit relation between the density and the diffusion time.

Generalised Probabilistic Diffusion Scale-Spaces

Probabilistic diffusion models excel at sampling new images from learned distributions. Originally motivated by drift-diffusion concepts from physics, they apply image perturbations such as noise and blur in a forward process that results in a tractable probability distribution. A corresponding learned reverse process generates images and can be conditioned on side information, which leads to a wide variety of practical applications. Most of the research focus currently lies on practice-oriented extensions. In contrast, the theoretical background remains largely unexplored, in particular the relations to drift-diffusion. In order to shed light on these connections to classical image filtering, we propose a generalised scale-space theory for probabilistic diffusion models. Moreover, we show conceptual and empirical connections to diffusion and osmosis filters.

Efficient Neural Generation of 4K Masks for Homogeneous Diffusion Inpainting

With well-selected data, homogeneous diffusion inpainting can reconstruct images from sparse data with high quality. While 4K colour images of size 3840 x 2160 can already be inpainted in real time, optimising the known data for applications like image compression remains challenging: Widely used stochastic strategies can take days for a single 4K image. Recently, a first neural approach for this so-called mask optimisation problem offered high speed and good quality for small images. It trains a mask generation network with the help of a neural inpainting surrogate. However, these mask networks can only output masks for the resolution and mask density they were trained for. We solve these problems and enable mask optimisation for high-resolution images through a neuroexplicit coarse-to-fine strategy. Additionally, we improve the training and interpretability of mask networks by including a numerical inpainting solver directly into the network. This allows to generate masks for 4K images in around 0.6 seconds while exceeding the quality of stochastic methods on practically relevant densities. Compared to popular existing approaches, this is an acceleration of up to four orders of magnitude.

Generalised Scale-Space Properties for Probabilistic Diffusion Models

Probabilistic diffusion models enjoy increasing popularity in the deep learning community. They generate convincing samples from a learned distribution of input images with a wide field of practical applications. Originally, these approaches were motivated from drift-diffusion processes, but these origins find less attention in recent, practice-oriented publications. We investigate probabilistic diffusion models from the viewpoint of scale-space research and show that they fulfil generalised scale-space properties on evolving probability distributions. Moreover, we discuss similarities and differences between interpretations of the physical core concept of drift-diffusion in the deep learning and model-based world. To this end, we examine relations of probabilistic diffusion to osmosis filters.

Image Blending with Osmosis

Image blending is an integral part of many multi-image applications such as panorama stitching or remote image acquisition processes. In such scenarios, multiple images are connected at predefined boundaries to form a larger image. A convincing transition between these boundaries may be challenging, since each image might have been acquired under different conditions or even by different devices. We propose the first blending approach based on osmosis filters. These drift-diffusion processes define an image evolution with a non-trivial steady state. For our blending purposes, we explore several ways to compose drift vector fields based on the derivatives of our input images. These vector fields guide the evolution such that the steady state yields a convincing blended result. Our method benefits from the well-founded theoretical results for osmosis, which include useful invariances under multiplicative changes of the colour values. Experiments on real-world data show that this yields better quality than traditional gradient domain blending, especially under challenging illumination conditions.

Deep Spatial and Tonal Data Optimisation for Homogeneous Diffusion Inpainting

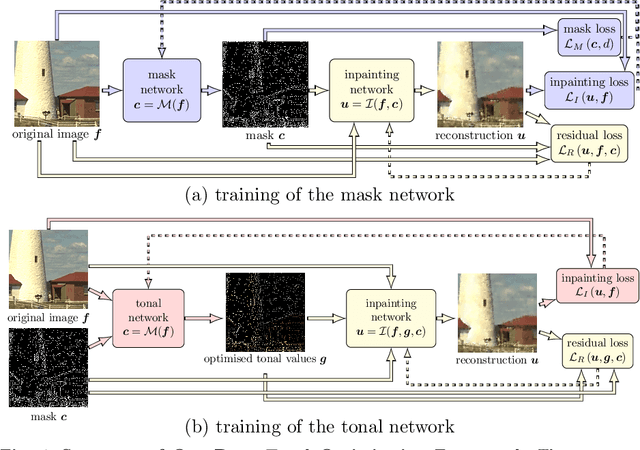
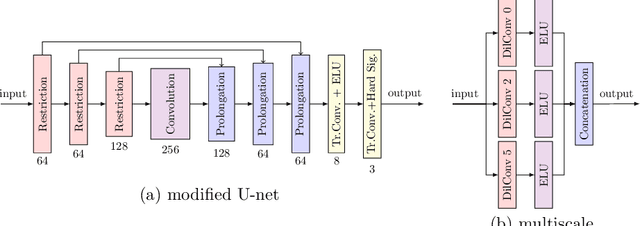
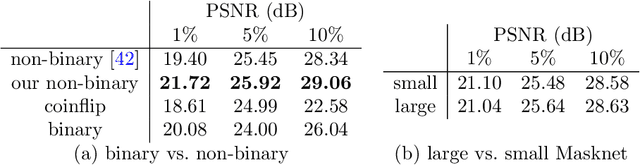
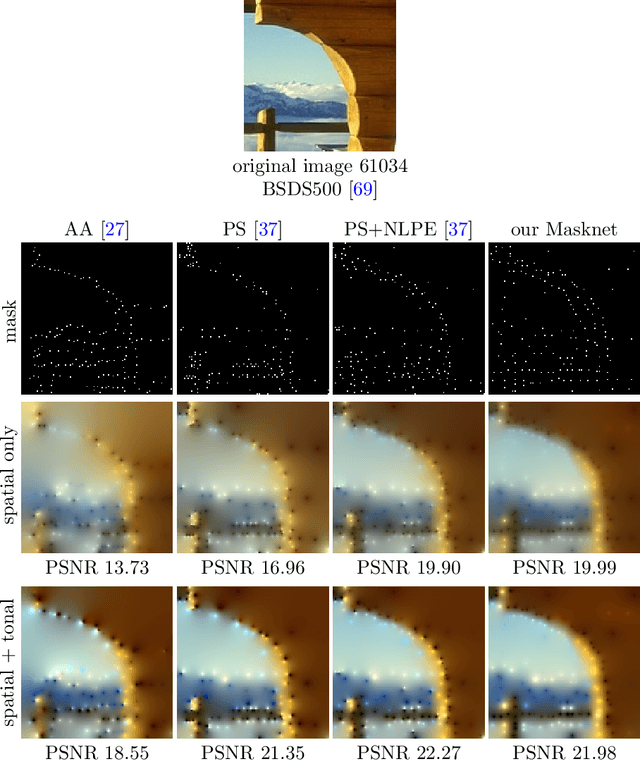
Diffusion-based inpainting can reconstruct missing image areas with high quality from sparse data, provided that their location and their values are well optimised. This is particularly useful for applications such as image compression, where the original image is known. Selecting the known data constitutes a challenging optimisation problem, that has so far been only investigated with model-based approaches. So far, these methods require a choice between either high quality or high speed since qualitatively convincing algorithms rely on many time-consuming inpaintings. We propose the first neural network architecture that allows fast optimisation of pixel positions and pixel values for homogeneous diffusion inpainting. During training, we combine two optimisation networks with a neural network-based surrogate solver for diffusion inpainting. This novel concept allows us to perform backpropagation based on inpainting results that approximate the solution of the inpainting equation. Without the need for a single inpainting during test time, our deep optimisation combines the high quality of model-based approaches with real-time performance.

A Wasserstein GAN for Joint Learning of Inpainting and its Spatial Optimisation

Classic image inpainting is a restoration method that reconstructs missing image parts. However, a carefully selected mask of known pixels that yield a high quality inpainting can also act as a sparse image representation. This challenging spatial optimisation problem is essential for practical applications such as compression. So far, it has been almost exclusively addressed by model-based approaches. First attempts with neural networks seem promising, but are tailored towards specific inpainting operators or require postprocessing. To address this issue, we propose the first generative adversarial network for spatial inpainting data optimisation. In contrast to previous approaches, it allows joint training of an inpainting generator and a corresponding mask optimisation network. With a Wasserstein distance, we ensure that our inpainting results accurately reflect the statistics of natural images. This yields significant improvements in visual quality and speed over conventional stochastic models and also outperforms current spatial optimisation networks.

Learning Sparse Masks for Diffusion-based Image Inpainting

Diffusion-based inpainting is a powerful tool for the reconstruction of images from sparse data. Its quality strongly depends on the choice of known data. Optimising their spatial location -- the inpainting mask -- is challenging. A commonly used tool for this task are stochastic optimisation strategies. However, they are slow as they compute multiple inpainting results. We provide a remedy in terms of a learned mask generation model. By emulating the complete inpainting pipeline with two networks for mask generation and neural surrogate inpainting, we obtain a model for highly efficient adaptive mask generation. Experiments indicate that our model can achieve competitive quality with an acceleration by as much as four orders of magnitude. Our findings serve as a basis for making diffusion-based inpainting more attractive for various applications such as image compression, where fast encoding is highly desirable.