Efficient Parallel Algorithms for Inpainting-Based Representations of 4K Images -- Part I: Homogeneous Diffusion Inpainting

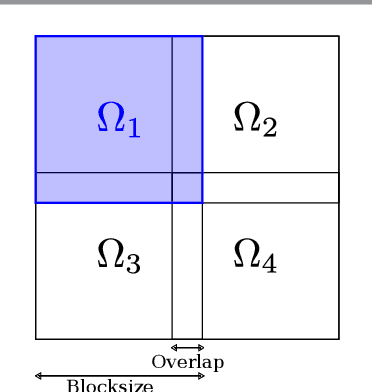
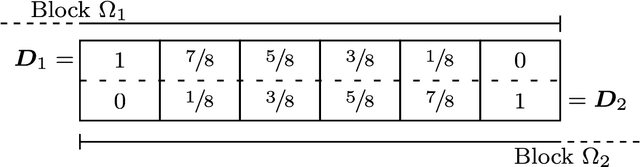
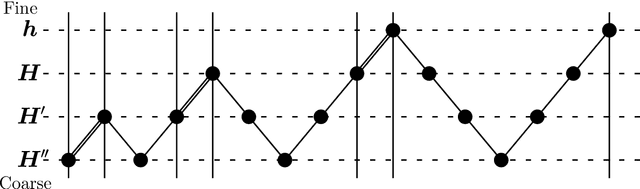
In recent years inpainting-based compression methods have been shown to be a viable alternative to classical codecs such as JPEG and JPEG2000. Unlike transform-based codecs, which store coefficients in the transform domain, inpainting-based approaches store a small subset of the original image pixels and reconstruct the image from those by using a suitable inpainting operator. A good candidate for such an inpainting operator is homogeneous diffusion inpainting, as it is simple, theoretically well-motivated, and can achieve good reconstruction quality for optimized data. However, a major challenge has been to design fast solvers for homogeneous diffusion inpainting that scale to 4K image resolution ($3840 \times 2160$ pixels) and are real-time capable. We overcome this with a careful adaptation and fusion of two of the most efficient concept from numerical analysis: multigrid and domain decomposition. Our domain decomposition algorithm efficiently utilizes GPU parallelism by solving inpainting problems on small overlapping blocks. Unlike simple block decomposition strategies such as the ones in JPEG, our approach yields block artifact-free reconstructions. Furthermore, embedding domain decomposition in a full multigrid scheme provides global interactions and allows us to achieve optimal convergence by reducing both low- and high-frequency errors at the same rate. We are able to achieve 4K color image reconstruction at more than $60$ frames per second even from very sparse data - something which has been previously unfeasible.

Efficient Parallel Algorithms for Inpainting-Based Representations of 4K Images -- Part II: Spatial and Tonal Data Optimization

Homogeneous diffusion inpainting can reconstruct missing image areas with high quality from a sparse subset of known pixels, provided that their location as well as their gray or color values are well optimized. This property is exploited in inpainting-based image compression, which is a promising alternative to classical transform-based codecs such as JPEG and JPEG2000. However, optimizing the inpainting data is a challenging task. Current approaches are either quite slow or do not produce high quality results. As a remedy we propose fast spatial and tonal optimization algorithms for homogeneous diffusion inpainting that efficiently utilize GPU parallelism, with a careful adaptation of some of the most successful numerical concepts. We propose a densification strategy using ideas from error-map dithering combined with a Delaunay triangulation for the spatial optimization. For the tonal optimization we design a domain decomposition solver that solves the corresponding normal equations in a matrix-free fashion and supplement it with a Voronoi-based initialization strategy. With our proposed methods we are able to generate high quality inpainting masks for homogeneous diffusion and optimized tonal values in a runtime that outperforms prior state-of-the-art by a wide margin.

Gaining Insights into Denoising by Inpainting

The filling-in effect of diffusion processes is a powerful tool for various image analysis tasks such as inpainting-based compression and dense optic flow computation. For noisy data, an interesting side effect occurs: The interpolated data have higher confidence, since they average information from many noisy sources. This observation forms the basis of our denoising by inpainting (DbI) framework. It averages multiple inpainting results from different noisy subsets. Our goal is to obtain fundamental insights into key properties of DbI and its connections to existing methods. Like in inpainting-based image compression, we choose homogeneous diffusion as a very simple inpainting operator that performs well for highly optimized data. We propose several strategies to choose the location of the selected pixels. Moreover, to improve the global approximation quality further, we also allow to change the function values of the noisy pixels. In contrast to traditional denoising methods that adapt the operator to the data, our approach adapts the data to the operator. Experimentally we show that replacing homogeneous diffusion inpainting by biharmonic inpainting does not improve the reconstruction quality. This again emphasizes the importance of data adaptivity over operator adaptivity. On the foundational side, we establish deterministic and probabilistic theories with convergence estimates. In the non-adaptive 1-D case, we derive equivalence results between DbI on shifted regular grids and classical homogeneous diffusion filtering via an explicit relation between the density and the diffusion time.

Optimising Different Feature Types for Inpainting-based Image Representations

Inpainting-based image compression is a promising alternative to classical transform-based lossy codecs. Typically it stores a carefully selected subset of all pixel locations and their colour values. In the decoding phase the missing information is reconstructed by an inpainting process such as homogeneous diffusion inpainting. Optimising the stored data is the key for achieving good performance. A few heuristic approaches also advocate alternative feature types such as derivative data and construct dedicated inpainting concepts. However, one still lacks a general approach that allows to optimise and inpaint the data simultaneously w.r.t. a collection of different feature types, their locations, and their values. Our paper closes this gap. We introduce a generalised inpainting process that can handle arbitrary features which can be expressed as linear equality constraints. This includes e.g. colour values and derivatives of any order. We propose a fully automatic algorithm that aims at finding the optimal features from a given collection as well as their locations and their function values within a specified total feature density. Its performance is demonstrated with a novel set of features that also includes local averages. Our experiments show that it clearly outperforms the popular inpainting with optimised colour data with the same density.

Efficient Data Optimisation for Harmonic Inpainting with Finite Elements

Harmonic inpainting with optimised data is very popular for inpainting-based image compression. We improve this approach in three important aspects. Firstly, we replace the standard finite differences discretisation by a finite element method with triangle elements. This does not only speed up inpainting and data selection, but even improves the reconstruction quality. Secondly, we propose highly efficient algorithms for spatial and tonal data optimisation that are several orders of magnitude faster than state-of-the-art methods. Last but not least, we show that our algorithms also allow working with very large images. This has previously been impractical due to the memory and runtime requirements of prior algorithms.