Anisotropic Diffusion Stencils: From Simple Derivations over Stability Estimates to ResNet Implementations

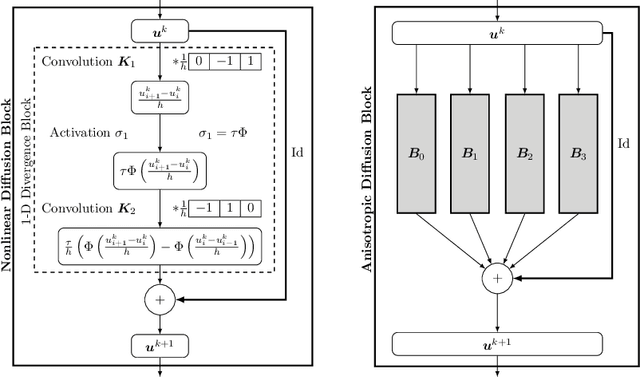
Anisotropic diffusion processes with a diffusion tensor are important in image analysis, physics, and engineering. However, their numerical approximation has a strong impact on dissipative artefacts and deviations from rotation invariance. In this work, we study a large family of finite difference discretisations on a 3 x 3 stencil. We derive it by splitting 2-D anisotropic diffusion into four 1-D diffusions. The resulting stencil class involves one free parameter and covers a wide range of existing discretisations. It comprises the full stencil family of Weickert et al. (2013) and shows that their two parameters contain redundancy. Furthermore, we establish a bound on the spectral norm of the matrix corresponding to the stencil. This gives time step size limits that guarantee stability of an explicit scheme in the Euclidean norm. Our directional splitting also allows a very natural translation of the explicit scheme into ResNet blocks. Employing neural network libraries enables simple and highly efficient parallel implementations on GPUs.

Efficient Neural Generation of 4K Masks for Homogeneous Diffusion Inpainting

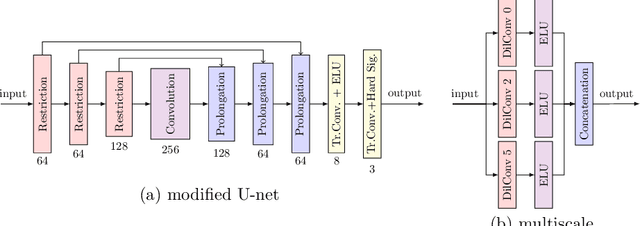
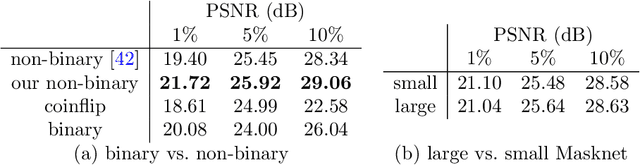
With well-selected data, homogeneous diffusion inpainting can reconstruct images from sparse data with high quality. While 4K colour images of size 3840 x 2160 can already be inpainted in real time, optimising the known data for applications like image compression remains challenging: Widely used stochastic strategies can take days for a single 4K image. Recently, a first neural approach for this so-called mask optimisation problem offered high speed and good quality for small images. It trains a mask generation network with the help of a neural inpainting surrogate. However, these mask networks can only output masks for the resolution and mask density they were trained for. We solve these problems and enable mask optimisation for high-resolution images through a neuroexplicit coarse-to-fine strategy. Additionally, we improve the training and interpretability of mask networks by including a numerical inpainting solver directly into the network. This allows to generate masks for 4K images in around 0.6 seconds while exceeding the quality of stochastic methods on practically relevant densities. Compared to popular existing approaches, this is an acceleration of up to four orders of magnitude.

Deep Spatial and Tonal Data Optimisation for Homogeneous Diffusion Inpainting

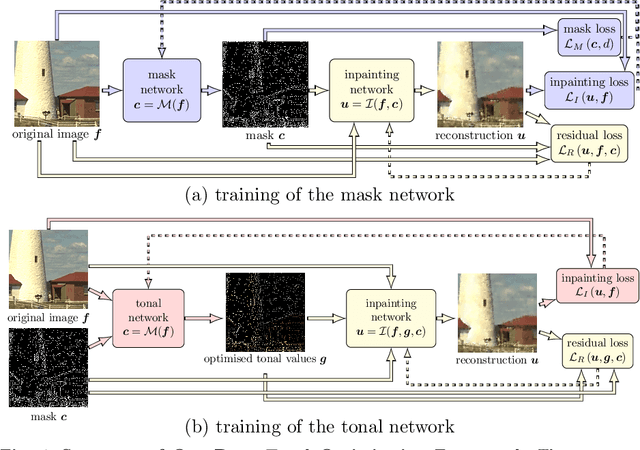
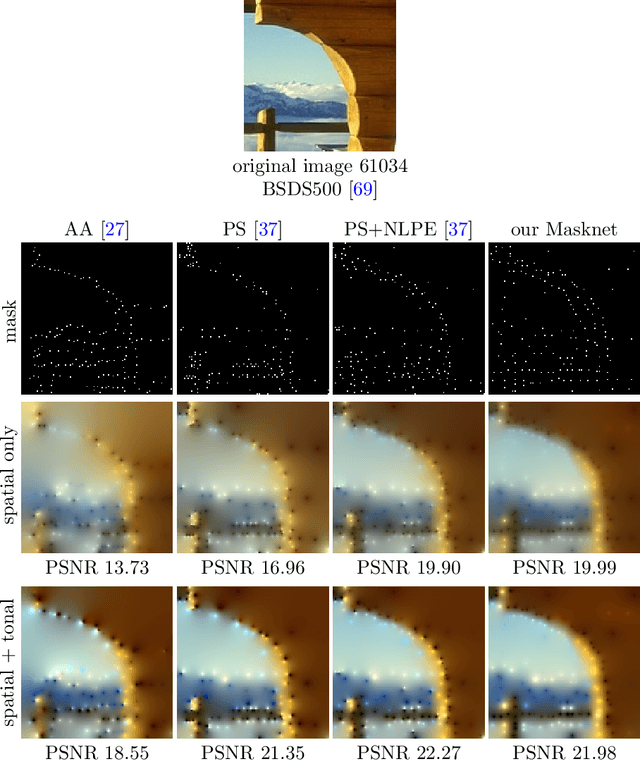
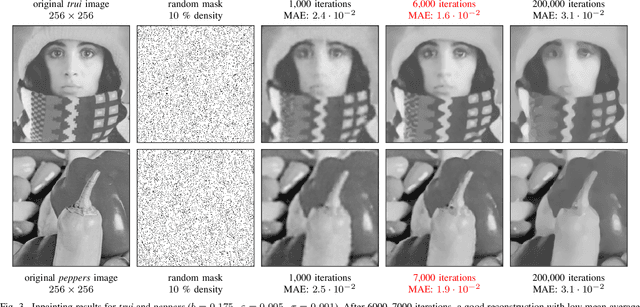
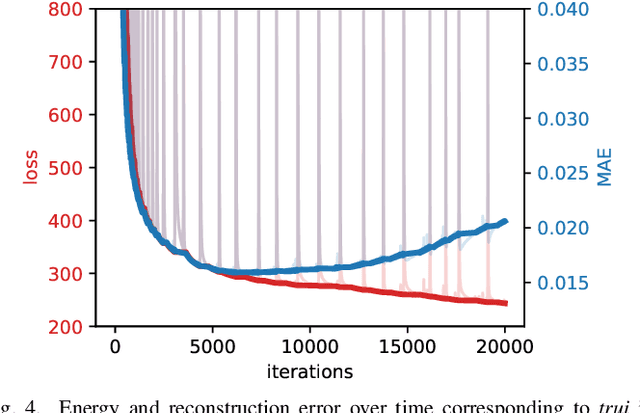
Diffusion-based inpainting can reconstruct missing image areas with high quality from sparse data, provided that their location and their values are well optimised. This is particularly useful for applications such as image compression, where the original image is known. Selecting the known data constitutes a challenging optimisation problem, that has so far been only investigated with model-based approaches. So far, these methods require a choice between either high quality or high speed since qualitatively convincing algorithms rely on many time-consuming inpaintings. We propose the first neural network architecture that allows fast optimisation of pixel positions and pixel values for homogeneous diffusion inpainting. During training, we combine two optimisation networks with a neural network-based surrogate solver for diffusion inpainting. This novel concept allows us to perform backpropagation based on inpainting results that approximate the solution of the inpainting equation. Without the need for a single inpainting during test time, our deep optimisation combines the high quality of model-based approaches with real-time performance.

CNN-based Euler's Elastica Inpainting with Deep Energy and Deep Image Prior

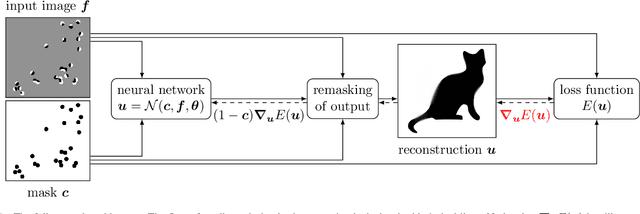
Euler's elastica constitute an appealing variational image inpainting model. It minimises an energy that involves the total variation as well as the level line curvature. These components are transparent and make it attractive for shape completion tasks. However, its gradient flow is a singular, anisotropic, and nonlinear PDE of fourth order, which is numerically challenging: It is difficult to find efficient algorithms that offer sharp edges and good rotation invariance. As a remedy, we design the first neural algorithm that simulates inpainting with Euler's Elastica. We use the deep energy concept which employs the variational energy as neural network loss. Furthermore, we pair it with a deep image prior where the network architecture itself acts as a prior. This yields better inpaintings by steering the optimisation trajectory closer to the desired solution. Our results are qualitatively on par with state-of-the-art algorithms on elastica-based shape completion. They combine good rotation invariance with sharp edges. Moreover, we benefit from the high efficiency and effortless parallelisation within a neural framework. Our neural elastica approach only requires 3x3 central difference stencils. It is thus much simpler than other well-performing algorithms for elastica inpainting. Last but not least, it is unsupervised as it requires no ground truth training data.

Designing Rotationally Invariant Neural Networks from PDEs and Variational Methods

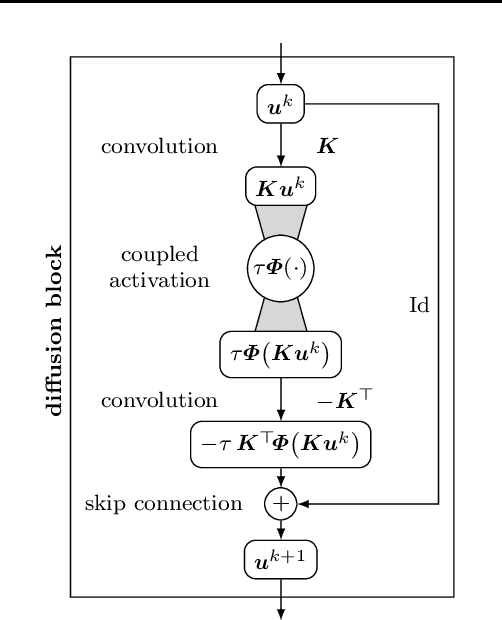
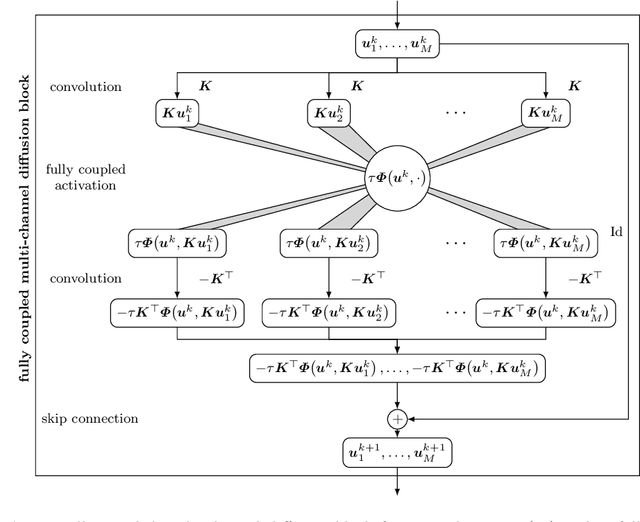
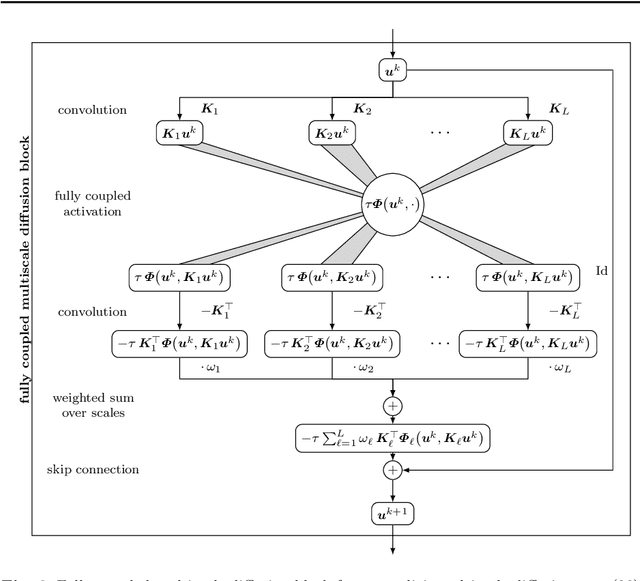
Partial differential equation (PDE) models and their associated variational energy formulations are often rotationally invariant by design. This ensures that a rotation of the input results in a corresponding rotation of the output, which is desirable in applications such as image analysis. Convolutional neural networks (CNNs) do not share this property, and existing remedies are often complex. The goal of our paper is to investigate how diffusion and variational models achieve rotation invariance and transfer these ideas to neural networks. As a core novelty we propose activation functions which couple network channels by combining information from several oriented filters. This guarantees rotation invariance within the basic building blocks of the networks while still allowing for directional filtering. The resulting neural architectures are inherently rotationally invariant. With only a few small filters, they can achieve the same invariance as existing techniques which require a fine-grained sampling of orientations. Our findings help to translate diffusion and variational models into mathematically well-founded network architectures, and provide novel concepts for model-based CNN design.

Connections between Numerical Algorithms for PDEs and Neural Networks

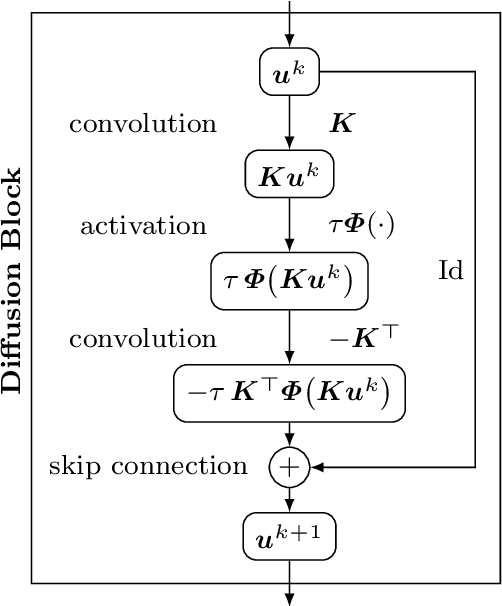
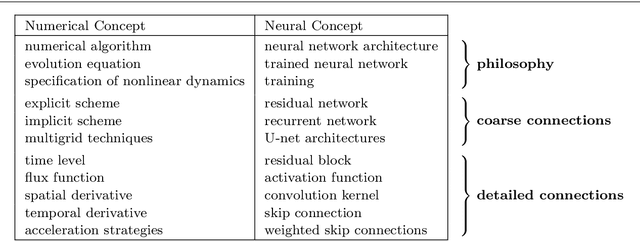
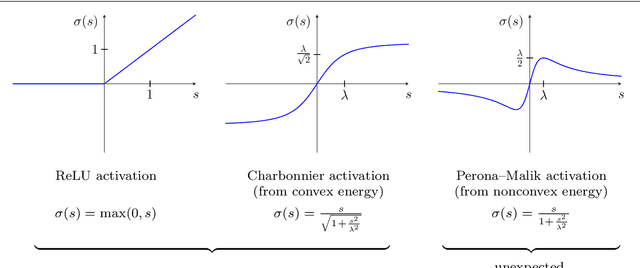
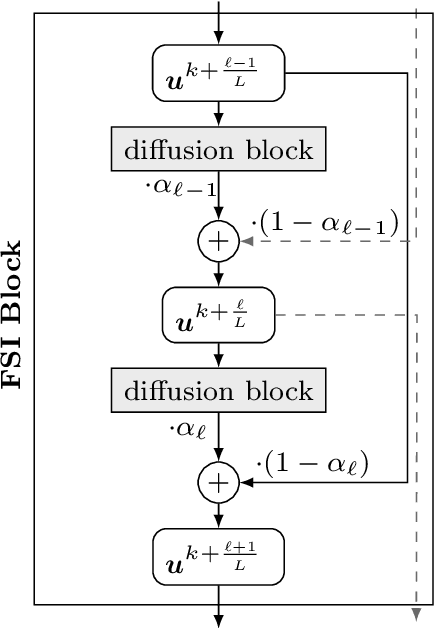
We investigate numerous structural connections between numerical algorithms for partial differential equations (PDEs) and neural architectures. Our goal is to transfer the rich set of mathematical foundations from the world of PDEs to neural networks. Besides structural insights we provide concrete examples and experimental evaluations of the resulting architectures. Using the example of generalised nonlinear diffusion in 1D, we consider explicit schemes, acceleration strategies thereof, implicit schemes, and multigrid approaches. We connect these concepts to residual networks, recurrent neural networks, and U-net architectures. Our findings inspire a symmetric residual network design with provable stability guarantees and justify the effectiveness of skip connections in neural networks from a numerical perspective. Moreover, we present U-net architectures that implement multigrid techniques for learning efficient solutions of partial differential equation models, and motivate uncommon design choices such as trainable nonmonotone activation functions. Experimental evaluations show that the proposed architectures save half of the trainable parameters and can thus outperform standard ones with the same model complexity. Our considerations serve as a basis for explaining the success of popular neural architectures and provide a blueprint for developing new mathematically well-founded neural building blocks.

Translating Numerical Concepts for PDEs into Neural Architectures

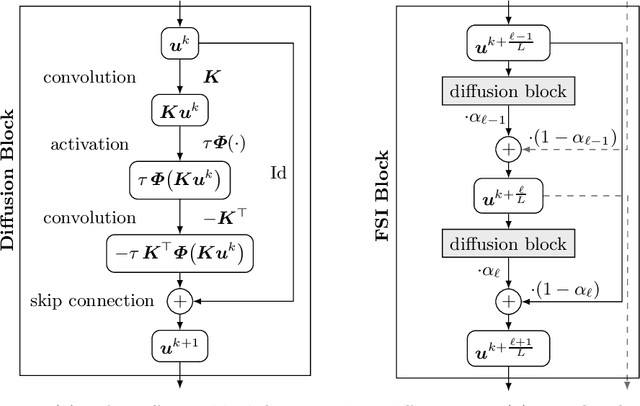
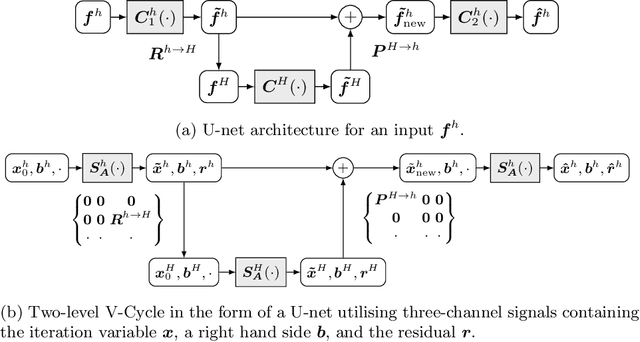
We investigate what can be learned from translating numerical algorithms into neural networks. On the numerical side, we consider explicit, accelerated explicit, and implicit schemes for a general higher order nonlinear diffusion equation in 1D, as well as linear multigrid methods. On the neural network side, we identify corresponding concepts in terms of residual networks (ResNets), recurrent networks, and U-nets. These connections guarantee Euclidean stability of specific ResNets with a transposed convolution layer structure in each block. We present three numerical justifications for skip connections: as time discretisations in explicit schemes, as extrapolation mechanisms for accelerating those methods, and as recurrent connections in fixed point solvers for implicit schemes. Last but not least, we also motivate uncommon design choices such as nonmonotone activation functions. Our findings give a numerical perspective on the success of modern neural network architectures, and they provide design criteria for stable networks.