Anisotropic Diffusion Stencils: From Simple Derivations over Stability Estimates to ResNet Implementations
Paper and Code
Sep 13, 2023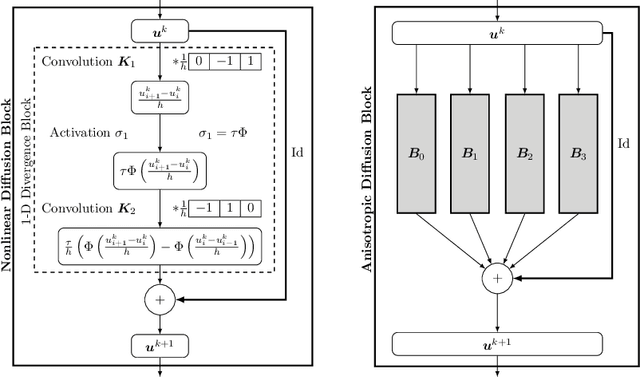
Anisotropic diffusion processes with a diffusion tensor are important in image analysis, physics, and engineering. However, their numerical approximation has a strong impact on dissipative artefacts and deviations from rotation invariance. In this work, we study a large family of finite difference discretisations on a 3 x 3 stencil. We derive it by splitting 2-D anisotropic diffusion into four 1-D diffusions. The resulting stencil class involves one free parameter and covers a wide range of existing discretisations. It comprises the full stencil family of Weickert et al. (2013) and shows that their two parameters contain redundancy. Furthermore, we establish a bound on the spectral norm of the matrix corresponding to the stencil. This gives time step size limits that guarantee stability of an explicit scheme in the Euclidean norm. Our directional splitting also allows a very natural translation of the explicit scheme into ResNet blocks. Employing neural network libraries enables simple and highly efficient parallel implementations on GPUs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge