Image Compression with Isotropic and Anisotropic Shepard Inpainting

Inpainting-based codecs store sparse selected pixel data and decode by reconstructing the discarded image parts by inpainting. Successful codecs (coders and decoders) traditionally use inpainting operators that solve partial differential equations. This requires some numerical expertise if efficient implementations are necessary. Our goal is to investigate variants of Shepard inpainting as simple alternatives for inpainting-based compression. They can be implemented efficiently when we localise their weighting function. To turn them into viable codecs, we have to introduce novel extensions of classical Shepard interpolation that adapt successful ideas from previous codecs: Anisotropy allows direction-dependent inpainting, which improves reconstruction quality. Additionally, we incorporate data selection by subdivision as an efficient way to tailor the stored information to the image structure. On the encoding side, we introduce the novel concept of joint inpainting and prediction for isotropic Shepard codecs, where storage cost can be reduced based on intermediate inpainting results. In an ablation study, we show the usefulness of these individual contributions and demonstrate that they offer synergies which elevate the performance of Shepard inpainting to surprising levels. Our resulting approaches offer a more favourable trade-off between simplicity and quality than traditional inpainting-based codecs. Experiments show that they can outperform JPEG and JPEG2000 at high compression ratios.

Generative AI Models: Opportunities and Risks for Industry and Authorities

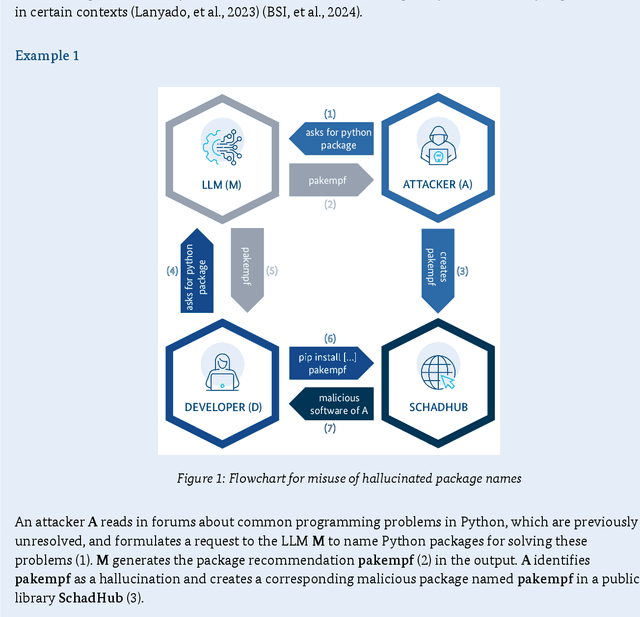
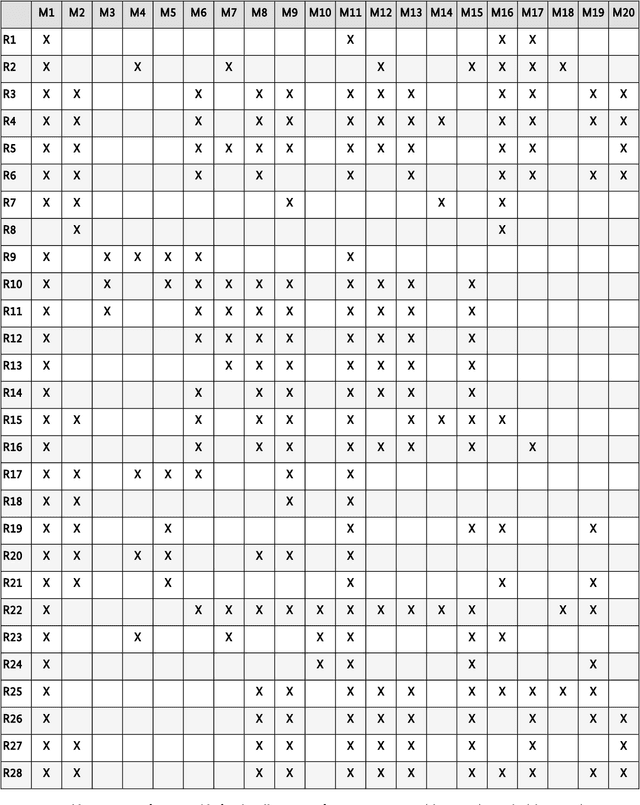
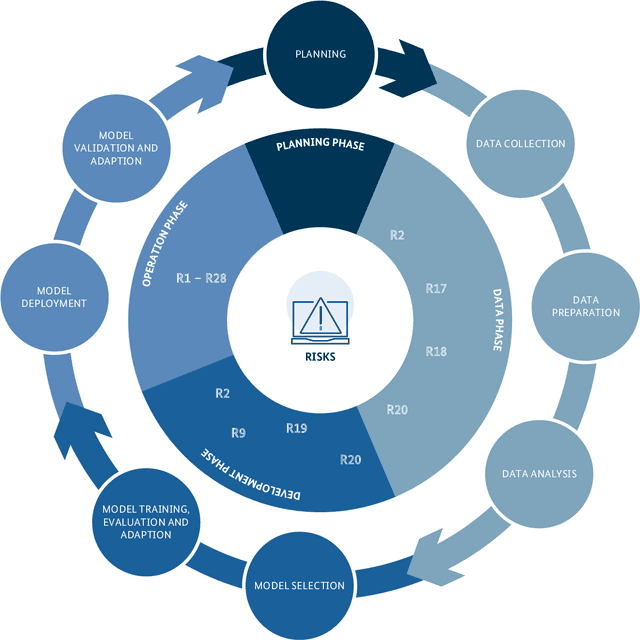
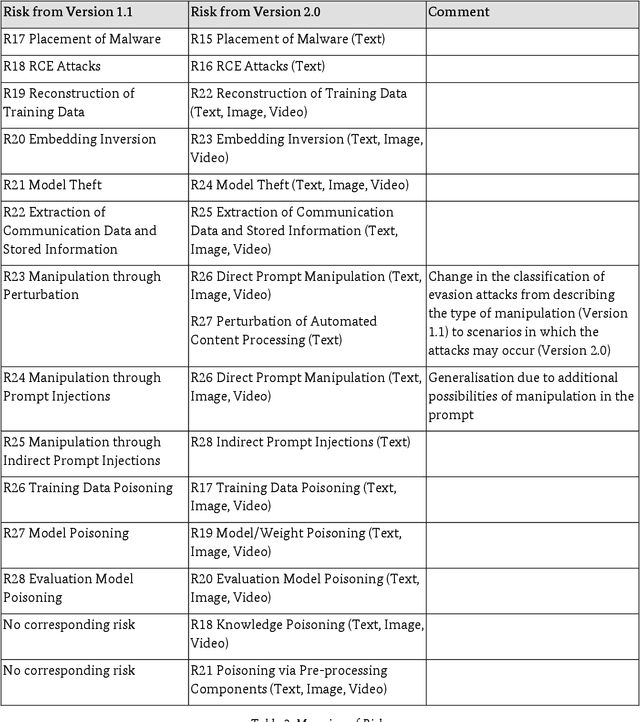
Generative AI models are capable of performing a wide range of tasks that traditionally require creativity and human understanding. They learn patterns from existing data during training and can subsequently generate new content such as texts, images, and music that follow these patterns. Due to their versatility and generally high-quality results, they, on the one hand, represent an opportunity for digitalization. On the other hand, the use of generative AI models introduces novel IT security risks that need to be considered for a comprehensive analysis of the threat landscape in relation to IT security. In response to this risk potential, companies or authorities using them should conduct an individual risk analysis before integrating generative AI into their workflows. The same applies to developers and operators, as many risks in the context of generative AI have to be taken into account at the time of development or can only be influenced by the operating company. Based on this, existing security measures can be adjusted, and additional measures can be taken.

Deep Spatial and Tonal Data Optimisation for Homogeneous Diffusion Inpainting

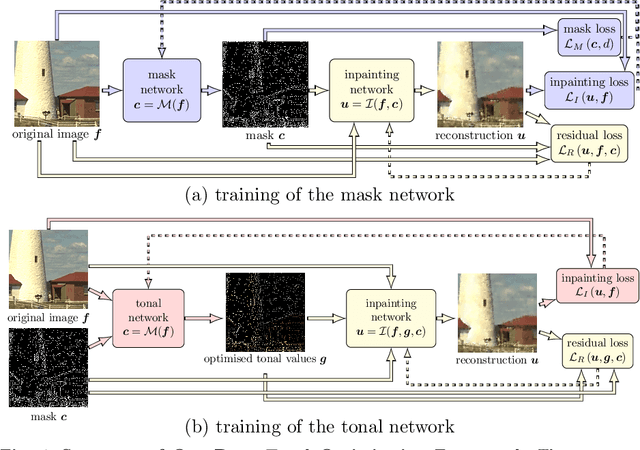
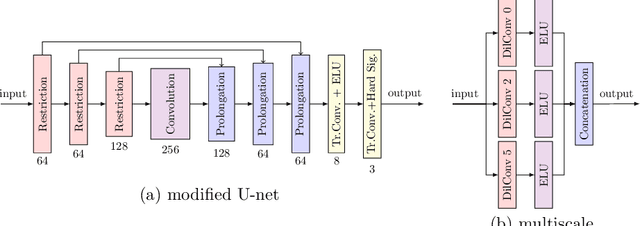
Diffusion-based inpainting can reconstruct missing image areas with high quality from sparse data, provided that their location and their values are well optimised. This is particularly useful for applications such as image compression, where the original image is known. Selecting the known data constitutes a challenging optimisation problem, that has so far been only investigated with model-based approaches. So far, these methods require a choice between either high quality or high speed since qualitatively convincing algorithms rely on many time-consuming inpaintings. We propose the first neural network architecture that allows fast optimisation of pixel positions and pixel values for homogeneous diffusion inpainting. During training, we combine two optimisation networks with a neural network-based surrogate solver for diffusion inpainting. This novel concept allows us to perform backpropagation based on inpainting results that approximate the solution of the inpainting equation. Without the need for a single inpainting during test time, our deep optimisation combines the high quality of model-based approaches with real-time performance.

CNN-based Euler's Elastica Inpainting with Deep Energy and Deep Image Prior

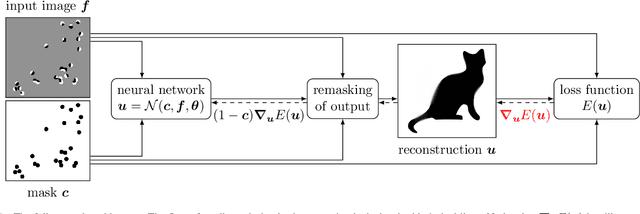
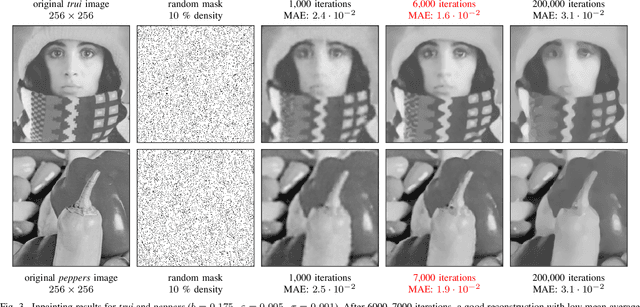
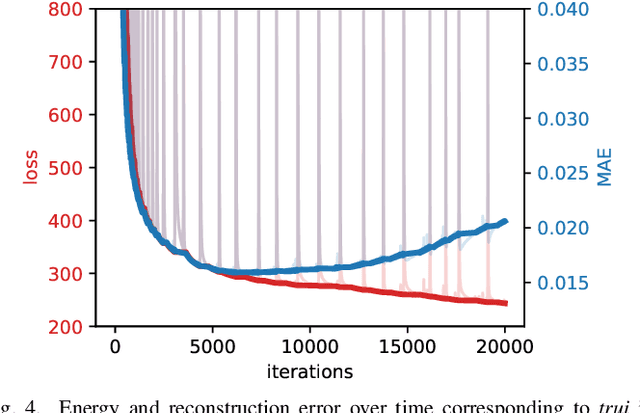
Euler's elastica constitute an appealing variational image inpainting model. It minimises an energy that involves the total variation as well as the level line curvature. These components are transparent and make it attractive for shape completion tasks. However, its gradient flow is a singular, anisotropic, and nonlinear PDE of fourth order, which is numerically challenging: It is difficult to find efficient algorithms that offer sharp edges and good rotation invariance. As a remedy, we design the first neural algorithm that simulates inpainting with Euler's Elastica. We use the deep energy concept which employs the variational energy as neural network loss. Furthermore, we pair it with a deep image prior where the network architecture itself acts as a prior. This yields better inpaintings by steering the optimisation trajectory closer to the desired solution. Our results are qualitatively on par with state-of-the-art algorithms on elastica-based shape completion. They combine good rotation invariance with sharp edges. Moreover, we benefit from the high efficiency and effortless parallelisation within a neural framework. Our neural elastica approach only requires 3x3 central difference stencils. It is thus much simpler than other well-performing algorithms for elastica inpainting. Last but not least, it is unsupervised as it requires no ground truth training data.

Learning Sparse Masks for Diffusion-based Image Inpainting

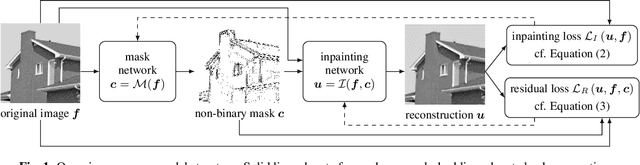
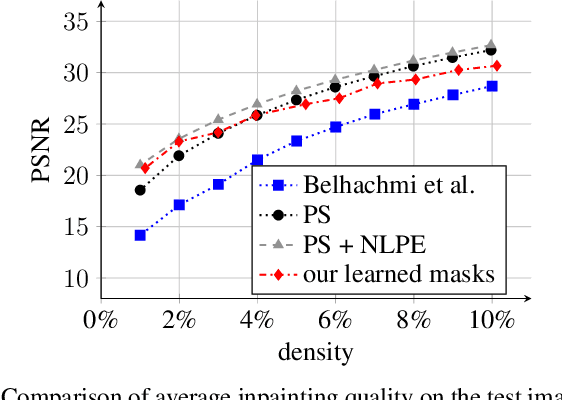
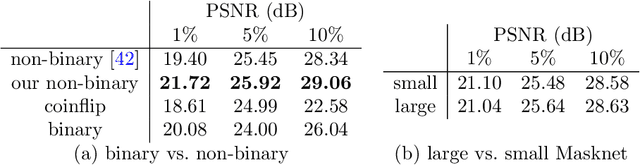
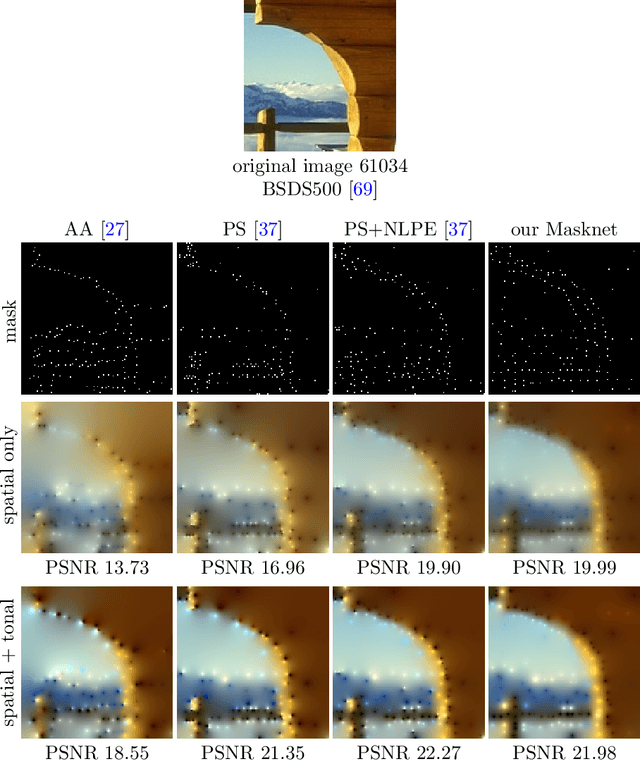
Diffusion-based inpainting is a powerful tool for the reconstruction of images from sparse data. Its quality strongly depends on the choice of known data. Optimising their spatial location -- the inpainting mask -- is challenging. A commonly used tool for this task are stochastic optimisation strategies. However, they are slow as they compute multiple inpainting results. We provide a remedy in terms of a learned mask generation model. By emulating the complete inpainting pipeline with two networks for mask generation and neural surrogate inpainting, we obtain a model for highly efficient adaptive mask generation. Experiments indicate that our model can achieve competitive quality with an acceleration by as much as four orders of magnitude. Our findings serve as a basis for making diffusion-based inpainting more attractive for various applications such as image compression, where fast encoding is highly desirable.

Designing Rotationally Invariant Neural Networks from PDEs and Variational Methods

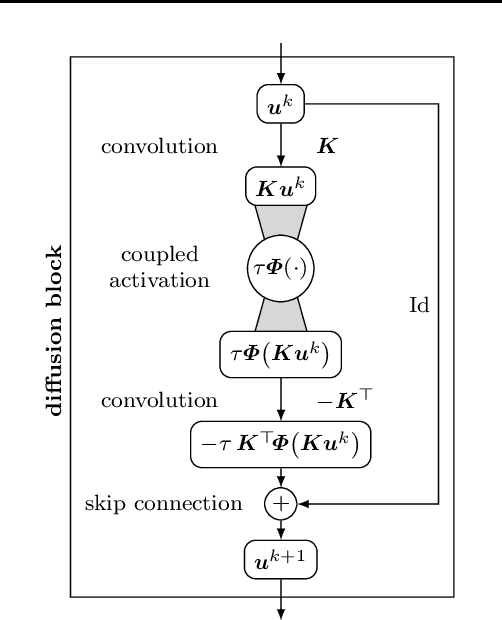
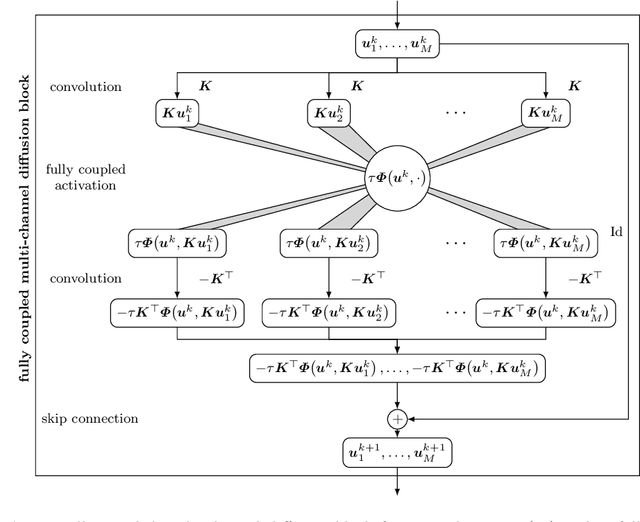
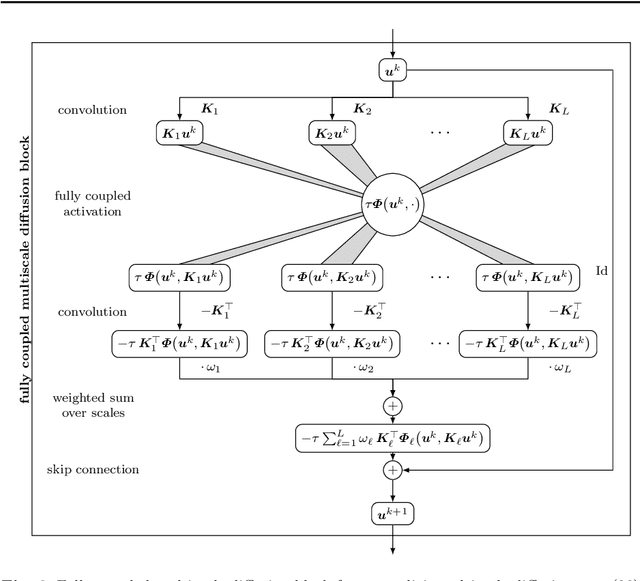
Partial differential equation (PDE) models and their associated variational energy formulations are often rotationally invariant by design. This ensures that a rotation of the input results in a corresponding rotation of the output, which is desirable in applications such as image analysis. Convolutional neural networks (CNNs) do not share this property, and existing remedies are often complex. The goal of our paper is to investigate how diffusion and variational models achieve rotation invariance and transfer these ideas to neural networks. As a core novelty we propose activation functions which couple network channels by combining information from several oriented filters. This guarantees rotation invariance within the basic building blocks of the networks while still allowing for directional filtering. The resulting neural architectures are inherently rotationally invariant. With only a few small filters, they can achieve the same invariance as existing techniques which require a fine-grained sampling of orientations. Our findings help to translate diffusion and variational models into mathematically well-founded network architectures, and provide novel concepts for model-based CNN design.

Connections between Numerical Algorithms for PDEs and Neural Networks

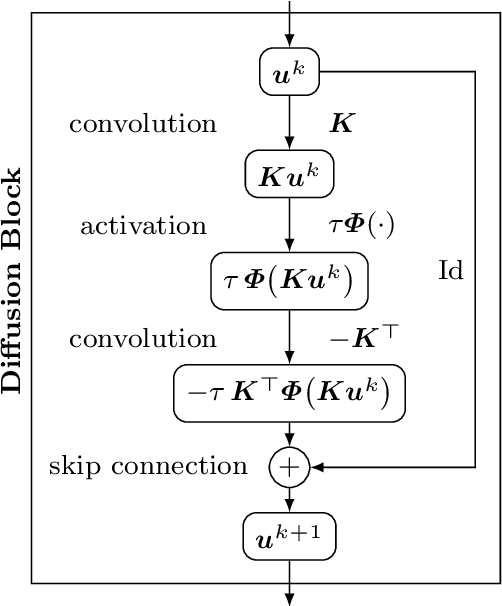
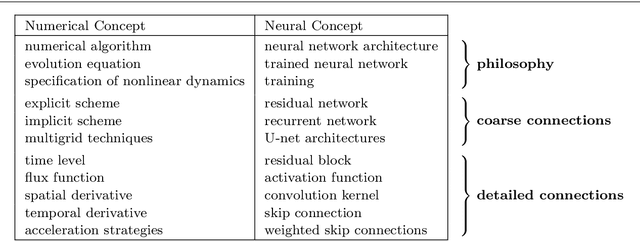
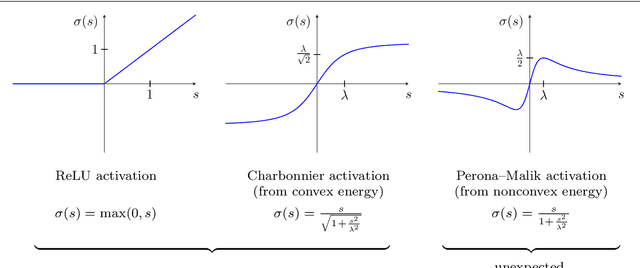
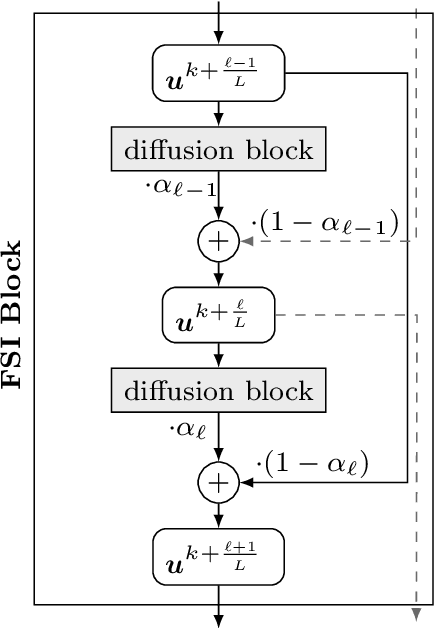
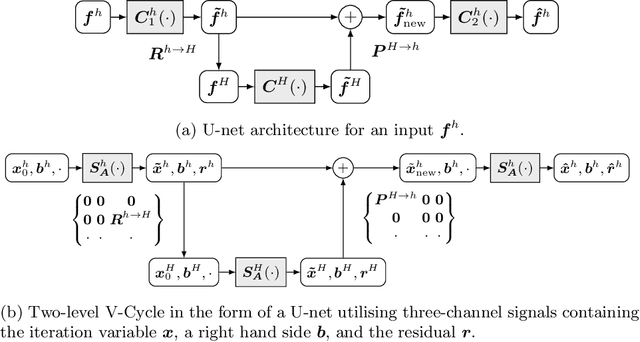
We investigate numerous structural connections between numerical algorithms for partial differential equations (PDEs) and neural architectures. Our goal is to transfer the rich set of mathematical foundations from the world of PDEs to neural networks. Besides structural insights we provide concrete examples and experimental evaluations of the resulting architectures. Using the example of generalised nonlinear diffusion in 1D, we consider explicit schemes, acceleration strategies thereof, implicit schemes, and multigrid approaches. We connect these concepts to residual networks, recurrent neural networks, and U-net architectures. Our findings inspire a symmetric residual network design with provable stability guarantees and justify the effectiveness of skip connections in neural networks from a numerical perspective. Moreover, we present U-net architectures that implement multigrid techniques for learning efficient solutions of partial differential equation models, and motivate uncommon design choices such as trainable nonmonotone activation functions. Experimental evaluations show that the proposed architectures save half of the trainable parameters and can thus outperform standard ones with the same model complexity. Our considerations serve as a basis for explaining the success of popular neural architectures and provide a blueprint for developing new mathematically well-founded neural building blocks.

Translating Numerical Concepts for PDEs into Neural Architectures

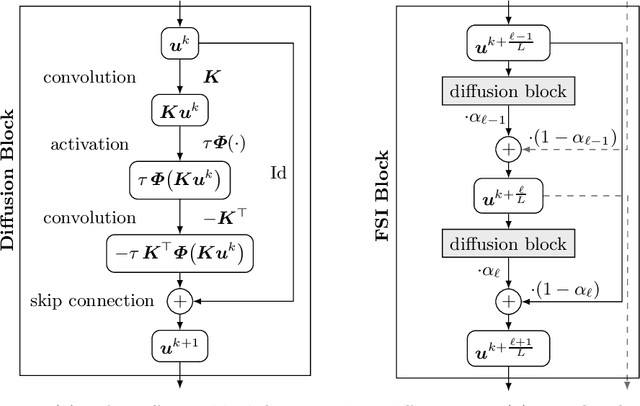
We investigate what can be learned from translating numerical algorithms into neural networks. On the numerical side, we consider explicit, accelerated explicit, and implicit schemes for a general higher order nonlinear diffusion equation in 1D, as well as linear multigrid methods. On the neural network side, we identify corresponding concepts in terms of residual networks (ResNets), recurrent networks, and U-nets. These connections guarantee Euclidean stability of specific ResNets with a transposed convolution layer structure in each block. We present three numerical justifications for skip connections: as time discretisations in explicit schemes, as extrapolation mechanisms for accelerating those methods, and as recurrent connections in fixed point solvers for implicit schemes. Last but not least, we also motivate uncommon design choices such as nonmonotone activation functions. Our findings give a numerical perspective on the success of modern neural network architectures, and they provide design criteria for stable networks.

JPEG Meets PDE-based Image Compression

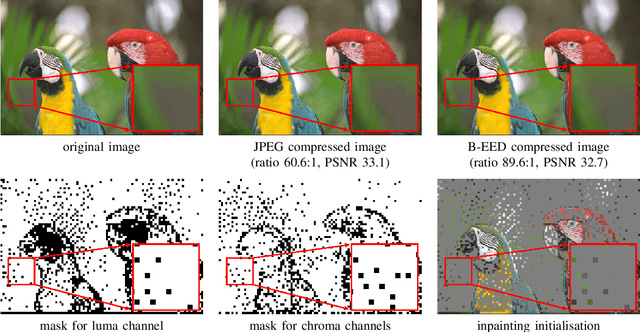
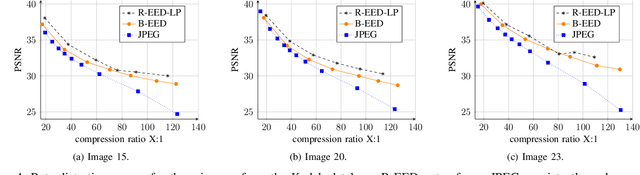
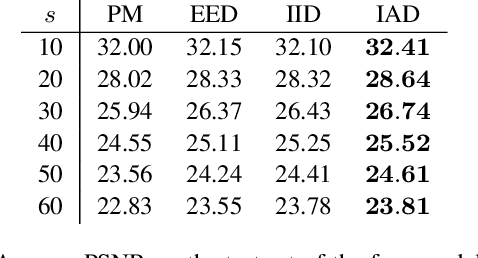
Inpainting-based image compression is emerging as a promising competitor to transform-based compression techniques. Its key idea is to reconstruct image information from only few known regions through inpainting. Specific partial differential equations (PDEs) such as edge-enhancing diffusion (EED) give high quality reconstructions of image structures with low or medium texture. Even though the strengths of PDE- and transform-based compression are complementary, they have rarely been combined within a hybrid codec. We propose to sparsify blocks of a JPEG compressed image and reconstruct them with EED inpainting. Our codec consistently outperforms JPEG and gives useful indications for successfully developing hybrid codecs further. Furthermore, our method is the first to choose regions rather than pixels as known data for PDE-based compression. It also gives novel insights into the importance of corner regions for EED-based codecs.

Learning Integrodifferential Models for Image Denoising

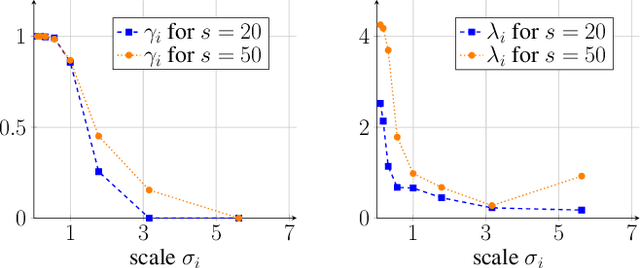
We introduce an integrodifferential extension of the edge-enhancing anisotropic diffusion model for image denoising. By accumulating weighted structural information on multiple scales, our model is the first to create anisotropy through multiscale integration. It follows the philosophy of combining the advantages of model-based and data-driven approaches within compact, insightful, and mathematically well-founded models with improved performance. We explore trained results of scale-adaptive weighting and contrast parameters to obtain an explicit modelling by smooth functions. This leads to a transparent model with only three parameters, without significantly decreasing its denoising performance. Experiments demonstrate that it outperforms its diffusion-based predecessors. We show that both multiscale information and anisotropy are crucial for its success.