Designing Rotationally Invariant Neural Networks from PDEs and Variational Methods

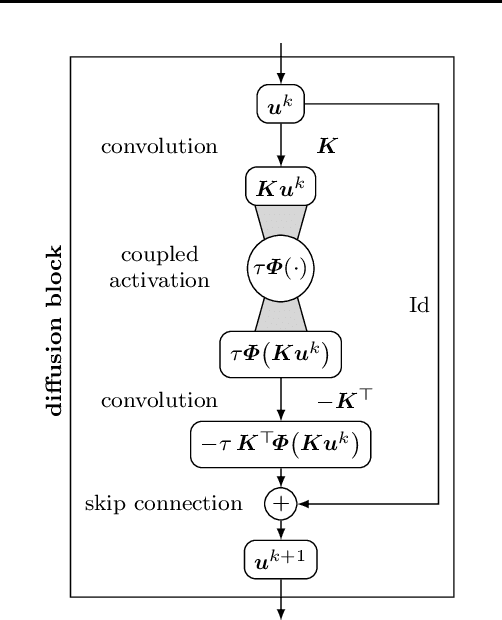
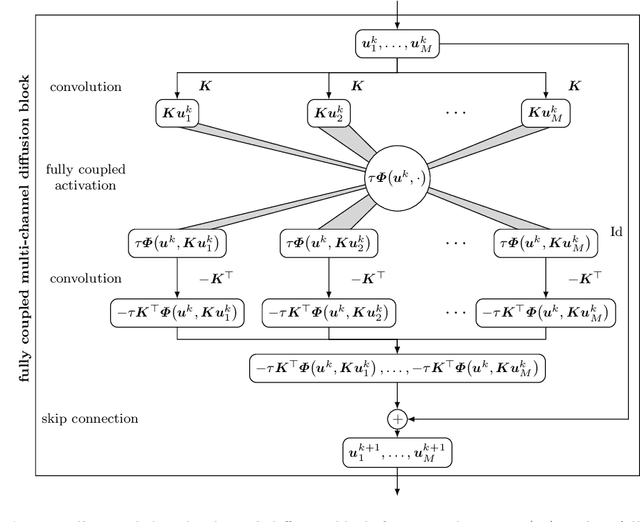
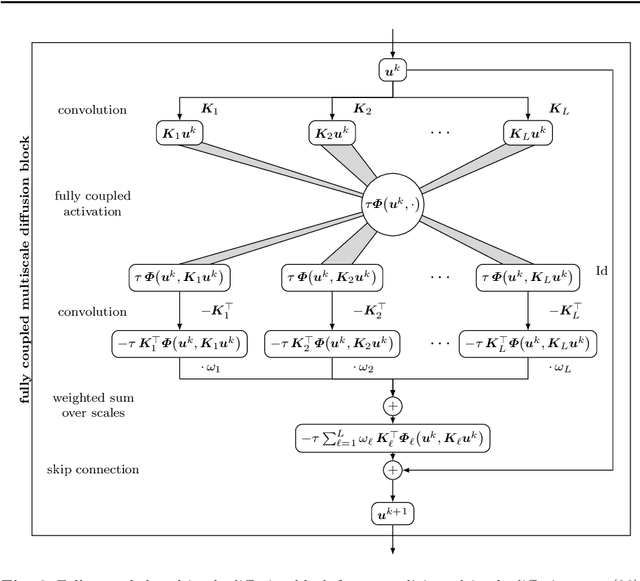
Partial differential equation (PDE) models and their associated variational energy formulations are often rotationally invariant by design. This ensures that a rotation of the input results in a corresponding rotation of the output, which is desirable in applications such as image analysis. Convolutional neural networks (CNNs) do not share this property, and existing remedies are often complex. The goal of our paper is to investigate how diffusion and variational models achieve rotation invariance and transfer these ideas to neural networks. As a core novelty we propose activation functions which couple network channels by combining information from several oriented filters. This guarantees rotation invariance within the basic building blocks of the networks while still allowing for directional filtering. The resulting neural architectures are inherently rotationally invariant. With only a few small filters, they can achieve the same invariance as existing techniques which require a fine-grained sampling of orientations. Our findings help to translate diffusion and variational models into mathematically well-founded network architectures, and provide novel concepts for model-based CNN design.

Connections between Numerical Algorithms for PDEs and Neural Networks

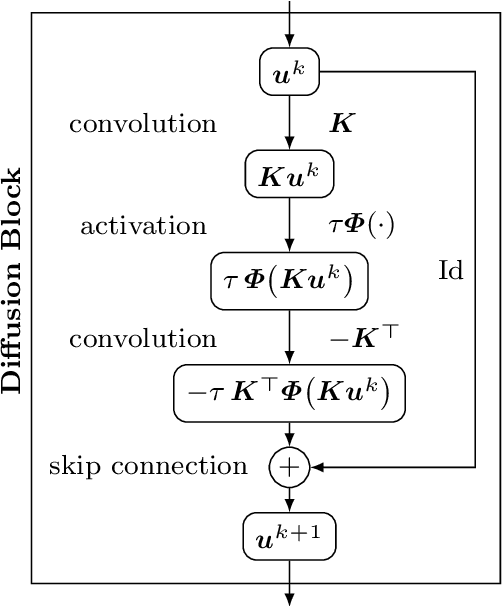
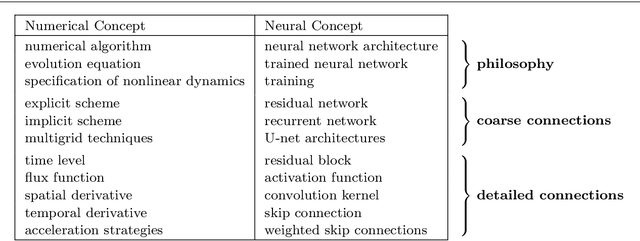
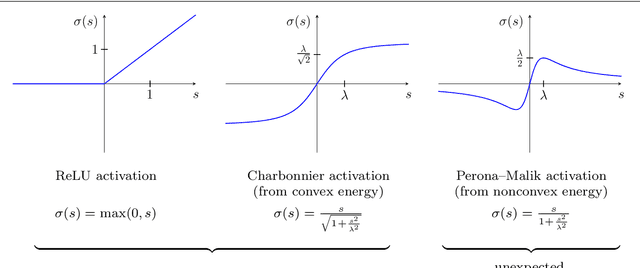
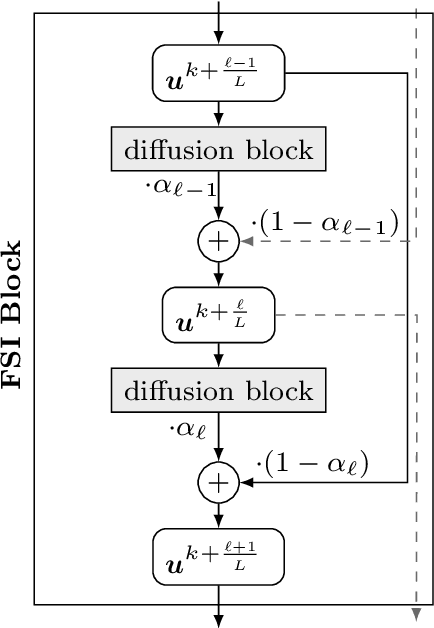
We investigate numerous structural connections between numerical algorithms for partial differential equations (PDEs) and neural architectures. Our goal is to transfer the rich set of mathematical foundations from the world of PDEs to neural networks. Besides structural insights we provide concrete examples and experimental evaluations of the resulting architectures. Using the example of generalised nonlinear diffusion in 1D, we consider explicit schemes, acceleration strategies thereof, implicit schemes, and multigrid approaches. We connect these concepts to residual networks, recurrent neural networks, and U-net architectures. Our findings inspire a symmetric residual network design with provable stability guarantees and justify the effectiveness of skip connections in neural networks from a numerical perspective. Moreover, we present U-net architectures that implement multigrid techniques for learning efficient solutions of partial differential equation models, and motivate uncommon design choices such as trainable nonmonotone activation functions. Experimental evaluations show that the proposed architectures save half of the trainable parameters and can thus outperform standard ones with the same model complexity. Our considerations serve as a basis for explaining the success of popular neural architectures and provide a blueprint for developing new mathematically well-founded neural building blocks.