SoftJAX & SoftTorch: Empowering Automatic Differentiation Libraries with Informative Gradients

Automatic differentiation (AD) frameworks such as JAX and PyTorch have enabled gradient-based optimization for a wide range of scientific fields. Yet, many "hard" primitives in these libraries such as thresholding, Boolean logic, discrete indexing, and sorting operations yield zero or undefined gradients that are not useful for optimization. While numerous "soft" relaxations have been proposed that provide informative gradients, the respective implementations are fragmented across projects, making them difficult to combine and compare. This work introduces SoftJAX and SoftTorch, open-source, feature-complete libraries for soft differentiable programming. These libraries provide a variety of soft functions as drop-in replacements for their hard JAX and PyTorch counterparts. This includes (i) elementwise operators such as clip or abs, (ii) utility methods for manipulating Booleans and indices via fuzzy logic, (iii) axiswise operators such as sort or rank -- based on optimal transport or permutahedron projections, and (iv) offer full support for straight-through gradient estimation. Overall, SoftJAX and SoftTorch make the toolbox of soft relaxations easily accessible to differentiable programming, as demonstrated through benchmarking and a practical case study. Code is available at github.com/a-paulus/softjax and github.com/a-paulus/softtorch.

AtmoDist: Self-supervised Representation Learning for Atmospheric Dynamics

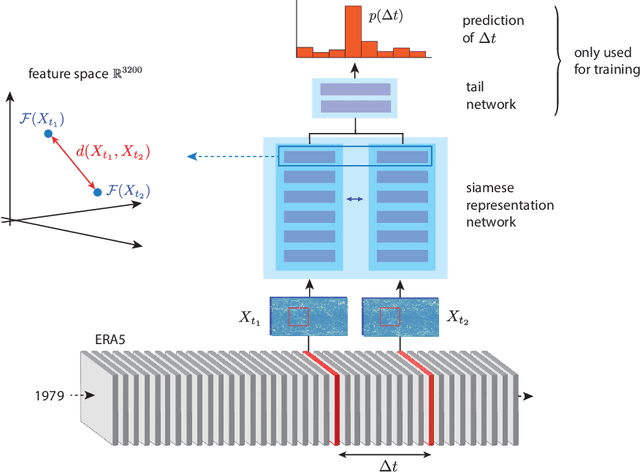
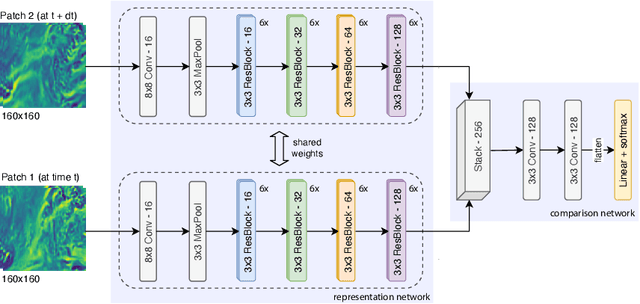
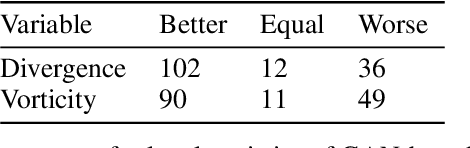
Representation learning has proven to be a powerful methodology in a wide variety of machine learning applications. For atmospheric dynamics, however, it has so far not been considered, arguably due to the lack of large-scale, labeled datasets that could be used for training. In this work, we show that the difficulty is benign and introduce a self-supervised learning task that defines a categorical loss for a wide variety of unlabeled atmospheric datasets. Specifically, we train a neural network on the simple yet intricate task of predicting the temporal distance between atmospheric fields, e.g. the components of the wind field, from distinct but nearby times. Despite this simplicity, a neural network will provide good predictions only when it develops an internal representation that captures intrinsic aspects of atmospheric dynamics. We demonstrate this by introducing a data-driven distance metric for atmospheric states based on representations learned from ERA5 reanalysis. When employ as a loss function for downscaling, this Atmodist distance leads to downscaled fields that match the true statistics more closely than the previous state-of-the-art based on an l2-loss and whose local behavior is more realistic. Since it is derived from observational data, AtmoDist also provides a novel perspective on atmospheric predictability.

Towards Representation Learning for Atmospheric Dynamics

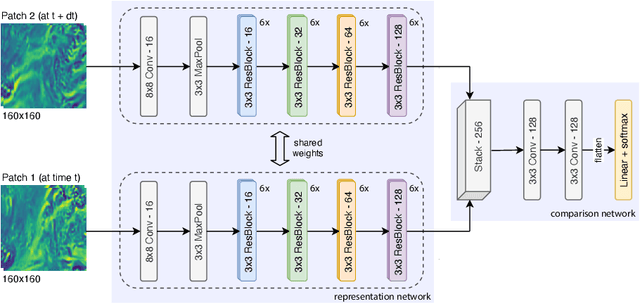
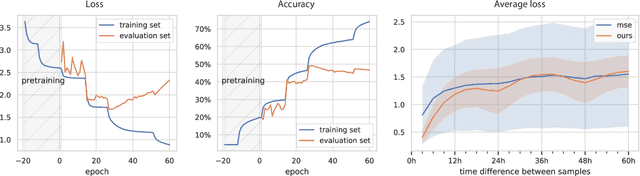
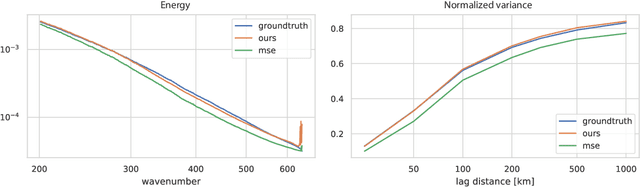
The prediction of future climate scenarios under anthropogenic forcing is critical to understand climate change and to assess the impact of potentially counter-acting technologies. Machine learning and hybrid techniques for this prediction rely on informative metrics that are sensitive to pertinent but often subtle influences. For atmospheric dynamics, a critical part of the climate system, the "eyeball metric", i.e. a visual inspection by an expert, is currently still the gold standard. However, it cannot be used as metric in machine learning systems where an algorithmic description is required. Motivated by the success of intermediate neural network activations as basis for learned metrics, e.g. in computer vision, we present a novel, self-supervised representation learning approach specifically designed for atmospheric dynamics. Our approach, called AtmoDist, trains a neural network on a simple, auxiliary task: predicting the temporal distance between elements of a shuffled sequence of atmospheric fields (e.g. the components of the wind field from a reanalysis or simulation). The task forces the network to learn important intrinsic aspects of the data as activations in its layers and from these hence a discriminative metric can be obtained. We demonstrate this by using AtmoDist to define a metric for GAN-based super resolution of vorticity and divergence. Our upscaled data matches closely the true statistics of a high resolution reference and it significantly outperform the state-of-the-art based on mean squared error. Since AtmoDist is unsupervised, only requires a temporal sequence of fields, and uses a simple auxiliary task, it can be used in a wide range of applications that aim to understand and mitigate climate change.

Optimising Spatial and Tonal Data for PDE-based Inpainting

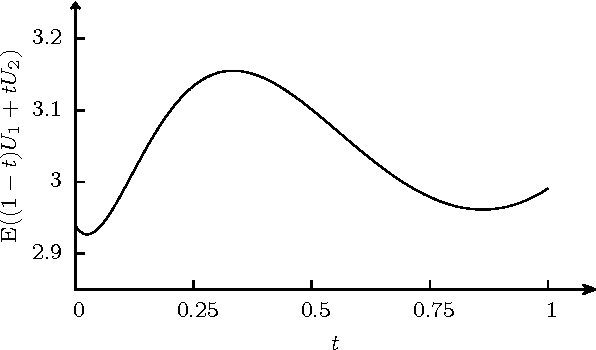
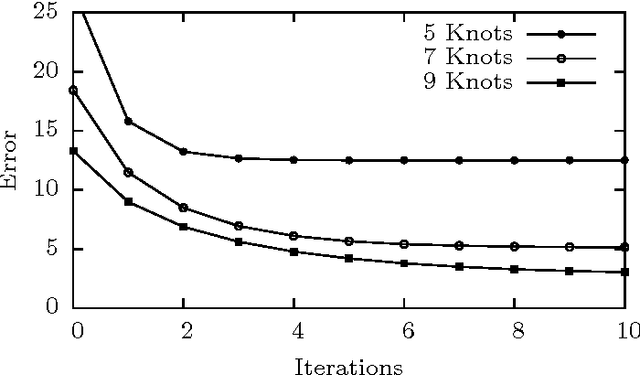
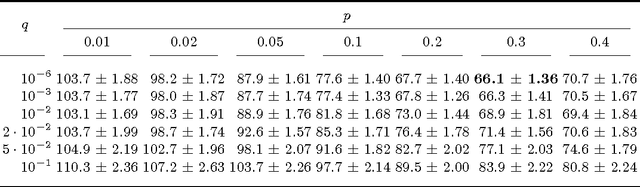
Some recent methods for lossy signal and image compression store only a few selected pixels and fill in the missing structures by inpainting with a partial differential equation (PDE). Suitable operators include the Laplacian, the biharmonic operator, and edge-enhancing anisotropic diffusion (EED). The quality of such approaches depends substantially on the selection of the data that is kept. Optimising this data in the domain and codomain gives rise to challenging mathematical problems that shall be addressed in our work. In the 1D case, we prove results that provide insights into the difficulty of this problem, and we give evidence that a splitting into spatial and tonal (i.e. function value) optimisation does hardly deteriorate the results. In the 2D setting, we present generic algorithms that achieve a high reconstruction quality even if the specified data is very sparse. To optimise the spatial data, we use a probabilistic sparsification, followed by a nonlocal pixel exchange that avoids getting trapped in bad local optima. After this spatial optimisation we perform a tonal optimisation that modifies the function values in order to reduce the global reconstruction error. For homogeneous diffusion inpainting, this comes down to a least squares problem for which we prove that it has a unique solution. We demonstrate that it can be found efficiently with a gradient descent approach that is accelerated with fast explicit diffusion (FED) cycles. Our framework allows to specify the desired density of the inpainting mask a priori. Moreover, is more generic than other data optimisation approaches for the sparse inpainting problem, since it can also be extended to nonlinear inpainting operators such as EED. This is exploited to achieve reconstructions with state-of-the-art quality. We also give an extensive literature survey on PDE-based image compression methods.