On the Regularising Levenberg-Marquardt Method for Blinn-Phong Photometric Stereo

Photometric stereo refers to the process to compute the 3D shape of an object using information on illumination and reflectance from several input images from the same point of view. The most often used reflectance model is the Lambertian reflectance, however this does not include specular highlights in input images. In this paper we consider the arising non-linear optimisation problem when employing Blinn-Phong reflectance for modeling specular effects. To this end we focus on the regularising Levenberg-Marquardt scheme. We show how to derive an explicit bound that gives information on the convergence reliability of the method depending on given data, and we show how to gain experimental evidence of numerical correctness of the iteration by making use of the Scherzer condition. The theoretical investigations that are at the heart of this paper are supplemented by some tests with real-world imagery.

Optimisation of photometric stereo methods by non-convex variational minimisation

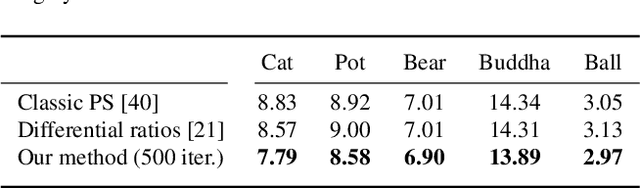
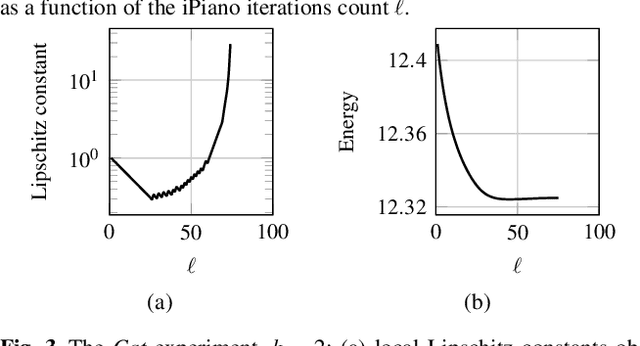
Estimating shape and appearance of a three dimensional object from a given set of images is a classic research topic that is still actively pursued. Among the various techniques available, PS is distinguished by the assumption that the underlying input images are taken from the same point of view but under different lighting conditions. The most common techniques provide the shape information in terms of surface normals. In this work, we instead propose to minimise a much more natural objective function, namely the reprojection error in terms of depth. Minimising the resulting non-trivial variational model for PS allows to recover the depth of the photographed scene directly. As a solving strategy, we follow an approach based on a recently published optimisation scheme for non-convex and non-smooth cost functions. The main contributions of our paper are of theoretical nature. A technical novelty in our framework is the usage of matrix differential calculus. We supplement our approach by a detailed convergence analysis of the resulting optimisation algorithm and discuss possibilities to ease the computational complexity. At hand of an experimental evaluation we discuss important properties of the method. Overall, our strategy achieves more accurate results than competing approaches. The experiments also highlights some practical aspects of the underlying optimisation algorithm that may be of interest in a more general context.